如何理解深度图匹配算法CIE-H？

一句话解释

CIE-H是基于深度学习技术的图匹配算法，其主要思想为通过特殊神经网络模块CIE融合图结构信息到点Embedding向量，使用基于Hungarian Attention的损失函数训练以后，可以使得传统的匈牙利算法充分考虑图结构信息，实现更好的图匹配效果。

整体流程

首先，我们可以根据下图简单了解一下算法的整体架构。首先，对于两张待匹配的图片，我们可以根据CNN网络得到目标点的Embedding向量，同时可以根据Gaussian Kernel根据点的Embedding向量得到边的Embedding向量。

随后，我们就可以直接使用图神经网络提取高阶点特征和边特征。图神经网络更新公式如下所示，其中 H^{l+1} 代表 l+1 阶点特征。可以看到，该特征由低阶的点特征 H ，边特征 E ，邻接矩阵 A ，和参数矩阵 W_0 共同得到。边特征 E^{l+1} 也是同理，只不过采用了 W_1 参数矩阵。

为了促进图匹配算法的计算，作者进一步计算了不同图之间的点相似性 M_{i,j} ，并在此基础上使用Sinkhorn算法得到了Doubly-Stochastic Matrix。 M_{ij} 矩阵的计算方式也比较简单，主要利用两张图的点特征 H_{(1)} 和 H_{(2)} ，同时利用一个可训练的参数矩阵 \wedge 进行变换。

随后，Sinkhorn算法过程如下所示。从实际意义上来说，这个算法是古圣先贤研究出来的可以微分的，模拟匈牙利图匹配算法的算法。可以看出，该算法是一个迭代的过程，即重复使用 M 矩阵进行变换。最终得到的结果矩阵就近似于采用匈牙利算法得到的图匹配矩阵。

在图神经网络信息融合的过程中，作者还使用了跨图信息融合以促进两张待匹配图之间的信息融合。具体融合方式如下所示，即第 l 层图神经网络的点Embedding向量 H_{1}^l 与另一张图的点Embedding向量 H_2^l 进行拼接，然后使用一个神经网络 f_c 对信息进行融合。

Channel-Independent Embedding

传统的匈牙利算法只能考虑点匹配信息，如果需要考虑边匹配信息，那么整个问题将会是一个NP-Hard的问题。为了解决这个问题，作者提出了一个Channel-Independent Embedding（CIE）模块，用以融合边信息到点Embedding向量中。

在计算出点Embedding向量 H 之后，我们来看一下如何将点Embedding向量 H 和边Embedding向量 E 进行融合。首先，我们来看一下传统的融合方式。如下公式所示， w 代表 v 的所有邻居节点， H_w^l 代表点 w 的第 l 阶Embedding向量。从下面公式中可以看出，传统GCN融合边信息的方法，实际上就是边Embedding向量 E_{vw} 经过一个神经网络 f_t 变换之后，与点Embedding向量 H_w^l 相乘。最终再使用 u_t 神经网络融合上节点 v 本身的特征向量 H 之后，可以构成最终的点Embedding向量 H_v^{l+1} 。

值得一提的是，这里的边融合神经网络 f_t 的选择非常关键，也是目前基于深度学习的图匹配算法的性能瓶颈所在。使用传统的全连接层会导致较高的参数量，从而导致较高的计算复杂度和训练难度。

为了缓解上述问题，作者提出了Channel-Independent Embedding（CIE）模块。公式如下所示，其中 \Gamma_{\mathrm{N}}(\cdot \circ \cdot) 代表了channel-wise operator。具体来说，一个大小为 m*k 的点Embedding矩阵 H^l ，可以通过一个线性变换层，映射为一个 n*k 的矩阵。而对于一个大小为 m*k*k 的边Embedding矩阵 E^l ，也可以通过一个线性变换层，映射为一个 n*k*k 的矩阵。Channel-wise操作的核心思想是，直接利用上述变换后矩阵进行卷积操作。

直观来理解的话，可以认为线性变换层的作用是对Channel方向进行聚合，即将 m 个Channel聚合为 n 个Channel。在每个Channel上，大小为 k*k 的边Embedding矩阵和大小为 k 的点Embedding向量进行乘法操作，最终可以得到一个大小为 k 的点Embedding向量。

有了上面的思想，作者也同时将边Embedding向量 E_{vw} 的计算方式进行了类似的修改。这里也是每个Channel独立进行矩阵乘法操作，最终得到边Embedding向量 E 。

具体来说，上述过程的更新公式也可以用下面两个公式来表示。第一个公式代表了点向量 H 的更新方式，可以看到变换后的边向量 WE 首先和邻接矩阵 A 进行一个Element-wise Product操作，随后再和变换后的点向量 WH^l 。最终，我们将得到的矩阵和原始的点向量矩阵 WH^l 相加，就可以得到最终的点向量矩阵 H^{(l+1)} 。边Embedding向量 E^{l+1} 的计算方式也是类似的，只不过这里使用了 pairwise difference计算点与点Embedding向量的差，随后与边Embedding向量进行Element-wise Product操作，最终加上原始的边Embedding向量 E^{l} ，最终实现图神经网络的聚合操作。

如何理解上述这个过程呢？作者给出一个比较直观的解释，即我们可以将上述过程视为类似Separable Convolution的过程。如果我们使用的是传统的 f_t 函数，那可能就需要一个比较复杂的 f_t 函数，使得转换后的 f_t(E_{vw})H_w 具有足够多的信息量。而这里作者提出的CIE模块，相当于是将上述复杂的 f_t 模块拆分为两个线性模型 W_1 和 W_2 。这两个线性模块分别对 E_{vw} 和 H_{w} 进行变换，从而可能具有更好的预测性能。

Hungarian Attention

整体来说，算法的整体流程可以用下图来描述。即首先图神经网络可以得到点的Embedding向量，向量之间可以计算Similarity Matrix。之后，我们可以使用Sinkhorn算法模拟执行匈牙利算法，得到Double-Stochastic Matrix。对于传统的深度图匹配算法，到这一步之后就可以通过匈牙利算法基于Double-Stochastic Matrix得到最终的结果。

传统Deep Graph Matching方法一般采用Cross Entropy作为损失函数，即要求最终Sinkhorn算法求解得到的矩阵 S 和标注匹配方案 S^G 越接近越好。

但是这种损失函数和我们最终在测试阶段所使用的策略是不一致的。因为，最终我们在测试阶段是使用匈牙利算法根据整个矩阵找到最大匹配。具体来说，如果最终阶段使用的是匈牙利算法基于Double-Stochastic Matrix求解最终的匹配方案，实际上我们并不需要在训练阶段让Double-Stochastic Matrix和最终匹配解完全一致。强行追求一致性可能反而会导致模型训练困难。

为了解决这个问题，作者提出了Hungarian Attention机制。首先可以通过匈牙利算法求解出当前Double-Stochastic Matrix方案下匹配解 P ，然后与真实的Ground-Truth Matrix Q 作比较。最终的注意力矩阵 Z 为 P 和 Q 的并集，即 P \cup Q 。

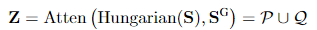
基于Hungarian Attention机制的最终损失函数如下所示。从公式中可以看出，采用Hungarian Attention机制之后，最大的不同在于仅仅考虑了一个小区域的输出值。而那些匈牙利算法涉及不到的部分，在最终损失函数计算这一步不再进行考虑。基于这样一种机制，我们就可以大大减轻模型优化的复杂度。

实验结果

从最终的实验结果来看，Hungarian Attention机制具有明显的效果。如下图所示，使用Hungarian Attention Loss最终可以得到比使用Permutation Loss更好的结果。

从数值结果来看的话，CIE模块+Hungarian Attention机制最终可以得到在Pascal VOC这个图匹配测试集上达到最佳的模型预测性能，进一步验证了算法的有效性。值得一提的是，灰色部分展示了模型的训练准确率，即从图中可以看出，传统算法PCA-P在训练集上出现了过拟合的问题，而CIE-P算法则相对表现良好。

论文总结

这篇论文的整体思路还是相对清晰的，即利用CIE模块替代传统的GCN网络，用以更高效的提取图特征以辅助图匹配任务，同时设计了Hungarian Attention损失函数以缓解传统损失函数优化困难的问题。对于深度图匹配的研究者来说，这篇文章是一篇非常值得阅读的文章。