Formule pour la distance entre deux points (géométrie)

Sur cette page, vous trouverez comment calculer la distance entre deux points en géométrie (formule). Vous pourrez également voir des exemples et, en plus, pratiquer avec des exercices résolus de la distance entre deux points.

Quelle est la formule de la distance entre deux points ?

La distance entre deux points est égale à la longueur du segment qui les joint. Par conséquent, en mathématiques, pour déterminer la distance entre deux points différents, il faut calculer les carrés des différences entre leurs coordonnées puis trouver la racine de la somme desdits carrés.

Autrement dit, la formule utilisée pour calculer la distance entre deux points différents sur le plan cartésien est la suivante :

Soit les coordonnées de deux points distincts :

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

La formule de la distance entre deux points est :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Cette formule vient de la grandeur d’un vecteur. En fait, ce que nous faisons avec cette formule calcule en fait la magnitude du vecteur qui est déterminé par les deux points en question. Vous pouvez en savoir plus à ce sujet dans l’explication de ce qu’est le module d’un vecteur .

D’autre part, en géométrie analytique la démonstration de la formule de la distance entre deux points peut aussi se faire à partir du théorème de Pythagore :

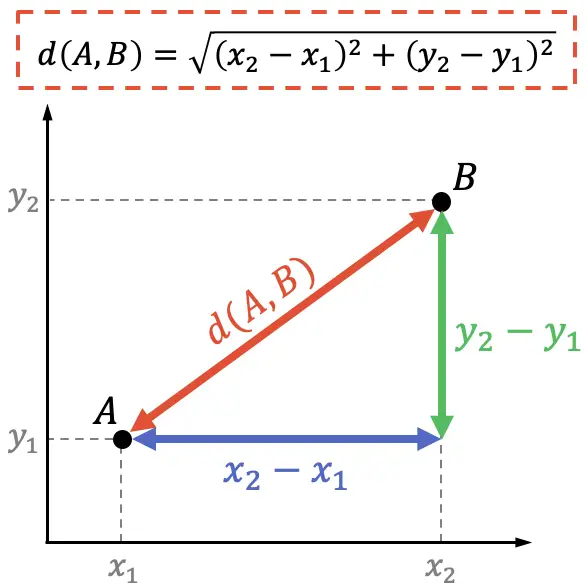
Le théorème de Pythagore dit que le carré de l’hypoténuse d’un triangle rectangle est équivalent à la somme des carrés de ses jambes, donc :

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

Et pour obtenir la formule il suffit de dégager la distance entre les 2 points :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Enfin, il convient de noter que, si nous travaillions avec des points à 3 coordonnées, la formule de la distance entre deux points dans l’espace (dans R3) serait la même mais en ajoutant la coordonnée Z :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

Exemple de calcul de la distance entre deux points

Une fois que nous avons vu la définition de la formule de la distance entre deux points, voyons maintenant comment déterminer ladite distance à l’aide d’un exemple :

Trouver la distance entre les deux points suivants :

$A(-1,7) \qquad \qquad B(3,4)$

Pour trouver géométriquement la distance entre les deux points, il suffit d’appliquer la formule :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Maintenant, nous substituons les coordonnées des points dans la formule :

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

Et on fait les calculs :

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

La distance entre les deux points est donc égale à 5 unités.

Évidemment, la valeur de la distance doit toujours nous donner un signe positif, car les distances sont toujours positives. Sinon, cela signifie que nous avons fait une erreur dans une étape.

Résolution des problèmes de distance entre deux points

Exercice 1

Calculez la distance entre les deux points suivants :

$A(4,2) \qquad \qquad B(1,5)$

voir solution

Pour trouver la distance géométrique entre les deux points, il suffit d’utiliser la formule :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Maintenant, nous substituons les coordonnées des points dans la formule :

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

Et on fait les calculs :

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

Exercice 2

Trouver la distance entre les deux points suivants :

$A(8,6) \qquad \qquad B(-4,1)$

voir solution

Pour trouver la distance mathématique entre les deux points, nous devons utiliser la formule correspondante :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Maintenant, nous substituons les coordonnées des points dans la formule :

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

Et on fait les calculs :

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

Exercice 3

Calculer le périmètre du triangle formé par les points A, B et C représenté graphiquement ci-dessous :

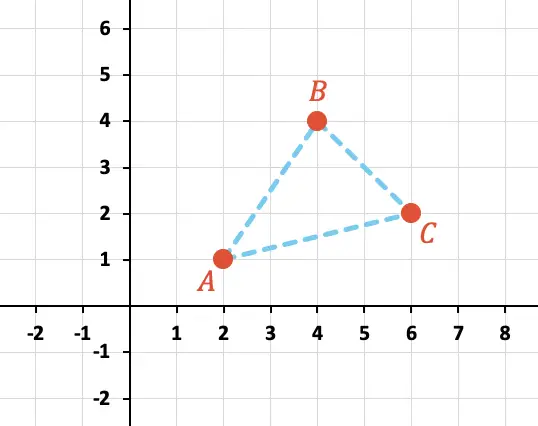
exercice résolu de la distance entre deux points

voir solution

Tout d’abord, nous devons identifier les coordonnées X et Y de chaque point sur le graphique :

$A(2,1)$

$B(4,4)$

$C(6,2)$

Et maintenant, nous devons calculer la distance entre tous les points avec la formule :

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

Donc le périmètre du triangle sera la somme de la longueur des 3 côtés :

$P=3,61+4,12+2,83= \bm{10,56}$

Exercice 4

Vérifier si le triangle dont les sommets sont les points A, B et C est un triangle isocèle. Soit les trois points :

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

voir solution

Pour qu’un triangle soit isocèle, il faut que deux de ses côtés soient égaux. Il faut donc trouver la longueur de chacun de ses côtés, qui correspondent aux distances entre ses sommets.

On calcule donc la distance entre les sommets du triangle :

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

Pour que le triangle ait 2 côtés identiques et que le troisième côté mesure différemment des deux autres, il s’agit donc effectivement d’un triangle isocèle.

Exercice 5

Trouvez un point sur l’axe Y qui est équidistant des deux points suivants :

$A(5,-3) \qquad \qquad B(-2,4)$

voir solution

Tout d’abord, si le point est situé sur l’axe des ordonnées (axe OY) cela signifie que l’abscisse du point est nulle :

$P(0,y)$

Deuxièmement, si le point est équidistant des points A et B, cela implique que l’équation suivante est remplie :

$d(P,A)= d(P,B)$

Ainsi, en utilisant la formule de la distance entre deux points, nous pouvons trouver la valeur de la variable y à partir de l’équation précédente :

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

Puisque les deux côtés de l’équation ont une racine, nous pouvons les simplifier :

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

On résout les puissances et les égalités notables (ou produits notables) :

$25+9+y^2+6y=4+16+y^2-8y$

Et on opère jusqu’à trouver la valeur de l’inconnue y :

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

En bref, le point que l’énoncé du problème nous a demandé est :

$\bm{P(0,-1)}$

Si cet article vous a été utile, vous serez probablement également intéressé par des exercices sur la distance entre un point et une droite . Sur la page liée, vous trouverez non seulement des exercices résolus étape par étape, mais également une explication détaillée du calcul de la distance entre les points et les lignes, des exemples et l’application de la formule de la distance entre un point et une ligne pour déterminer un autre type de distance.

Quelle est la formule de la distance entre deux points ?

Exemple de calcul de la distance entre deux points

Résolution des problèmes de distance entre deux points

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply