MAML算法,model-agnostic metalearnings?
13 个回答
MAML这个算法最大的优势在于他是要处理什么就向着什么学习。这种简单直观粗暴的方法让他成了一种非常实用而且可以解决各种类型task的通用型算法。
楼上有人举的例子挺形象的。我们现在来看一下它的算法思路。
首先你需要理解是什么task?task可以是一个5分类问题,可以是拟合一个三角函数,可以是强化学习里面某一系列动作决策。都说meta learning 其实是学习一种规则,然后learner可以根据meta learner学习得到的规则快速应用到某个适应的问题或场景中。其实,MAML学习的就是初始化参数的规则。这个初始化的参数θ在参数空间中具有对每个任务最优参数解θ1,2,..n的高度敏感(其实就是梯度方向垂直),使其能够在一步Gradient Descent中沿着梯度方向快速达到最优点。
在这里我们一定要理解参数空间,和特征空间类似,参数可以看做更高维度的一个向量,那么每个模型对应的参数(Conv层,linear层的kernel所构成的learnable parameters) 在参数空间中其实就是一个点。每一次迭代优化,都导致了在这个参数空间里位置的改变。

那么如何学习这种能力,或者说规则呢?这里MAML采取的方式是优化参数在各个任务上的梯度方向矢量和。具体原理则是元任务adapt一步(或几步)提供的二阶导信息,也就是curvature of tasks,这样的高阶导信息可以为模型的初始化提供方向信息,也就是我们所用的每个task的梯度方向。优化分为两层: inner loop和outer loop。Inner loop就是training procedure,对于每个任务学习处理这个任务的基本能力。outer loop就是meta training procedure,学习多个任务的泛化能力。
我们以这篇paper要解决的首要问题few-shot learning 为例(施主你那个图看不清):

首先看第1行,初始化模型参数,不必多说。
第3行,开始sampling tasks,每个task其实就是一组样本,这组样本里面包含N个类,每类K个训练样本,K'个测试样本。之所以叫做任务样本,是因为这N个类总是不同的类别信息,比如第一次{1,3,4,5,2},第二次{3,6,7,8,9}。对于每个任务,比如5类,每类三个样本,我们还需要进一步进行划分: 每类1个样本train,2个样本来validate,此时这5x1个样本集叫做 training set(也叫5-way 1-shot learning task),后面5x2个样本集叫做 test set。meta training和meta-testing包含不同的class。

第4行, 进入inner loop。
第5,6行,在我们采样的task batch中的第i个task(Ti)的meta training set 上计算一步gradient descent,为啥要这样捏?因为这个时候你只做了一步GD,你会朝这个任务的参数最优解仅仅迈出一步(注意MAML要学习的就是这种能力),而此时,如果你直接反传,继续优化,你的model参数就沿着这个专一的任务越走越远了。对于task Ti而言,我们先用meta training set去获得原模型参数θ在Ti上的training loss L(Ti, θ)。利用GD的公式得到θi =θ - lr*d{loss L(Ti, θ)}/dθ, lr是inner loop learning rate, 此时计算他在这个task上的期望参数θi,这个参数仅仅用作期望,不用更新model原始的真实参数θ。至于朝每个task Ti优化地好不好,loss多少,用Ti里的validation set 在期望参数θi上去validate。从而得到了一个新的loss, meta loss L'(Ti, θi)。这里只能看做是meta loss的一部分,整个inner loop计算出来的sum of L'(Ti, θi)才是最后的meta loss。具体实现上,我们可以拷贝一份当前的参数去计算期望参数,然后再去计算meta loss。
第8行,outer loop的更新(meta training procedure),由于我们采样了一批任务,然后我们又耐心地计算了每个任务的期望参数,然后基于期望参数去validate了,得到了Sum of {task-specific loss L'(Ti, θi)},这有什么用呢?

它之所以叫做meta loss的原因而不叫做training loss的原因在于它的反传方式,我们求和了所有的loss却不在期望参数上反传,而是用这个meta loss在model原来的参数θ上求导(公式求导算子的下标注意!重点,必考!),然后再优化model的参数。这里对于θ求导的时候,我们其实得到了二阶导信息,不信请看:

说白了期望参数就是每个任务上的配角大佬,我们的主角按照他们提供的经验成长,最后拿奖的时候跟他们没啥关系,因为从新手村的任务到最后打大boss,整部影片经历了无数的配角,最后你连名字都忘记了(这个临时大佬用完就被释放了),但是你从这些人中学习得了各种各样的“初始化”技能。
这样设计的好处是你不断在参数空间中寻找一个奇点位置(这个位置不对应任何任务的最优解)最终收敛,但是这个位置却神奇地对应着很多任务最优解的最近处。用这个位置给模型进行初始化以后,具备朝任何一个给定的task最优参数的位置快速前进(只优化一步)的能力。更本质一点对MAML的理解:
假设我们需要找到一个点,距离所有的task最优解最近,我们会选择什么方案? 很明显,这里有两种方案,1)Meta Learning scheme: 我们让learner自己找task的梯度,然后找折中的优化方向。最后的model是需要做finetune到某个特定的task最优解。 2) Task-wise training scheme: 我们面向所有的task求各自的梯度,然后把他们加起来。最后的model就是直接在新task上做inference而不需要finetune。Intuitively, 我们采取的方案2 试图找到一组parameters θ* 使得对所有的任务都performance最好,显然,同一个分类器不可能做到这么牛X的事情。反之,方案1 采取的策略会更加明智,找到一组当前对所有task都performance不好的最优解θ*,我允许最优解出现在θ*周围更大半径内,而又不距离太远,这样,稍做几步gradient descent就可以达到最优解。下图给出了以一个简单的例子在假设parameter分布的一个manifold上。z坐标表示loss,水平坐标系表示解空间。方案1 更可能分布在一个peak上,被每个task最优解围绕,容易收敛到最优解。 方案2 更像右图,试图找到一个单一解对所有task的泛化性能最好。

再说几点MAML存在的弊端:
- Hard to train: paper中给出的backbone是4层的conv+1层linear,试想,如果我们换成16层的VGG,每个task在算fast parameter的时候需要计算的Hessian矩阵将会变得非常大。那么你每一次迭代就需要很久,想要最后的model收敛就要更久。
- Robustness一般:不是说MAML的robustness不好,因为也是由一阶online的优化方法SGD求解出来的,会相对找到一个flatten minima location。然而这和非gradient-based meta learning方法求解出来的model的robust肯定是没法比的。
好,说完了算法,说一下细节部分,为什么这个地方是两个学习率,要知道,为了一步优化探测task最优参数的位置,我们必须使用稍微大点的学习率,这叫一步到位。而优化你真正模型参数的学习率应该是很小的,因为他必须在参数空间中经过漫长的迭代,慢慢找到最合适的位置。
对于回归task而言,应用上面提到的算法,只是task 的form不一样而已,比如我们需要回归出一个sin函数,那么快速学习的标志就是,我只给你5个点你能快速拟合出这条直线。所以paper后面也是给出他只做一步优化所得到的拟合效果,是显然好于finetune的方法的。
----------------------------------------2019年8月9号----------------------------------------
感谢细心的网友,二阶求导图里的公式已更正
----------------------------------------2022年3月24号----------------------------------------
感谢还在关注这个meta learning领域的大佬们,时隔这么久,我又来考古(广告)了。对于和我一样想进一步弄清楚meta learning理论机制的朋友,这里给大家share一下我们在简单的Linear Model下理论分析的思路。
假设我们只关心MAML和我们前面提到的task-wise(也就是ERM)有什么不同。考虑在一个mixed linear regression problem上(为了简单,考虑convex case,也就是不考虑learning rate带来的影响以及多local minima的复杂情况。当然,文章里有把results拓展到overparameterized model),两种算法带来的global minima有什么区别,进而希望理解MAML的优化行为。
对于这个问题,文章主要给出两个结论。
- 通过分析向每个task做adaptation的学习率,我们发现最优学习率(使得MAML objective funtion最小)其实implicitly的depends on the inverse of data variance。所以从统计上来说,一个dataset的variance在某种程度上决定了MAML应该采用什么样的adaptation step size。
- 从几何上分析,我们发现和ERM相比,即使MAML使用非常小的adaptation learning rate,它所学到的meta initialization依然有着“距离所有task optima更小”的性质。这在一定程度上证明了大家empirically认为MAML converges to the vicinity of task optima的statement。在文章的setting中,MAML的meta initialization向一个task adapt任意步的期望distance总小于ERM。这也因此给MAML带来了fast adaptation的优势。可能pre adaptation phase,MAML的loss要比ERM还差,但是随着adaptation的进行,MAML很快就逆转了劣势,取得了更低的test loss(refer to Figure 5)。
最后,论文的linear setting也过于简单,而且假设也too strong,后续还有很多改进的地方。希望感兴趣的大佬能继续推进我们的工作。
具体的可以参照论文,地址:
我们先从Meta Learning的概念说起。
原始的机器学习的流程被认为是下面这这样的:

也就是我们根据我们先验知识设计网络架构和参数初始化方法,从Training Data中得到参数的梯度,使用一阶条件调整参数。
因为网络架构已经是提前设计好的,我们学习的最终输出其实就是参数。

图中红框内的都是人类之前设计好的,Meta Learning的目标就是学习这些是如何设计的。
Meta Learning的任务是输入,现阶段成熟的方法一般默认这些任务是同类的。例如图像分类。
输入的训练集可以是十个图像分类任务,这些任务有自己的训练集和测试集,但是我们在这里称为Support set和Query set。
而测试集可以是两个额外的任务,当然他们也有自己的Support set和Query set。
Machine Learning的训练和测试数据如下:

Meta Learning的训练和测试数据如下:

在Machine Learning中我们定义损失函数为 l = L(f) , f 表示这个模型,损失函数 L 是一个泛函,通常我们用测试数据经过模型的输出和原来的label的差异作为损失函数的估计。
而Meta Learning中,我们用这些 l 的和估计Meta Learning的损失:
L(F)=\sum_{n=1}^{N} l^{n}
在Meta Learning中,我们常用Omniglot作为数据集训练,Omniglot有1623个characters,每个character有20个examples。
characters如下:

而examples指的是同样一个character经过不同的人写出来的结果:

Mate Learning的任务被称为N-ways K-shot classification,N指的是有多少个类别,K指的是每个类别有多少个sample。
Meta Learning常常和Few-shot Learning一起出现,Few-shot Learning指的是样本特别少的Machine Learning。
例如一个20-ways 1-shot classification,就是一共有20个类别,每个类别只有一个训练样本。往往这样的问题用传统的Machine Learning是很难解决的。20-ways 1-shot classification的一个例子如下:
Support set:
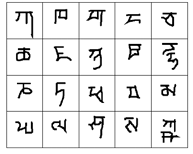
Query set:

因为Few-shot Learning每个任务的训练数据非常少,我们希望用Meta Learning学习出这类任务(例如都是分类任务)的共性,以此来提升表现。
从整个Omniglot数据集中,我们sample出多个每组20个characters的子集,每个character sample1个example,就可以将他们作为多个20-ways 1-shot classification任务,形成Meta Learning的训练数据了。
而MAML就是一种决定如何初始化参数的方法。
它默认要求了不同任务的网络模型是一样的,更确切的说,它没有“根据训练集生成初始化参数”的能力,它对所有任务的初始化参数是相同的。
也就是说,它其实是找到了对于所有的任务,最好的一种参数初始化的方法。并让所有任务都按照这种方法进行参数初始化。
这当然要求模型的结构是相同的了,不然根本没有办法使用同样的参数。
我们设初始化的参数为 \phi ,每个任务的模型一开始的参数都是 \phi ,经过训练后,参数就会变成 \hat{\theta}^{n} ,而用 l^{n}\left(\hat{\theta}^{n}\right) 表示每个任务的损失。
那么,对于这个Meta Learning而言,整体的损失函数应该是 \phi 的函数:
L(\phi)=\sum_{n=1}^{N} l^{n}\left(\hat{\theta}^{n}\right)
当然如果我们把 \phi 看作参数, L 就是函数,把 \phi 看作函数, L 就是泛函,不过问题不大。
而对于单一的一个任务而言, \phi 被视为超参数。
回忆一下我们之所以能很有效的调节参数,而没办法高效的调节超参数,就是因为我们没办法计算超参数的梯度,而MAML则是基于一些假设,使我们可以计算 \phi 的梯度。
一旦我们可以计算 \phi 的梯度,就可以直接更新 \phi :
\phi \leftarrow \phi-\eta \nabla_{\phi} L(\phi)
而所谓的假设即是:每次训练只进行一次梯度下降。
这个假设听起来不可思议,但是却也有一定的道理,首先我们只是在Meta Learning的过程中只进行一次参数下降,而真正学习到了很好的 \phi 之后自然可以进行多次梯度下降。

只考虑一次梯度下将的原因有:
- Meta Learning会快很多
- 如果能让模型只经过一次梯度下降就性能优秀,当然很好
- Few-shot learning的数据有限,多次梯度下降很容易过拟合
- 刚才说的可以在实际应用中多次梯度下降
如果只经历了一次梯度下降,模型最后的参数就会变成:
\hat{\theta}=\phi-\varepsilon \nabla_{\phi} l(\phi)
当然因为 l 的不同,最后不同任务的 \hat{\theta} 也会不一样,准确来说应该是:
\hat{\theta}^n=\phi-\varepsilon \nabla_{\phi} l^n(\phi)
现在我们已经有 L(\phi)=\sum_{n=1}^{N} l^{n}\left(\hat{\theta}^{n}\right) ,下一步就是计算 \phi 关于 L 的梯度。
我们有:
\nabla_{\phi} L(\phi)=\nabla_{\phi} \sum_{n=1}^{N} l^{n}\left(\hat{\theta}^{n}\right)=\sum_{n=1}^{N} \nabla_{\phi} l^{n}\left(\hat{\theta}^{n}\right)
现在的问题是如何求 \nabla_{\phi} l^{n}\left(\hat{\theta}^{n}\right) ,略去上标 n ,有:
\nabla_{\phi} l(\hat{\theta})=\left[\begin{array}{c}{\partial l(\hat{\theta}) / \partial \phi_{1}} \\ {\partial l(\hat{\theta}) / \partial \phi_{2}} \\ {\vdots} \\ {\partial l(\hat{\theta}) / \partial \phi_{i}} \\ {\vdots}\end{array}\right]
注意 l 是 \theta 的函数,而 \theta 又和每一个 \phi_i 有关,因此有:
\frac{\partial l(\hat{\theta})}{\partial \phi_{i}}=\sum_{j} \frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_{j}} \frac{\partial \hat{\theta}_{j}}{\partial \phi_{i}}
也就是说,每一个 \phi_i 通过影响不同的 \theta_i ,从而影响到了 l :

l 和 \theta 的关系是很直接的,我们可以直接求 \frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_{j}} ,现在的问题是怎么求 \frac{\partial \hat{\theta}_{j}}{\partial \phi_{i}} 。
注意 \theta 和 \phi 的关系也是显然的:
\hat{\theta}=\phi-\varepsilon \nabla_{\phi} l(\phi)
把向量的形式展开:
\widehat{\theta}_{j}=\phi_{j}-\varepsilon \frac{\partial l(\phi)}{\partial \phi_{j}}
我们考虑 i \neq j :
\frac{\partial \widehat{\theta}_{j}}{\partial \phi_{i}}=-\varepsilon \frac{\partial l^2(\phi)}{\partial \phi_{i} \partial \phi_{j}}
而当 i=j :
\frac{\partial \widehat{\theta}_{j}}{\partial \phi_{i}}=1-\varepsilon \frac{\partial l^2(\phi)}{\partial \phi_{i} \partial \phi_{i}}
当然到此为止已经把梯度计算出来了,但是在MAML的论文中其实做了简化,它直接不计算二阶条件。
\frac{\partial \widehat{\theta}_{j}}{\partial \phi_{i}}=-\varepsilon \frac{\partial l^2(\phi)}{\partial \phi_{i} \partial \phi_{j}} \approx 0
\frac{\partial \widehat{\theta}_{j}}{\partial \phi_{i}}=1-\varepsilon \frac{\partial l^2(\phi)}{\partial \phi_{i} \partial \phi_{i}} \approx 1
那么原来的偏导近似为:
\frac{\partial l(\hat{\theta})}{\partial \phi_{i}}=\sum_{j} \frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_{j}} \frac{\partial \hat{\theta}_{j}}{\partial \phi_{i}} \approx \frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_{i}}
整个梯度就可以近似为:
\nabla_{\phi} l(\hat{\theta})=\left[\begin{array}{c}{\partial l(\hat{\theta}) / \partial \phi_{1}} \\ {\partial l(\hat{\theta}) / \partial \phi_{2}} \\ {\vdots} \\ {\partial l(\hat{\theta}) / \partial \phi_{i}} \\ {\vdots} \\ \end{array}\right] \approx \left[\begin{array}{c}{\partial l(\hat{\theta}) / \partial \hat{\theta}_{1}} \\ {\partial l(\hat{\theta}) / \partial \hat{\theta}_{2}} \\ {\vdots} \\ {\partial l(\hat{\theta}) / \partial \hat{\theta}_{i}} \\ {\vdots} \\ \end{array}\right]=\nabla_{\hat{\theta}} l(\hat{\theta})
那么整个MAML的过程其实就很简单了:

从 \phi^0 开始,先用一个batch的任务训练(这里任务就相当于数据了),假设只用了一个任务,即任务m。
那么先用 \phi^0 作为初始化参数,用task m的数据作为训练集,梯度下降一次,得到了 \hat{\theta}^{m} ,这是已经训练好的模型了(我们假设只梯度下降一次)。
然后我们要得到模型关于 \hat{\theta}^{m} 的梯度信息,那就再求一次梯度,但是我们就不用这个梯度对 \theta 梯度下降了,而是对 \phi 梯度下降。
不停的计算不同的task的梯度,对 \phi 进行更新,就得到了最终的 \phi 。
这就是MAML的思想。


