什么是孤子？什么是孤子解？

孤子是最先由罗素发现并记录的：

1834年秋，英国科学家、造船工程师罗素在运河河道上看到了由两匹骏马拉着的一只迅速前进的船突然停止时，被船所推动的一大团水却不停止，它积聚在船头周围激烈地扰动，然后形成一个滚园、光滑而又轮廓分明的大水包，高度约为0.3～0.5米，长约10米，以每小时约13公里的速度沿着河面向前滚动。罗素骑马沿运河跟踪这个水包时发现，它的大小、形状和速度变化很慢，直到3～4公里后，才在河道上渐渐地消失。罗素马上意识到，他所发现的这个水包决不是普通的水波。普通水波由水面的振动形成，振动沿水平面上下进行，水波的一半高于水面，另一半低于水面，并且由于能量的衰减会很快消失。他所看到的这个水包却完全在水面上，能量的衰减也非常缓慢(若水无阻力，则不会衰减并消失)。并且由于它具有圆润、光滑的波形，所以它也不是激波。
罗素将他发现的这种奇特的波包称为孤立波，并在其后半生专门从事孤立波的研究。他用大水槽模拟运河，并模拟当时情形给水以适当的推动，再现了他所发现的孤立波。罗素认为孤立波应是流体力学的一个解，并试图找到这种解，但没有成功。
十年后（1845年）罗素向英国科学促进会报告了自己的观点，但却没能说服他的同事们，罗素所发现的孤立波现象也未能引起人们的注意。50年以后即1895年，两位数学家科特维格与得佛里斯从数学上导出了有名的浅水波 \mathrm{KdV} 方程，并给出了一个类似于罗素孤立波的解析解，即孤立波解，孤立波的存在才得到普遍承认。
在罗素逝世100周年即1982年,人们在罗素发现孤立波的运河河边树起了一座罗素像纪念碑，以纪念148年前他的这一不寻常的发现。

按传统的观点，上述的水团只能是一个波包，而波包又是由一系列不同频率的平面波叠加而成的。由于介质中的波速与频率有关，所以波包中不同频率的平面波将以不同速度传播（色散），这样就使波的合成图像随时间发生变化，最后波包将完全消失。而实际上，这种不弥散的波包是非线性效应与色散效应相抵消所致。具体而言，浅水波的动力学方程由 \mathrm{KdV} 方程给出：

\( \qquad \qquad \dfrac{\partial u}{\partial t}+6u\dfrac{\partial u}{\partial x}+\dfrac{\partial^{3} u}{\partial x^{3}}=0 \)

其中 u 为振幅。

考虑行波解：令

\qquad \qquad u(x,t)=f(\zeta)=f(x-ct)

其中 c 为波速。

则方程可化为对变量 \zeta 的常微分方程：

\( \qquad \qquad \dfrac{\mathrm{d}^3f}{\mathrm{d}\zeta^{3}}+(6f-c)\dfrac{\mathrm{d}f}{\mathrm{d}\zeta}=0 \)

可以解出孤子解：

\( \quad \begin{align} u(x,t)&=f(x-ct)\\ &=c'+\dfrac{1}{2}c \cdot \mathrm{sech}^{2}\Big[\dfrac{1}{2} \sqrt{c}(x-ct+x_{0})\Big]\\ \end{align}\)

其形状类似钟形曲线。

在特定的情况下还有多孤立子解，例如对于初始条件 u(x,0)=6\mathrm{sech}^{2}x ， \mathrm{KdV} 方程有双孤子解，为：

u(x,t)=12 \dfrac{4\cosh(2x-8t)+\cosh(4x-64t)+3}{\big[3\cosh(x-28t)+\cosh(3x-36t)\big]^2}

波的图像变化如图：

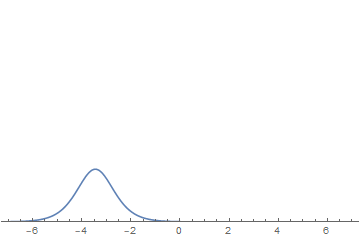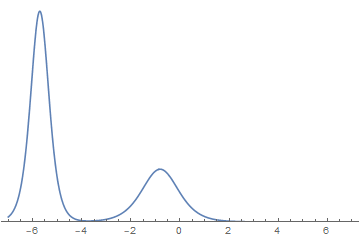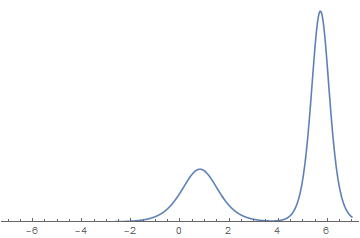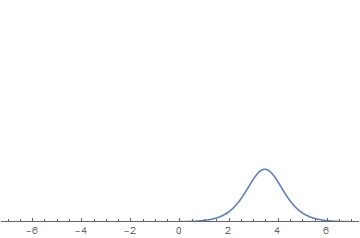
由图可见，两孤立子相遇前后波形并未改变，但发生了相移（相遇前后波各自平移了一定距离），类似于粒子的碰撞。

除了 \mathrm{KdV} 方程，还有一些偏微分方程也可以给出孤立子解，如非线性薛定谔方程、户田非线性晶格方程等。只要色散与非线性同时存在，并在一定条件下达到“平衡”，就会产生孤立子。

从物理的本质来看，孤立子是一种形态稳定的准粒子，他们由非线性场所激发，能量不会弥散。这种准粒子具有粒子的一切特性，如能量、动量、质量、电荷及自旋等；同时又具有波动的特征，在一切可以出现波动的介质里，都可以存在。除了在浅水层外，在深水层乃至固体介质、电磁场、等离子体，以及生物体和微观粒子的表现中都可以观察到孤立子现象。

看一个非常简单的物理中的孤子解，然后考察它的性质。首先写一个1+1维经典场论，它的Lagrange量密度

\mathcal{L}=\frac{1}{2}\partial_{\mu} \phi\partial^{\mu} \phi-\frac{\lambda}{4}\left(\phi^2-v^2\right)^2,\quad v=\sqrt{\frac{m^2}{\lambda}}

求出运动方程

\frac{d^{2} \phi}{d t^{2}}-\frac{d^{2} \phi}{d x^{2}}=-\lambda\left(\phi^{2}-v^{2}\right) \phi

讨论它的静态解，也就是令 d\phi/dt=0 。显然当势能取最小值，即 \phi(x)=\pm v ，我们有两个独立的基态解。若取边界条件 \phi(\infty)=v ,\ \phi(-\infty)=-v ，会有一个孤子解

\phi(x)=v \tanh \left[\frac{m}{\sqrt{2}}\left(x-x_{0}\right)\right]

这称为kink，其中 x_0 是积分常数，可以看作孤子的位置， x_0=0 时的图像如图1。当然取相反的边界条件也可以得到孤子解 \varphi(x)=-\phi(x) ，称为antikink。

能量密度为

\begin{aligned} \epsilon&=\frac{\partial \mathcal{L}}{\partial(\partial_0 \phi)}\partial_0\phi-\mathcal{L}\\&=\frac{1}{2}\left(\frac{d \phi}{d t}\right)^{2}+\frac{1}{2}\left(\frac{d \phi}{d x}\right)^{2}+\frac{\lambda}{4}\left(\phi^{2}-v^{2}\right)^{2}\\&=\frac{m^4}{2\lambda} \text{sech}^4\left[\frac{m}{\sqrt{2}}(x-x_0)\right] \end{aligned}

图像如图2。

能量的局域性暗示孤子可以被看作一种粒子。接下来积分求出总能量

E=\int_{-\infty}^{+\infty}\epsilon dx=\frac{2 \sqrt{2}}{3} \frac{m^{3}}{\lambda}

我们对这个解作Lorentz变换：

\phi(x, t)=v \tanh \left[\frac{m}{\sqrt{2}} \frac{\left(x-u t-x_{0}\right)}{\sqrt{1-u^{2}}}\right]

这时重新算一下总能量，发现任意时刻都有

E'=\frac{E}{\sqrt{1-u^2}}

那么这个解就可以被看作是具有能量 E ，以速度 u 运动的粒子。很重要的是，随着时间推移，场和它的能量密度的构型仅仅发生了中心的平移，并没有发生耗散，kink确实就像是粒子。它像是不受任何阻碍地在运动，因而称为孤子。

此外，这个粒子还具有某种守恒的拓扑荷，因而又称为拓扑孤子。要看到这一点，首先定义拓扑流

J_{\mathrm{top}}^{\mu}=\frac{1}{2 v} \epsilon^{\mu \nu} \partial_{\nu} \phi

对应的拓扑荷为

Q_{\mathrm{top}}=\int_{-\infty}^{\infty} d x J^{0}=\frac{1}{2 v} \int_{-\infty}^{\infty} d x \partial_{1} \phi=\frac{1}{2 v}[\phi(\infty)-\phi(-\infty)]

于是kink带有+1的拓扑荷，而antikink带有-1的拓扑荷。有限能量的过程不可能改变场在无穷远处的渐近行为，因此这个拓扑荷是守恒的。这个守恒荷来自基态空间和场构型的非平凡拓扑结构，而不是根据Noether定理来自某种连续对称性，因而称为拓扑荷。

凝聚态和高能场论中的kink，vortice，monopole，domain wall，skyrmion，instanton，宇宙学中的cosmic string，都是孤子。

更新：多说一些拓扑荷的事情。

就像用规范场的Noether荷区分不同类型的基本粒子，我们也考虑一些守恒量，以区分不同类型的场的孤子解。既然我们是考虑一个能看作粒子的场构型，那么能量的局域性要求能量密度在无穷远处趋于零。因为有限能量的过程无法改变场在无穷远处的行为，所以我们只需要场在无穷远处行为的拓扑分类。

我们将场 \phi 看作是 \mathbb{R}^d 到它取值构成的流形 Y 的映射，孤子解的渐近行为 \phi^\infty 就是 \mathbb{R}^d上无穷远处的球面 S_{\infty}^{d-1} 到场处于基态时的取值构成的子流形 \mathcal{V} \subset Y 的映射。我们用 \phi^\infty 的同伦类，也就是同伦群 \pi_{d-1}(\mathcal{V}) 的元素，区分不同类型的孤子解。

回到这里 d=1 的情形， S_{\infty}^{d-1}=\left\{ +\infty,-\infty\right\} ， \mathcal{V}=\left\{ v,-v \right\} ， \pi_{0}(\mathcal{V}) 也就是拓扑上不等价的基态集合，场构型也就是 \pi_{0}(\mathcal{V}) \times \pi_{0}(\mathcal{V}) 的元素。这里 \mathcal{V} 包含两点，就应该有4种拓扑上不等价的构型。假设场由 \left(v_{1}, v_{2}\right) \in \pi_{0}(\mathcal{V}) \times \pi_{0}(\mathcal{V}) 描述，如果 v_1=v_2 ，它表示一个全局的基态 \phi(x)=\pm v ；如果 v_1 \neq v_2 ，它表示非平凡的孤子解 \phi(+\infty)\neq \phi(-\infty) ，根据 \phi(\pm \infty) 的具体取值，可以是kink或antikink。这里定义的拓扑荷就是反映 \phi^\infty 同伦类的一个拓扑不变量。

对 d=2 的情形，我们用 \pi_1(\mathcal{V}) ，也就是 \mathcal{V} 的基本群，来分类场构型。它的非平凡元素有vortex的特点，例如图3二维XY模型中的自旋构型，相应的拓扑不变量就称为缠绕数。

规范场论中常常用Chern数来分类孤子。它们是Chern形式在全空间上的积分，Chern形式是由势 A 和场强 F 构造的规范不变的偶数次微分形式，局部上可由Chern-Simons形式的外微分给出，更多内容可以参看 @Again 的回答

以及 @史诗生物 的专栏

References:

E. J. Weinberg, Classical Solutions in Quantum Field Theory: Solitons and Instantons in High Energy Physics, Cambridge, 2012.

N. Manton & P. Sutcliffe, Topological Solitons, Cambridge, 2004.