海明距离详细解释？

海明码能够纠正一位比特的错误。一个长度为$m$的数据中增

加$k$位冗余位，构成一个 n=m+k 位的码字，然后用 k 个监督关系式产生的 k 个校正因子来检测和纠正错误。为了能够纠正一个比特的错误，数据长度和冗余位的数目必需满足公式\ref{eq:hamming1}，海明码的编码效率效为： R=m/(m+k) 。

2^k \geq m+k+1 (1)

公式(1)中， m 是数据的长度， k 是海明码校验位的个数。

海明码利用监督公式对数据进行交叉校验，利用监督公式的特性可以直接定位出错数据的位置。因为二进制数据中数据的取值只有两种状态0和1，因此只要知道出错的位置，修改就变得非常的容易，只要对出错位置的数据取反就可以达到纠正的目的。例如接收端收了一串二进制数据101011，经过海明码计算后得到的数字是3，说明数据中的第3位的数据出现了错误，纠正时只需要把第三位的1取反变成0即可，纠正后的二进制串是100011。

公式(1)中海明码虽然可以实现数据的纠错，但是只能实现一个比特数据的纠错。如果数据中有多个比特同时出现错误，就必须使用更加复杂的海明公式。海明码的纠错能力和最小码距有关。

码距是编码系统中两个编码之间不同的二进制的位数，例如数据1010和数据1111的码距就是2，因为它们的第2和第3位数据不同，数据不同的位数是2，因此码距是2。最小码距（用 D 表示）是编码系统中码距的最小值。码距和纠错的能力如下：

1. 如果要检测 e 个错误，最小码距应该满足： D>=e+1
2. 如果要纠正 t 个错误，最小码距应满足： D>=2t+1
3. 如果要检测 e 个错误同时纠正 t 个错误，最小码距应该满足： D>=e+t+1 , (e>=t)

本节主要讨论检测一位错误且纠正一位错误的情况，因此最小码距码距$D>=3$，需添加的冗余位的数目需满足公式(1)

校验位计算示例

已知原始数据为1001011,采用Hamming Code编码后，求实际发送的数据？

求解过程如下：

1. 计算需要的校验位数目。从题目中可知数据为的长度为7，即 m=7 ，带入公式 m+k+1\le2^k
2. 后得到 k<=4 ，为了减少冗余$k$取最小值4。最后实际发送的数据长度为 7+4=11 位。
3. 重新排列数据。定义4个校验位分别是 a1, a2, a3, a4 。根据海明码原则组合排列7为数据和4位校验码。校验码的位置分别是 1=2^0, 2=2^1, 4= 2^2, 8=2^3 。排列后的顺序如表1.4所示。

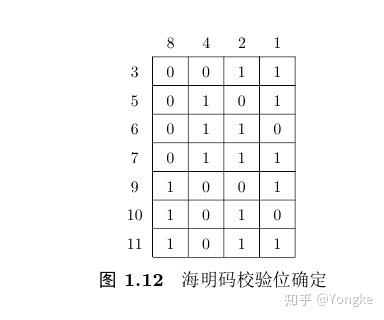
4. 计算每个校验位的值。根据图1.12所示，位置1（ 2^0 )，2（ 2^1 ），4（ 2^2 ），8（ 2^3 ）存放校验数据。在图1.12中的最后一列，列名称是1，数字3，5，7，9，11的二进制数在该列的数据为1，因此位置1对这些位置进行监督，同理，列名为2，4，8的位置对二进制数在该列为1的位置进行校验。公式1.7是海明码计算的具体公式，公式中的 X_3 为表1.4中序号/下标为3的数据， X_5 为表1.4中序号/下标为5的数据，其它以此类推。符号 \oplus 表示异或运算。把表1.4中的数据带入公式(1.7)中可以得到：

\begin{split} a1&=X_3\oplus X_5\oplus X_7\oplus X_9\oplus X_{11} =1\oplus0\oplus1\oplus0\oplus1=1\\ a2&=X_3\oplus X_6\oplus X_7\oplus X_{10}\oplus X_{11} =1\oplus0\oplus1\oplus1\oplus1=0\\ a3&=X_5\oplus X_6\oplus X_7 =0\oplus0\oplus1=1\\ a4&= X_9\oplus X_{10}\oplus X_{11} =0\oplus1\oplus1=0 \end{split} (1.7)

5. 带入校验数据得到发送数据。把 a1,a2,a3,a4 分别带入表1.4中，得到一个新的数据序列 10110010011，这个新序列就是发送端发送出去的数据，也是线路上传输的数据。如果数据没有发生冲突，这也将是接收方收到的数据。

海明码纠错

如果接收端收到的数据10110110011,接收方需要先计算校验位 a1,a2,a3,a4 的值，计算的值再和数据中的校验位进行异或比较,公式（1.8）为接收端的计算公式：

\begin{split} h_1&=X_3\oplus X_5\oplus X_7\oplus X_9\oplus X_{11} \oplus a1\\ h_2&= X_6\oplus X_7\oplus X_{10}\oplus X_{11}\oplus a2\\ h_3&= X_5\oplus X_6\oplus X_7\oplus a3\\ h_4&=X_9\oplus X_{10}\oplus X_{11}\oplus a4 \end{split} （1.8）

公式（1.8）中的监督公式都分为两个部分，前面的使用 X_i 表示的部分是和发送端一模一样的计算公式，后面的 ai 是发送端计算不需要的，是数据中的校验位。这个计算的本意是接收端重新计算一次校验码，然后和数据中校验码进行比较。如果自己计算的校验码和数据中的校验码相同，记为0，不同则记为1。

因为在新的数据串中a1和$X_1$是同一个数据位，a2和 X_2 是同一个数据位，a3和 X_4 是同一个数据位，a4和 X_8 是同一个数据位.因此公式（1.8）也可以表示为（1.9）.

\begin{split} h_1&=X_3\oplus X_5\oplus X_7\oplus X_9\oplus X_{11} \oplus X_1\\ h_2&=X_3\oplus X_6\oplus X_7\oplus X_10\oplus X_{11}\oplus X_2\\ h_3&=X_5\oplus X_6\oplus X_7\oplus X_4\\ h_4&=X_9\oplus X_{10}\oplus X_{11}\oplus X_8 \end{split} （1.9）

计算结果按照 h_4h_3 h_2 h_1 的顺序进行排列，如果结果等于0说明数据没有出错；如果结果不等于0，说明数据出错。把该数据转 化为10进制数，就是出错数据的位置。因为二进制数中每一位置只有2种状态，0或者1。因此知道错误的位置后，改正错误就非常简单，把对应的数据取反即可。

把接收到的数据 10110110011 代入公式（1.8）中得到：

\begin{split} h_1&=1\oplus0\oplus1\oplus0\oplus1\oplus1=0\\ h_2&=1\oplus0\oplus1\oplus1\oplus1\oplus0=1\\ h_3&=0\oplus1\oplus1\oplus1=1\\ h_4&=0\oplus1\oplus1\oplus0=0 \end{split}

新的数据 h_4h_3h_2h_1=0110 ，转换为十进制数值为6，因此说明接收到的数据中第6位出错，将第六位数据取反就可以得到正确的原始数据，原始数据为 10110010011 。

在这个例子中，数据的第6位出错，接收方在收到数据后按照规则对数据进行重新计算时，发现第2位和第4位存放的校验结果不正确，将这两个校验位的序号相加 2+4=6 ，正好就是发生错位的位置。