如何理解「对数」？

宫崎骏的电影《起风了》，里面的主角是一个飞机设计师，绘制图纸的时候总是手里拿了一个长条状的东西：

这是什么东西？拿来干什么用的？还得从对数说起。

1 在数轴上表示对数

1.1 数轴和加法

数轴上的数和后继的数之间是 +1 的关系， 1=0+1 ， 2=1+1 。我们把它称为 +1坐标系吧。

把 +1 的关系变成 +2 ，数轴上的就全是偶数了。数轴还是那根数轴，可是坐标系变了，我们把它称为 +2 坐标系吧。

+2 坐标系中，上面的蓝色的字表示真实的数值，下面的灰色的数字表示顺序，也就是说序号为0的数值是0，序号为1的数值是2，序号为2的数值是4。 +1 坐标系也有序号和数值，只是刚好都相等。

从 +1 坐标系到 +2 坐标系有什么变化？只是简单的放大了一下数轴的尺度。

1.2 数轴和乘法

我们试试把加法数轴变为乘法数轴（这点是没有什么问题的，加法和乘法等价的，即乘法完全可以被加法替代），当然要从1开始计算，因为从0开始的话，乘法的结果永远是0。

这种数轴我把它称为 \times 2 坐标系。

1.3 数轴和对数

\times 2 坐标系其实和对数有关，我们看下：

灰色的数字就是对数了，稍微修改下看得更清楚：

按照现在的术语， \times 2 坐标系其实就是指数坐标系。但是，在刚出现的时候，其实 \times 2 坐标系和 +2 坐标系没啥区别，所以当时的人也没有区别对待，更没有给出指数这个名字。

数学家其实是很吝啬的，没有那么容易就给出命名，必须得有充分的理由。可以参看下 虚数是否真实存在 中的一些思考。

说回来，8的对数就是距离1有几个格子，这里是3个格子，可以推出8的对数是3。所以有种简单的计算8的对数方法， ((8/2)/2)/2=1 ，除了3次，对数就是3。

lg\sqrt{2}=0.5 ，所以 4\sqrt{2}=2^{2.5} ：

也可以这么计算，有 (4\sqrt{2}/2)/2=\sqrt{2} ，除不尽有个余项，而 lg\sqrt{2}=0.5 ，所以可以求出 4\sqrt{2}=2^{2.5} 。呃，似乎运算已经比较复杂了，不如用计算器了。

求两个数之间的关系也比较简单，比如8和4，4距离1两个格子，8距离1三个格子，所以8^\frac {2}{3}=4 。

2 对数数轴与天文数字

2.1 对数数轴

我们要是想把为 \times 2 坐标系继续画下去是困难的，因为指数增长太快了：

尽量缩小才画到对数为5的地方，我相信你已经快看不清了，如果画到对数为100的地方，地球都摆不下这个长度。

我们可以保持对数值等距离摆放，这就是对数坐标系：

是不是可以摆下更多的对数了？

2.2 天文数字

对数是将数轴进行强力的缩放，再大的数字都经不起对数缩放，如果我选用10为底的话，一亿这么大的数字，在对数数轴上也不过是8。这对于天文学里的天文数字简直是强有力的武器。

要是不进行缩放的话，地球和太阳是不可能同框的：

此处有可以操作的内容，需要流量较大，请斟酌打开。
点击此处前往操作。

3 对数尺

3.1 乘除法

我们把对数坐标系中剩余的数字补齐：

其实绕了这么一大圈，就是把对数值给摆在了数轴上，不过历史可能就是这么曲折，要知道历史发展到这一步都还没有给对数一个名分。什么时候给的名分我们后面再说。

因为 log_2 符号太累赘了，所以我们把它去掉，心中知道是 log_2 就好了：

我们把这个刻在一把木尺上就得到了一把对数尺：

对数尺有什么用？我们可以很简单的来计算乘法，下面是计算 2\times 3=6 (记住，对数尺的起点是1，不是0)：

log 有一个很重要的特性， log(xy)=log(x)+log(y) ，所以对数尺可以用加法的方式来计算乘法(在这里以什么为底不重要，只要是同底就可以）。而 log\frac{x}{y}=logx-logy ，所以可以通过减法计算除法。

如果对数尺上的坐标可以标细一点，就可以计算类似 2.15\times 3.782 这样比较复杂的乘法。

3.2 幂与开方

对数尺还可以进行幂运算和开方运算，下面计算 \sqrt9=3 ：

logx^{\frac{1}{2}}=\frac{1}{2}log(x) ，所以对数的 \frac{1}{2} 处就是对数的平方根，以此类推可以计算 n 次方根。注意对数尺的起点是1哦，不是0。

计算 \sqrt[3]9 也一样轻松(这里尺子的刻度不太细，不过估读出来是2.0x):

3.3 亲自动手

我们自己来把玩下对数尺吧：

此处有可以操作的内容，需要流量较大，请斟酌打开。
点击此处前往操作。

3.4 对数和对数尺的重要性

16世纪，苏格兰人纳皮尔，用类似上面文章描述的思路（细节很不一样，不过方向是相同的），发明了对数这个词，他把对数称为人造数。而当时还没有完整的指数概念，直到17世纪末人们才认识到对数是指数的逆运算。

对数发明之后，在当时的科学界造成了很大的影响，专门有人长途跋涉跑来见纳皮尔，就为了表达感谢。天文学家欣喜若狂：“对数让计算时间缩短从而延长天文学家的寿命”。伽利略也说过：“给我时间，空间和对数，我可以创造出一个宇宙”。

刚开始对数的运算是通过查对数表来完成，后来，更方便的对数尺也出现了，这就是最早的计算尺。

3.5 计算尺

最早的计算尺就是对数尺，随着时间的推移，对数尺增加了很多别的数学工具，演化成了威力更大的计算尺。上面除了有对数、还有三角函数、倒数等等数学工具，可以查看 计算尺，或者 三百年辉煌，计算尺传奇 了解更详细的信息。

文章开头《起风了》的主角手里拿的就是计算尺：

在计算器发明之前，炮兵打个炮啊、工程师修个桥啊、设计师造个飞机啊，都离不开计算尺。

没有计算尺之前，人类社会是匍匐前进，有了计算尺之后，是走步前进。而计算器、计算机出现之后，真正是跑步前进。

历史的车轮总是向前，计算尺的历史使命已经完成，这篇小文只是尝试让大家短暂的回到过去，体验一下对数、对数尺、计算尺的重要性。

4 结论

对数是作为一个数学工具出现，主要解决两方面的问题：

• 处理天文数字。
• 简化乘、除、开方、乘方运算。

这两个作用，让对数这个数学工具与 +1 , +2 产生了本质区别，也有了拥有“对数”这个名字的资格。

参考文章： 观《起风了》 探究计算尺 。

跟着马同学，看图学数学，欢迎加入马同学图解数学

数学的基本运算可分为三个等级。第一级为加、减运算，虽然加减法的概念在公元前20世纪的古埃及数学家艾哈迈斯(Ahmes)的纸草书中就有体现，但今天的加号“+”和减号“-”，最早有史料记载的，是在15世纪末的德国人的手稿中，现保存于德国德累斯顿(Dresden)图书馆^[1]。

后来，人们发现在遇到“连加”或“连减”时，加减法的效率很低，于是就发明了第二级运算——乘法和除法以及与此对应的乘号和除号。在西方，“×”被称为“圣安德鲁斜十字(St. Andrew’s Cross)”。安德鲁是耶稣的12门徒之一，由于其被钉死在斜十字架上，因此，斜十字架也成为圣安德鲁斜十字。现代意义上的“×”号最先出自于1631年英国数学家奥特雷德(William Oughtred)的《数学之钥》中。

1698年，莱布尼兹(Gottfried Wilhelm Leibniz)^[2]在其给瑞士数学家雅各比·伯努利(Jacob Bernoulli)的信件中首次使用“·”表示乘法，以此来避免乘号“×”和字母“X”的混淆。不过，后来在向量代数中，用“·”表示“数量积”或“内积”，而“×”则表示“向量积”或“外积”，这就算是另一种区分方法了。

今天用的除号“÷”称为“雷恩记号”。它是瑞士数学家雷恩(Rahn)在其1659年出版的一本代数书中首先使用，在1688年，这本书被译成英文，这个符号也随之通用起来。

但人们还不满足，因为人们遇到了“连乘”和“连除”，即“乘方”。而且，乘方有两种逆运算，分别是“开方”和“对数”。这是第三级运算与加减乘除的不同之处。

法国数学家笛卡尔(Descartes)在1637年定义了现代乘方符号，即在字母或数字的右上角用小的阿拉伯数字表示指数。1732年卢贝(Loubere)首次使用根号来表示开方，并逐渐流行起来。

“开方”的诞生似乎顺理成章，但是乘方的另一种逆运算——“对数”，就有些“难产”了。

斯蒂菲尔(Michael Stifel)^[3]是德国德国哥尼斯堡大学的数学讲师，1544年，他写了一本书叫《整数的算术》，在这本书中他应用“一一对应”的方法几乎造就了一座数学丰碑。

斯蒂菲尔在书中写道：“关于整数的这些奇妙性质，可以写成整本整本的书！”下面就是他书中列出的两列数字：

可以看出，上一列其实就是通项公式为 2^n 的等比数列（ n 为整数），他称其为“原数”；下一列则是一个由整数构成的等差数列，他称其为“代表数”，德语是Exponent，也可译为“代言人”。

他发现，两个“原数”相乘等于“代表数”相加后得到的“代表数”所对应的“原数”；“原数”相除等于“代表数”相减后得到的“代表数”所对应的“原数”。即，利用这两列数可以把较为复杂的乘除法变成较为简单的加减法。

其实，在我们看来，这个结论没有什么神奇之处，因为所谓的“代表数”其实就是“原数”以2为底的对数。但是在当时，这种计算方法思想是开创性的。

不过遗憾的是，在斯蒂菲尔的那个年代还没有分数指数的概念，因此在处理指数不是整数时遇到了巨大的阻力，最后，他放弃了对这种计算方法的进一步研究，而只是停留在了整数上。不过，斯蒂菲尔也并非全然无功，他的前驱性工作，成为纳皮尔发明对数的“巨人肩膀”。

约翰·纳皮尔(John Napier)^[4]是苏格兰数学家、物理学家兼天文学家。1614年，其在爱丁堡出版了《奇妙的对数定律说明书》中提出了对数的概念。

"看起来在数学实践中，最麻烦的莫过于大数字的乘法、除法、开平方和开立方，计算起来特别费事又伤脑筋，于是我开始构思有什么巧妙好用的方法可以解决这些问题。"

--约翰·纳皮尔，《奇妙的对数定律说明书》^[5]

作为数学家、物理学家兼天文学家，他在计算各种行星轨道数据时，也被浩瀚的计算量所折磨，因此很痛恨这些乏味的重复性工作。为了解决这一问题，他用了20年的时间，进行了数百万次的计算，发明了对数和对数表，听起来很矛盾，一个不想做重复工作的人结果做了20年重复性工作。但是，他的努力确实为后人减少了大量的重复性工作，大大减少了数学家、天文学家的计算量，由此可见，这在天文学界算得上是一项伟大的发明了，看看名人们对其的评价就能看出其重要性^[6]。

“对数的发明、解析几何的创始和微积分的建立是17世纪数学的三大成就。”

——恩格斯

“对数的发现，因其节省劳力而延长了天文学家的寿命。”

——拉普拉斯

“给我空间、时间及对数，我就可以创造一个宇宙。”

——伽利略

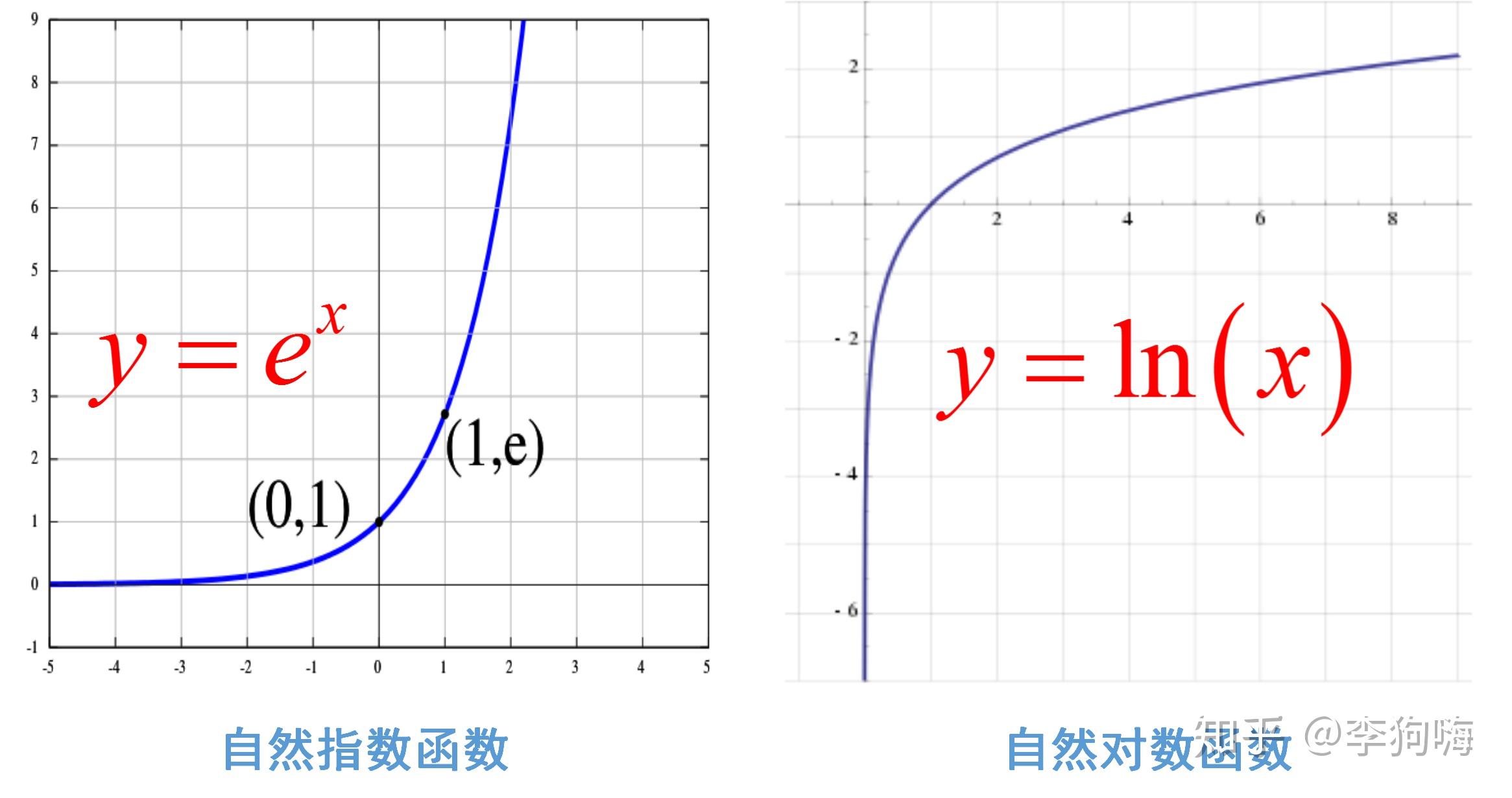
对数使得手算变得简单而且快多了，也因此为后来许多科学进步开启了大门。那么如何理解对数？一个直观的解释是：对数指的是到达某一数量所需要的时间。这里先介绍自然对数。即以 e 为底的对数。

例如，有一个土豪投资的项目正好满足年利率为100%的连续复利。但是这个土豪小学文化，数学水平也就加减乘除，假设你是这个项目的负责人，想劝说土豪再多投资，如果跟他说什么连续复利、什么100%、什么指数增长，土豪听不懂啊，你再这么说下去感觉在欺负人啊！土豪就发话了：“别整那些没用的，你就告诉我，我的钱啥时候能涨到10倍，100倍，1000倍？”你有些发懵了，一般人不怎么问啊，不都是问一年后是多少，两年后是多少之类的吗？所以这里的问题就是知道时间求数量的逆向问题——知道数量求时间。土豪就是土豪，有的是钱，他只想从翻倍时间的长短来判断哪项投资赚得快。因此，这里就要用到对数，在这样一个年利率为100%的连续复利增长模型下，如果你想得涨到你本金10倍，你需要等待的时间其实就是 ln(10)≈2.302 年，到100倍所需时间就是 ln(100)≈4.605 年，到1000倍所需时间就是 ln(1000)≈6.907 年。

e^x 与 ln(x)

e 和 ln 好像是孪生一对， e^x 表示单位数量经过x个单位时间增长后的数量（在单位时间增长率为100%的连续复利情况下）。那么在单位时间增长率为50%的连续复利情况下，增长4年和单位时间增长率为100%的连续复利情况下增长2年是一样的。因为 e^x=e^{rate·time}=e^{1·time}=e^{time} 。所以，可以看出，不管利率是多少，通用的连续复利模型 e^{rate·time} 都可以描述。

ln(x) 表示单位数量增长到 x 个单位数量所需要的时间（在单位时间增长率为100%的连续复利情况下）。 ln(x) 正好与 e 相反， e^x 表示输入时间得到数量， ln(x) 表示输入数量计算达到这么多数量所需时间。

自然对数的计算

有人可能会觉得对数这种算法很奇怪，不知道为什么它能够将乘法转变为加法，把除法转化为减法，但如果掌握其“数学内涵”的话，就好理解了。

先看 ln(1) ，它是多少呢？我们都知道答案是0，因为其数学内涵是：单位数量增长到单位数量的1倍时所需要的时间，因为现在就已经是现在数量的1倍了，所以无需再给予时间让它增长了。

那么，如果是分数呢？例如，得到现在数量的1/2需要多久。我们知道ln(2)表示在单位时间增长率为100%的连续复利情况下翻倍所需要的时间。那我们取反，就得到了退回现在的一半所需要的时间（如果是等待所花费的时间为正，如果是“时光倒流”的话，时间则为负，是不是很直观？！）。因此 ln(0.5)=ln(2)^{-1}=-ln(2)=-0.693

那么能不能对负数取对数呢？答案是否定的，因为一个给定的数量不能增长为一个负数也无法退回成为一个负数，再怎么等待下去或者再怎么“时光倒流”，这种情况也不可能发生，所以没有定义。

为了增长到30倍，我们可以等ln(30)个单位时间，也可以先等增长3倍所需要的时间ln(3)再等个增长10倍所需要的时间ln(10)，效果是一样的。因为在增长率不变的连续复利情况下，给定一个初始值，那么增长到初始值的x倍所需要的时间是一定的，与初始值的大小并没有任何关系。即 ln(a*b)=ln(a)+ln(b) 。

那么 ln(5/3) 呢，意味着计算增长到现在的5倍所需时间减去以5倍为基数退回到其1/3所需时间。所以有 ln(a/b)=ln(a)-ln(b) 。

相乘增长量=时间相加

相除增长量=时间相减

但是对于增长率不是100% 的连续复利模型呢？

其实同样适用。

例如 ln(30)≈3.4 可以看为是在单位时间利率100%连续复利情况下变为原来的30倍所需要的时间为3.4个单位时间。

由于 e^x = e^{rate·years} 即 e^{100\%·3.4}=30

当我们计算单位时间利率为5%，增长到30倍所需时间时。其实只要保证 rate·time=3.4 即可。即 0.05·time=3.4 ，所以 time=68

72法则

这是一种快捷算法，因为实际中银行的利率不可能是100% ，但是我们经常想知道本金到底什么时候能够翻倍。而对于利率为100% 的连续复利，如果要翻倍就需要ln(2)=0.693个单位时间。

那么对于小利率呢，为了方便计算现将利率乘以100，但注意是百分数。那么0.693也要乘以100，等于69.3。

由 rate·time= ln(2) ，可知 time= 69.3/rate

但是69.3并不太好分，所以我们取一个相近的，72，因为其可以被2、3、4、6、8整除。因此，翻倍所需时间大约是 72/rate ，这就是“72”法则。当然，如果想计算增长到3倍的话那就是“110”法则了。

参考

1. ^陈仁政,不可思议的e [M], 北京,科学出版社
2. ^Gottfried Wilhelm Leibniz.  https://en.wikipedia.org/wiki/Gottfried_Wilhelm_Leibniz
3. ^Michael Stifel.  https://en.wikipedia.org/wiki/Michael_Stifel
4. ^John Napier.  https://en.wikipedia.org/wiki/John_Napier
5. ^Napier's bones.  https://en.wikipedia.org/wiki/Napier%27s_bones
6. ^Demystifying the Natural Logarithm (ln).  https://betterexplained.com/articles/demystifying-the-natural-logarithm-ln/