Goldener Schnitt

Goldener Schnitt

Der Goldene Schnitt (lateinisch sectio aurea „Goldener Schnitt“, proportio divina „göttliche Proportion“), gelegentlich auch stetige Teilung einer Strecke, ist ihre Zerlegung in zwei Teilstrecken in der Weise, dass sich die längere Teilstrecke zur kürzeren Teilstrecke verhält wie die Gesamtstrecke zur längeren Teilstrecke. Das Konzept ist bereits seit der Antike zur Zeit des Euklid bekannt. Der Goldene Schnitt findet häufige Anwendung in der Kunst, taucht aber auch in der Natur auf.

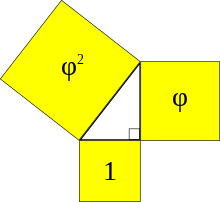
In mathematischen Formeln ausgedrückt, gilt für den Goldenen Schnitt zweier Teilstrecken $a$ und $b$ (siehe Bild):

${\frac {a}{b}}={\frac {a+b}{a}}\quad$ oder $\quad {\frac {a}{a+b}}={\frac {b}{a}}$.

Das mittels Division dieser Größen als Zahl berechnete Teilungsverhältnis des Goldenen Schnittes ist eine dimensionslose, irrationale Zahl, das heißt eine Zahl, die sich nicht als Bruch ganzer Zahlen darstellen lässt. Die Folge ihrer Nachkommastellen zeigt daher auch kein periodisches Muster. Diese Zahl wird ebenfalls als Goldener Schnitt bezeichnet. Als mathematisches Symbol für den Goldenen Schnitt wird meist der griechische Buchstabe Phi ($\Phi$, $\phi$ oder $\varphi$, heutige Aussprache [fi:]), seltener auch Tau ($\mathrm {T}$, $\tau$) oder $g$ verwendet. Es gilt

$\Phi ={\frac {a}{b}}={\frac {a+b}{a}}={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}6180339887$, wobei ${\sqrt {5}}$ die Quadratwurzel aus 5 bezeichnet. Seit 2021 sind 10 Billionen Dezimalstellen des Goldenen Schnittes bekannt.

Aus Sicht der Mathematik besitzt der Goldene Schnitt zahlreiche besondere Eigenschaften. Neben der geometrischen Auffassung kann er auch als die positive Lösung der quadratischen Gleichung $x^{2}-x-1=0$ definiert werden. Er ist damit eine algebraische Zahl vom Grade 2. Bemerkenswert ist seine enge Verbindung zu der Fibonacci-Folge, die sich durch die explizite Binet-Formel ausdrückt, obgleich die Fibonacci-Folge zunächst nur rekursiv, also implizit erklärt ist. Darüber hinaus konnte gezeigt werden, dass der Goldene Schnitt unter den irrationalen Zahlen (bis auf eine gewisse Form der Äquivalenz) am schlechtesten durch Brüche angenähert werden kann. Zentrales Argument für diese Tatsache ist seine Kettenbruchentwicklung, die nur aus der Zahl 1 besteht, ergo unter allen Kettenbrüchen am langsamsten konvergiert.

Der Goldene Schnitt ist in der mathematischen Literatur seit der Zeit der griechischen Antike (Euklid von Alexandria) nachgewiesen, war jedoch vor mehr als 2300 Jahren nur Wenigen bekannt. Vereinzelt schon im Spätmittelalter und besonders dann in der Renaissance, etwa durch Luca Pacioli und Johannes Kepler, wurde er auch in philosophische und theologische Zusammenhänge gestellt. Der Überlieferung nach erhielt er mit diesem Namen erst ab der ersten Hälfte des 19. Jahrhunderts größeren Bekanntheitsgrad. Die heute gebräuchliche Bezeichnung $\Phi$ bzw. $\varphi$ für den Zahlenwert geht auf den amerikanischen Mathematiker Mark Barr zurück, der sie um das Jahr 1909 herum einführte. Einigen bedeutenden Künstlern, wie Leonardo da Vinci, Friedrich Hölderlin oder Béla Bartók, wurde nachgesagt, den Goldenen Schnitt gezielt bei manchen ihrer Werke eingesetzt zu haben, jedoch gelten solche Aussagen als umstritten. Der Goldene Schnitt ist nicht nur in Mathematik, Kunst oder Architektur von Bedeutung, sondern findet sich auch in der Natur, beispielsweise bei der Anordnung von Blättern und in Blütenständen mancher Pflanzen wieder.

Definition

Man sagt, dass zwei Größen $a>b>0$ im Verhältnis des Goldenen Schnittes stehen, falls

${\frac {a}{b}}={\frac {a+b}{a}}$

erfüllt ist. Die Zahl

${\frac {a}{b}}=\Phi$

wird dann ebenfalls Goldener Schnitt genannt. Es muss sich bei den Werten $a$ und $b$ dabei nicht um (dimensionslose) reelle Zahlen handeln; auch eine Assoziation zu physikalischen Größen unter Zuweisung entsprechender Maßeinheiten ist möglich. Klassisch ist dabei die Veranschaulichung über das Teilungsverhältnis zweier Strecken (bei dem die längere Strecke als „Major“ und die kürzere als „Minor“ bezeichnet wird), aber auch andere Einheiten können betrachtet werden, siehe zum Beispiel Goldenes Rechteck.

In der Literatur wird der Ausdruck „Goldener Schnitt“ jedoch auch für andere Dinge verwendet. Er bezeichnet

• den Vorgang der Teilung an sich,
• gelegentlich den Teilungspunkt,
• meist jedoch die Zahl $\Phi$ selbst.

Bestimmung des Verhältnisses

Es bezeichnen $a>b>0$ die Teilstreckenlängen der Gesamtstrecke $a+b$. Es gilt dann nach Definition des Goldenen Schnitts die Relation

${\frac {a}{b}}={\frac {a+b}{a}}$.

Multipliziere mit $a\cdot b$:

$\qquad \quad a^{2}=b\cdot a+b^{2}$

$\iff \,a^{2}-b\cdot a-b^{2}=0$

a) Lösung der quadratischen Gleichung mittels Lösungsformel:

$a={\frac {b}{2}}\pm {\frac {b\cdot {\sqrt {5}}}{2}}$.

Nur die positive Lösung ist hier von Bedeutung:

$a={\frac {b}{2}}+{\frac {b\cdot {\sqrt {5}}}{2}}=b\cdot {\frac {1+{\sqrt {5}}}{2}}$.

Damit ist

${\frac {a}{b}}={\frac {1+{\sqrt {5}}}{2}}=\Phi$.

b) Graphische Lösung der quadratischen Gleichung

$a^{2}-b\cdot a-b^{2}=0$.

Setzt man $b=1$, ergibt sich die quadratische Gleichung

$a^{2}-a-1=0$,

mit $p=1$ und $q=-1$.

Deren Lösung gelingt beispielsweise mit der im Folgenden beschriebenen Konstruktion in einem kartesischen Koordinatensystem.

Nach dem Ziehen des Kreises $k$ mit Radius gleich $1$ um den Mittelpunkt $M(0|1)$ und dem anschließenden Festlegen der zueinander parallelen Tangenten an den Punkten $A(0|2)$ und $B(0|0)$, werden auf den entsprechenden Tangenten, wegen $|{\overline {AC}}|={\frac {4}{p}}$ und $|{\overline {BD}}|={\frac {q}{p}}$, die Punkte $C(4|2)$ und $D(-1|0)$ bestimmt. Eine Verbindung des Punktes $C$ mit $D$ erzeugt auf dem Kreisbogen $k$ die Schnittpunkte $E$ und $F$. Die beiden abschließenden geraden Linien ab Punkt $A$ durch $E$ und $F$ liefern auf der $x$-Achse die Punkte $X_{1}$ und $X_{2}$ mit den Längen $|{\overline {BX_{1}}}|=-x_{1}$ und $|{\overline {BX_{2}}}|=x_{2}$.

Der hier relevante positive Wert der Lösung: $|{\overline {BX_{2}}}|=x_{2}=\Phi =1{,}618033\ldots$.

Geschichte

Antike

Die erste erhalten gebliebene genaue Beschreibung des Goldenen Schnittes findet sich im zweiten Buch der Elemente des Euklid (um 300 v. Chr., siehe Innere Teilung nach Euklid), der darauf über seine Untersuchungen an den platonischen Körpern und dem Fünfeck beziehungsweise dem Pentagramm stieß. Seine Bezeichnung für dieses Teilungsverhältnis wurde später ins Lateinische als „proportio habens medium et duo extrema“ übersetzt, was als „Teilung im inneren und äußeren Verhältnis“ bezeichnet wird.

Mittelalter

Liber abbaci, MS Biblioteca Nazionale di Firenze, Codice Magliabechiano cs cI 2616, fol. 124r: Fibonacci-Zahlen am Rand der „Kaninchenaufgabe“

In seinem Rechenbuch Liber abbaci (nicht erhaltene Erstfassung 1202, erhaltene 2. Fassung nicht vor 1220), einem umfangreichen arithmetischen und algebraischen Lehrwerk über das Rechnen mit den indo-arabischen Ziffern, kommt der italienische Mathematiker Leonardo da Pisa, genannt „Fibonacci“, kurz auf die später nach ihm benannte Fibonacci-Folge zu sprechen. Fibonacci führt die Zahlenfolge vor (2, 3, 5, 8 … bis 377) und weist darauf hin, dass sich jedes Glied der Reihe (ab dem dritten) durch Summierung der beiden vorhergehenden Reihenglieder errechnen lässt. Eine weitere Beschäftigung mit dieser Folge findet sich bei ihm nicht, das heißt der Zusammenhang zum Goldenen Schnitt wird von ihm nicht dargestellt. Dass ihm allerdings der (erst später so genannte) Goldene Schnitt bekannt und in der Tradition Euklids ein Begriff war, zeigt sich gegen Ende seines Werks bei einer algebraischen Aufgabe, in der es (in moderner Formulierung wiedergegeben) darum geht $a$ und $b$ zu finden mit $10=a+b$ und ${\tfrac {a}{b}}+{\tfrac {b}{a}}={\sqrt {5}}$. Hierzu weist Fibonacci darauf hin, dass im Fall von $a>b$ die Proportion $10:a=a:b$ gilt, 10 also von $a$ und $b$ im Verhältnis des Goldenen Schnittes geteilt wird („et scis, secundum hanc diuisionem, 10 diuisa esse media et extrema proportione; quia est sicut 10 ad maiorem partem, ita maior pars ad minorem“). Aber auch hier stellt er den Zusammenhang zum Goldenen Schnitt nicht her.

Renaissance

Der vitruvianische Mensch, Leonardo da Vinci, 1492, Proportionsstudie nach Vitruv

Die Entdeckung, dass sich bei Teilung eines Gliedes der Fibonacci-Folge durch das vorhergehende Reihenglied als Näherungswert $\Phi$ ergibt, wurde lange Zeit Johannes Kepler zugeschrieben, konnte jedoch Ende des 20. Jahrhunderts schon in einer handschriftlichen Anmerkung nachgewiesen werden, mit der ein mutmaßlich aus Italien stammender Leser in der ersten Hälfte des 16. Jahrhunderts Euklids Theorem II.11 in der Euklid-Ausgabe Paciolis von 1509 kommentierte:

“Sit linea ab 233 pedum, divisa ut docet 11 huius in duo inaequalia in puncto h et sit bh portio eius maior 144 et ha portio eius minor 89. ducatur ab in ha et perveniunt 20737 et bh in se et perveniunt 20736. et sic cognosces quod in mutationibus non est laborandum quid impossibile est numerum ita dividi ut ista 11 proponit. similiter accidit si linea 13 pedum dividatur in lineam 8 pedum, et lineam 5.”

„Eine Gerade ab von 233 Fuß sei so, wie es Theorem 11 hier vorführt, an einem Punkt h in zwei ungleiche Teile geteilt, und dabei sei bh sein größerer Teil mit 144 und ha sein kleinerer Teil mit 89. ab sei multipliziert mit ha, und es ergeben sich 20737, und bh multipliziert mit sich selbst, so ergeben sich 20736. Und daran magst du erkennen, dass man sich nicht mit Ersetzungen abzumühen braucht, um zu zeigen, dass es unmöglich ist, die Zahl so zu teilen, wie es hier Theorem 11 vorführt. Das gleiche ergibt sich, wenn eine Gerade von 13 Fuß in eine Gerade von 8 und eine von 5 Fuß geteilt wird.“

Der Herausgeber dieser Euklid-Ausgabe, der Franziskaner Luca Pacioli di Borgo San Sepolcro (1445–1514), der an der Universität Perugia Mathematik lehrte, hatte sich intensiv mit dem Goldenen Schnitt befasst. Er nannte diese Streckenteilung „vermutlich als erster […] divina proportio (göttliches Verhältnis)“, was sich auf Platons Identifizierung der Schöpfung mit den fünf platonischen Körpern bezog, zu deren Konstruktion der Goldene Schnitt ein wichtiges Hilfsmittel darstellt. Sein gleichnamiges Werk De divina proportione von 1509 besteht aus drei unabhängigen Büchern. Bei dem ersten handelt es sich um eine rein mathematische Abhandlung, die jedoch keinerlei Bezug zur Kunst und Architektur herstellt. Das zweite ist ein kurzer Traktat über die Schriften des Römers Vitruv aus dem 1. Jahrhundert v. Chr. zur Architektur, in denen Vitruv die Proportionen des menschlichen Körpers als Vorlage für Architektur darstellt. Dieses Buch enthält eine Studie von Leonardo da Vinci (1452–1519) über den vitruvianischen Menschen. Das Verhältnis der Seitenlänge des den Menschen umgebenden Quadrats zum Radius des umgebenden Kreises – nicht das Verhältnis der Proportionen des Menschen selbst – in diesem berühmten Bild entspricht mit einer Abweichung von 1,7 % dem Goldenen Schnitt, der jedoch im zugehörigen Buch gar nicht erwähnt wird. Darüber hinaus würde diese Abweichung bei einem konstruktiven Verfahren nicht zu erwarten sein.

Ein Kepler-Dreieck ist ein rechtwinkliges Dreieck, das durch drei Quadrate gebildet werden kann, deren Flächeninhalte sich in geometrischer Progression $1:\varphi :\varphi ^{2}$, wie der Goldene Schnitt verhalten.

Im Oktober 1597 stellte Johannes Kepler in einem Brief an seinen früheren Tübinger Professor Michael Maestlin die Frage, warum es nur eine einzige mögliche Lösung für die Aufgabe gebe, ein rechtwinkliges Dreieck zu konstruieren, bei dem das Verhältnis der kürzeren zur längeren Seite dem der längeren zur Hypotenuse entspricht (Kepler-Dreieck). Auf das Original dieses Briefes notierte Maestlin eine Berechnung, die die Hypotenuse einmal mit 10 und einmal mit 10.000.000, und für den letzteren Fall dann die längere Seite mit 7.861.514 und die kürzeste Seite mit 6.180.340 beziffert. Das entspricht einer bis auf die sechste Nachkommastelle genauen (und bis zur fünften korrekten) Angabe des Goldenen Schnittes und ist nach den älteren sexagesimalen Berechnungen der Antike die erste bekannte dezimale Angabe dieser Art.

Seit dem 18. Jahrhundert

Populär wurde der Begriff Goldener Schnitt erst in der ersten Hälfte des 19. Jahrhunderts, obwohl die mathematischen Prinzipien schon seit der Antike bekannt waren. Der Begriff Goldene Zahl stammt aus dieser Zeit, noch 1819 wird dieser Begriff mit dem Meton-Zyklus in einem der griechischen Kalendersysteme in Verbindung gebracht. In der deutschen Literatur sind bereits Anfang des 18. Jahrhunderts vereinzelt Hinweise auf eine sinngemäße bzw. wortwörtliche Form des Begriffes „Goldener Schnitt“ zu finden. Erst ab dem zweiten Viertel des 19. Jahrhunderts war er weiter verbreitet. Die folgenden Beispiele aus der deutschen Literatur verweisen auf den Begriff in ähnlicher Art und Weise.

1717 wurde der Begriff Goldener Schnitt sinngemäß von M. Johann Wentzel Kaschube in seinem Werk Cursus mathematicus … verwendet. Er beschreibt darin eine geometrische Aufgabe (Näheres im Abschnitt Konstruktionsverfahren), deren Lösung dieses besondere Teilungsverhältnis verlangt. Am Schluss der Aufgabe §.35. ist zu lesen: „Die Alten hissen [sc. hießen] diesen Schnitt den Goldenen.“ Zu jener Zeit fand das Teilungsverhältnis des Goldenen Schnittes auch in der Akustik im Zusammenhang mit Verhältnissen der Saitenlänge Anwendung. Diese Form der Saitenteilung – so Ernst Florens Friedrich Chladni 1802 in Die Akustik unter Die geometrische Theilung  – wollte auch Gottfried Wilhelm Leibniz. Zwar lassen sich damit nicht Tonhöhenabstände, sprich Intervalle finden, „desto brauchbarer ist sie aber, wie im folgenden Abschnitte wird gezeigt werden, zu gewissen nothwendigen Abänderungen derselben.“ Chladni leitete die Tonverhältnisse also nicht aus den Saitenlängen ab, sondern aus den Verhältnissen der Schwingungszahlen. Bezüglich des Goldenen Schnitts merkt Chladni an: „Es ist diese Theilung eben dasselbe, was von einigen ältern Mathematikern, die besondere Eigenschaften darin finden wollten, sectio aurea, oder sectio divina [der Goldene Schnitt oder göttliche Schnitt] genennt worden ist.“

Etwas mehr als fünfzig Jahre später wurden die Proportionen des menschlichen Körpers wissenschaftlich mit denen des Goldenen Schnittes verglichen. Adolf Zeising benennt 1854 in Neue Lehre von den Proportionen des menschlichen Körpers … das Ergebnis der „Maassbestimmungen […] kurzweg, das Proportionalgesetz“. Er beschreibt es als einen geometrischen Weg zur proportionalen Teilung einer Linie $ab$ und stellt fest:

„Die Mathematiker nennen die hier erörterte Theilung einer gegebenen Linie die ‚Theilung im äussern und mittlern Verhältnisse‘ oder ‚den goldnen Schnitt‘. Der Grund der letztern Benennung ist mir nicht bekannt; doch rührt sie wahrscheinlich daher, weil man die ausserordentlichen Vorzüge des Verhältnisses, welches man durch diese Theilung gewinnt, und die Vollkommenheit der durch dieses Verhältniss gebildeten Proportion mit richtigem Blicke erkannt hat.“

– Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers, […]

Gustav Theodor Fechner, ein Begründer der experimentellen Psychologie, stellte 1876 bei Untersuchungen mit Versuchspersonen anhand von Rechtecken in der Tat eine Präferenz für den Goldenen Schnitt fest. Die Ergebnisse bei der Streckenteilung und bei Ellipsen fielen jedoch anders aus. Neuzeitliche Untersuchungen zeigen, dass das Ergebnis solcher Experimente stark vom Kontext der Darbietung abhängt. Fechner fand ferner bei Vermessungen von Bildern in verschiedenen Museen Europas, dass die Seitenverhältnisse im Hochformat im Mittel etwa 4:5 und im Querformat etwa 4:3 betragen und sich damit deutlich vom Goldenen Schnitt unterscheiden.

Bis ins späte 20. Jahrhundert erhielt der Goldene Schnitt auf viele Art und Weise seine Aufmerksamkeit ausschließlich in der Makrowelt. Dann aber entdeckten Wissenschaftler bei Forschungen in der atomaren Welt überraschenderweise Gebilde mit mathematischen Kennwerten, die dem Goldenen Schnitt gleichen. Die Forschungsergebnisse der beiden folgenden Beispiele fanden in den betreffenden Wissenschaftsbereichen hohe internationale Anerkennung.

Als Erster erkannte Dan Shechtman mit seinen Kollegen 1982 bei Röntgenstrukturanalysen Beugungsbilder mit fünfzähliger Symmetrie in Quasikristallen der Festkörperphysik. Für diese Entdeckung bekam Shechtman 2011 den Nobelpreis für Chemie. Näheres ist im Abschnitt Quasikristalle enthalten. Die erstmalige Entdeckung des Goldenen Schnitts in fester Materie gelang Forschern des Helmholtz-Zentrums Berlin für Materialien und Energie (HZB) im Kristall aus Kobalt-Niobat (veröffentlicht in der Zeitschrift Science, Januar 2010). Näheres ist im Abschnitt Kobalt-Niobat enthalten.

Grundlegende mathematische Eigenschaften

Irrationalität und Algebraizität

Der Goldene Schnitt ist eine irrationale Zahl; das heißt, er lässt sich nicht als Bruch zweier ganzer Zahlen darstellen. Weiter bedeutet es, dass die Dezimalentwicklung kein periodisches Muster aufzeigt. Die ersten 50 Nachkommastellen des Goldenen Schnittes sind gegeben durch

$\Phi =1{,}61803\,\,39887\,\,49894\,\,84820\,\,45868\,\,34365\,\,63811\,\,77203\,\,09179\,\,80576\,\,\ldots$.

Seit dem 14. Februar 2021 sind 10 Billionen (10 × 10¹²) Nachkommastellen von $\Phi$ berechnet und verifiziert worden. Zudem gelten bereits 20 Billionen Stellen als berechnet, jedoch noch nicht als verifiziert.

Der Grund, warum $\Phi ={\tfrac {1+{\sqrt {5}}}{2}}$ irrational ist, verbirgt sich hinter der Irrationalität von ${\sqrt {5}}$.

Der Beweis, dass ${\sqrt {5}}$ irrational sein muss, erfolgt analog zum Beweis der Irrationalität der Wurzel aus 2 bei Euklid. Dazu ist es nützlich, das Gesetz der bis auf die Reihenfolge eindeutigen Zerlegbarkeit natürlicher Zahlen in Primzahlen zu kennen. Nimmt man an, es sei ${\tfrac {p}{q}}={\sqrt {5}}$ mit einem vollständig gekürzten Bruch ${\tfrac {p}{q}}$ mit positiven ganzen Zahlen $p,q$, so gilt bereits

$p^{2}=5q^{2}$.

Es ist also $p^{2}$ und ergo auch $p$ durch $5$ teilbar, da $5$ eine Primzahl ist. Damit besitzt $p$ also den Primteiler $5$,und dieser taucht bei $p^{2}$ in gerader Anzahl auf, da sich beim Quadrieren alle Primfaktoren verdoppeln. Da $p$ und $q$ teilerfremd sind – es ist ${\tfrac {p}{q}}$ nach Annahme vollständig gekürzt – taucht der Primfaktor $5$ nirgends in $q$ auf. Ergo taucht er nur einmal in $5q^{2}$ auf. Dies ist ein Widerspruch zur eindeutigen Primfaktorzerlegung, die besagt, dass auf beiden Seiten gleich viele Fünfen auftauchen müssen, aber $1$ ist keine gerade Zahl. Zu guter Letzt muss dann auch ${\tfrac {1}{2}}+{\tfrac {\sqrt {5}}{2}}$ irrational sein, da irrationale Zahlen im Produkt mit rationalen Zahlen (außer 0) und in Summe mit rationalen Zahlen wieder irrational sind.

Die Goldene Zahl ist ferner eine algebraische Zahl vom Grad 2, insbesondere kann sie mit Zirkel und Lineal konstruiert werden. Damit grenzt sie sich von anderen berühmten Konstanten, wie der Kreiszahl $\pi$ oder der Eulerschen Zahl $\mathrm {e}$, ab, die transzendent, und damit niemals Nullstelle eines nicht-konstanten Polynoms mit rationalen Koeffizienten sind.

Zusammenhang mit den Fibonacci- und Lucas-Zahlen

Verhältnisse aufeinanderfolgender
Fibonacci-Zahlen

$f_{n}$	$f_{n+1}$	${\frac {f_{n+1}}{f_{n}}}$	Abweichung zu $\Phi$ in %
01	01	= 1,0000	−38,0000
01	02	= 2,0000	+23,0000
02	03	= 1,5000	−7,300
03	05	≈ 1,6667	+3,000
05	08	= 1,6000	−1,100
08	13	= 1,6250	+0,430
13	21	≈ 1,6154	−0,160
21	34	≈ 1,6190	+0,063
34	55	≈ 1,6176	−0,024
55	89	≈ 1,6182	0+0,0091
89	144	≈ 1,6180	0−0,0035
144	233	≈ 1,6181	0+0,0013

In einem engen Zusammenhang zum Goldenen Schnitt steht die unendliche Zahlenfolge der Fibonacci-Zahlen (siehe unten die Abschnitte Mittelalter und Renaissance):

$1,1,2,3,5,8,13,21,34,55,89,144,233,\ldots$.

Die jeweils nächste Zahl in dieser Folge wird als Summe der beiden vorangehenden erhalten. Das Verhältnis zweier aufeinanderfolgender Zahlen der Fibonacci-Folge strebt gegen den Goldenen Schnitt (siehe Tabelle). Das rekursive Bildungsgesetz $f_{n+1}=f_{n}+f_{n-1}$ bedeutet nämlich

${\frac {f_{n+1}}{f_{n}}}={\frac {f_{n}+f_{n-1}}{f_{n}}}=1+{\frac {f_{n-1}}{f_{n}}}$.

Sofern dieses Verhältnis gegen einen Grenzwert $x$ konvergiert, muss für diesen gelten

$x=1+{\frac {1}{x}}$.

In der Tat lässt sich daraus

$\lim _{n\to \infty }{\frac {f_{n+1}}{f_{n}}}=\Phi$

folgern. Die Glieder der Fibonacci-Folge $f_{n}$ lassen sich für alle $n\in \mathbb {N}$ über die Formel von Binet berechnen:

$f_{n}={\frac {1}{\sqrt {5}}}\left(\Phi ^{n}-\left(-{\tfrac {1}{\Phi }}\right)^{n}\right)$.

Diese Formel liefert die für die Fibonacci-Folge veranschlagten Anfangswerte $f_{0}=0$ und $f_{1}=1$ und erfüllt die rekursive Gleichung $f_{n+1}=f_{n}+f_{n-1}$ für alle $n$ mit $n\geq 1$.

Ähnlich gilt

$L_{n}=\Phi ^{n}+\left(-{\tfrac {1}{\Phi }}\right)^{n}=\Phi ^{n}+(1-\Phi )^{n}$

für die $n$-te Lucas-Zahl. Allgemeiner ist jede komplexe Folge $(F_{n})_{n\in \mathbb {Z} }$ mit $F_{n}=F_{n-1}+F_{n-2}$ von der Form $F_{n}=a\Phi ^{n}+b(-\Phi ^{-1})^{n}$, wobei $a,b$ komplexe Zahlen sind, und umgekehrt.

Kettenbruchentwicklung

Da der Goldene Schnitt irrational ist, stellt sich die Frage, wie gut er sich durch rationale Zahlen annähern lässt. Grundsätzlich konnte gezeigt werden, dass es für eine beliebige irrationale Zahl $x$ stets unendlich viele rationale Zahlen ${\tfrac {p}{q}}$ gibt, so dass

$\left|x-{\frac {p}{q}}\right|<{\frac {1}{{\sqrt {5}}q^{2}}}$.

Dieses Resultat ist fundamental im Gebiet der diophantischen Approximation. Erhöht sich der Nenner $q$, sind grundsätzlich auch bessere Annäherungen möglich, wie das sogar quadratische Abklingen der rechten Seite zeigt. Bemerkenswert ist die Konstante ${\sqrt {5}}$, die optimal gewählt ist, also nicht weiter vergrößert werden kann. Grund dafür ist der Goldene Schnitt, der (zusammen mit zu ihm äquivalenten Zahlen) die Eigenschaft hat, dass für alle $C>{\sqrt {5}}$ nur endlich viele rationale Annäherungen mit

$\left|\Phi -{\frac {p}{q}}\right|<{\frac {1}{Cq^{2}}}$

existieren. Für irrationale Zahlen, die nicht zu $\Phi$ äquivalent sind, lässt sich die Konstante $C$ größer als ${\sqrt {5}}$ wählen (nämlich mit Wert $2{\sqrt {2}}$ (Satz von Hurwitz)). Der Goldene Schnitt gehört also unter den irrationalen Zahlen zu den am schlechtesten durch rationale Zahlen approximierbaren. Da seine Kettenbruchentwicklung überdies nur Einsen enthält, ist er in diesem Sinn die „irrationalste aller Zahlen“.

Der mathematische Beweis der oberen Aussage fußt auf sogenannten Kettenbrüchen. Jede reelle Zahl lässt sich (im Wesentlichen eindeutig) durch einen Kettenbruch darstellen. Bricht man diesen nach endlich vielen Schritten ab, ergibt sich eine „besonders gute“ rationale Annäherung an diese Zahl. Für die Goldene Zahl gilt nun aber $\Phi =1+{\tfrac {1}{\Phi }}$, woraus sich durch wiederholte Anwendung ergibt:

$\Phi =1+{\frac {1}{\Phi }}=1+{\frac {1}{1+{\frac {1}{\Phi }}}}=\dotsb =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {\cdots }{\dotsb +{\cfrac {1}{\Phi }}}}}}}}}}$.

Bricht man die Kettenbruchentwicklung ab, erhält man stets einen Bruch aus zwei aufeinanderfolgenden Fibonacci-Zahlen. Weil im Kettenbruch lediglich Einsen auftauchen – die kleinste natürliche Zahl –, nähert sich dieser Kettenbruch mit der „minimal möglichen Geschwindigkeit“ der Goldenen Zahl an. Im Vergleich ist der Kettenbruch zur Kreiszahl $\pi$ – ebenfalls irrational – deutlich schneller konvergent.

In der Theorie der dynamischen Systeme werden Zahlen, deren unendliche Kettenbruchdarstellung ab einer Stelle nur noch Einsen enthält, als „noble Zahlen“ bezeichnet. In diesem Kontext wird der Goldene Schnitt als „nobelste“ aller noblen Zahlen bezeichnet.

Geometrische Aussagen

Konstruktionsverfahren

Als Konstruktionsverfahren werden nach den Postulaten des Euklid nur diejenigen Verfahren akzeptiert, die sich auf die Verwendung von Zirkel und Lineal (ohne Skala) beschränken. Für die Teilung einer Strecke im Verhältnis des Goldenen Schnittes gibt es eine Fülle derartiger Verfahren, von denen im Folgenden exemplarisch nur einige erwähnt werden. Unterschieden wird dabei eine innere und äußere Teilung. Bei der äußeren Teilung wird der in der Verlängerung der Ausgangsstrecke außen liegende Punkt gesucht, der die vorhandene Strecke zum (größeren) Teil des Goldenen Schnittes macht. Der Goldene Schnitt stellt dabei einen Spezialfall der harmonischen Teilung dar. Aufgeführt werden im Folgenden auch zwei moderne, von Künstlern gefundene Konstruktionen.

Innere Teilung

Klassische innere Teilung	Klassisches Verfahren mit innerer Teilung nach Heron von Alexandria, das wegen seiner Einfachheit beliebt ist: Errichte auf der Strecke AB im Punkt B eine Senkrechte der halben Länge von AB mit dem Endpunkt C. Der Kreis um C mit dem Radius CB schneidet die Verbindung AC im Punkt D. Der Kreis um A mit dem Radius AD teilt im Punkt S die Strecke AB im Verhältnis des Goldenen Schnittes. Dies kann wie folgt eingesehen werden: Über den Satz des Pythagoras ergibt sich für die Länge der Hypotenuse der Wert |AC|$={\sqrt {1^{2}+\left({\tfrac {1}{2}}\right)^{2}}}$|AB|$={\tfrac {\sqrt {5}}{2}}$|AB|. Subtrahiert man von dieser die Länge |DC|$={\tfrac {1}{2}}$AB, verbleibt gerade AD$={\tfrac {{\sqrt {5}}-1}{2}}$|AB|$=\Phi ^{-1}$|AB|$=$|AS|. Aus den algebraischen Vorüberlegungen ist nun bekannt, dass dies das Verhältnis der stetigen Teilung ist.
	Innere Teilung nach Euklid: Goldener Schnitt, innere Teilung nach Euklid 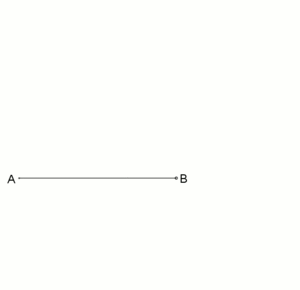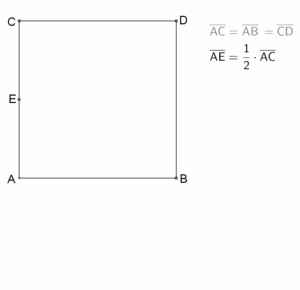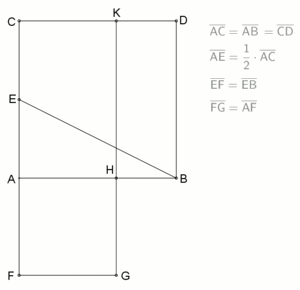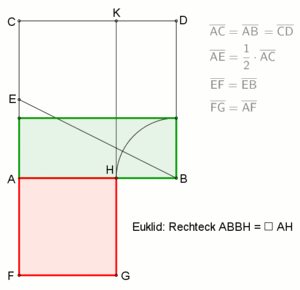Johann Friedrich Lorenz beschrieb im Jahr 1781 in seinem Buch Euklids Elemente folgende Aufgabenstellung von Euklid: „Eine gegebne gerade Linie, AB, so zu schneiden, daß das Rectangel aus der Ganzen und Einem der Abschnitte, dem Quadrat des anderen Abschnitts gleich sey.“ Das Ergebnis der nebenstehenden Animation zeigt, die Strecke AB ist in einem Verhältnis geteilt, das als Goldener Schnitt mit innerer Teilung bezeichnet wird. Als Darstellung dieses Verfahrens hat sich eine vereinfachte Konstruktion, siehe linkes Bild, bewährt: Errichte auf der Strecke AB im Punkt A eine Senkrechte der halben Länge von AB mit dem Endpunkt C. Der Kreis um C mit dem Radius CB schneidet die Verlängerung von AC im Punkt D. Der Kreis um A mit dem Radius AD teilt im Punkt S die Strecke AB im Verhältnis des Goldenen Schnittes.
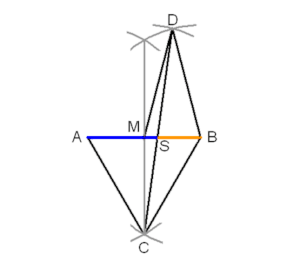
	Konstruktion nach dem österreichischen Künstler Kurt Hofstetter, die dieser 2005 im Forum Geometricorum publizierte: Halbiere die Strecke AB in M durch Streckensymmetrale mit Radius AB und konstruiere dabei ein gleichseitiges Dreieck ABC mit der Seitenlänge AB und C unterhalb von AB. Konstruiere ein gleichschenkliges Dreieck MBD mit Schenkellänge AB über der Grundlinie MB. Die Strecke CD teilt im Punkt S die Strecke AB im Verhältnis des Goldenen Schnittes.

Äußere Teilung

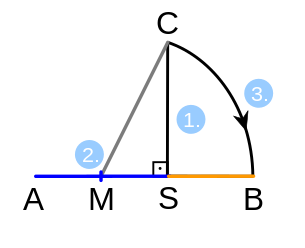
Klassisches Verfahren mit äußerer Teilung nach Euklid: Äußere Teilung nach Eklid „Die Seiten eines demselben Kreis einbeschriebenen gleichseitigen Sechsecks und eines gleichseitigen Zehnecks zusammen ergeben eine Strecke, die in stetiger Teilung geteilt ist, wobei die Seite des Sechsecks der größere Teil ist.“ Die nebenstehende Animation (am Ende mit 30 s Pause) zeigt prinzipiell die hierfür erforderlichen Konstruktionsschritte. Die abschließend eingetragenen strichlierten Linien sowie die Punkte K und L sind nicht Teil der Lösung nach Euklid. Sie sollen lediglich den konstruktiven Weg zur folgenden Vereinfachung verdeutlichen. Die Darstellung im linken Bild hat sich als vereinfachte Konstruktion bewährt: Errichte auf der Strecke AS im Punkt S eine Senkrechte der Länge AS mit dem Endpunkt C. Konstruiere die Mitte M der Strecke AS. Der Kreis um M mit dem Radius MC schneidet die Verlängerung von AS im Punkt B. S teilt AB im Verhältnis des Goldenen Schnittes. Dieses Verfahren wird für die Konstruktion des Fünfecks bei gegebener Seitenlänge verwendet.

Konstruktion nach dem amerikanischen Künstler George Odom, die dieser 1982 entdeckte: Konstruiere ein gleichseitiges Dreieck. Konstruiere den Umkreis, also den Kreis, der durch alle Ecken des Dreiecks verläuft. Halbiere zwei Seiten des Dreiecks in den Punkten A und S. Die Verlängerung von AS schneidet den Kreis im Punkt B. S teilt AB im Verhältnis des Goldenen Schnittes. Die algebraische Herleitung ist im Unterabschnitt Im Umkreis eines gleichseitigen Dreiecks beschrieben.

Im Fünfeck und im Pentagramm

Goldener Schnitt im Fünfeck und Pentagramm

Regelmäßiges Fünfeck und Pentagramm bilden jeweils eine Grundfigur, in der das Verhältnis des Goldenen Schnittes wiederholt auftritt. Die Seite eines regelmäßigen Fünfecks befindet sich im Goldenen Schnitt zu seinen Diagonalen. Die Diagonalen untereinander wiederum teilen sich ebenfalls im Goldenen Verhältnis, das heißt, $\mathrm {\overline {AD}}$ verhält sich zu $\mathrm {\overline {BD}}$ wie $\mathrm {\overline {BD}}$ zu $\mathrm {\overline {CD}}$. Der Beweis dazu nutzt die Ähnlichkeit geeignet gewählter Dreiecke.

Das Pentagramm, eines der ältesten magischen Symbole der Kulturgeschichte, steht in einer besonders engen Beziehung zum Goldenen Schnitt. Zu jeder Strecke und Teilstrecke im Pentagramm findet sich ein Partner, der mit ihr im Verhältnis des Goldenen Schnittes steht. In der Abbildung sind alle drei möglichen Streckenpaare jeweils blau (längere Strecke) und orange (kürzere Strecke) markiert. Sie lassen sich über das oben beschriebene Verfahren der stetigen Teilung nacheinander erzeugen. Im Prinzip ist es damit in das verkleinerte Pentagramm fortsetzbar, das in das innere Fünfeck gezeichnet werden könnte, und damit in alle weiteren. Stünden die beiden Strecken in einem Verhältnis ganzer Zahlen, müsste dieses Verfahren der fortgesetzten Subtraktion irgendwann Null ergeben und damit abbrechen. Die Betrachtung des Pentagramms zeigt aber anschaulich, dass das nicht der Fall ist. Eine Weiterentwicklung dieser Geometrie findet sich bei der Penrose-Parkettierung.

Für den Beweis, dass es sich um den Goldenen Schnitt handelt, beachte man, dass neben den vielen Strecken, die aus offensichtlichen Symmetriegründen gleich lang sind, auch $|{\overline {\mathrm {CD} }}|=|{\overline {\mathrm {CC'} }}|$ gilt. Ursache ist, dass das Dreieck $\mathrm {DCC^{\prime }}$ zwei gleiche Winkel besitzt, wie durch Parallelverschiebung der Strecke $\mathrm {\overline {CC^{\prime }}}$ erkannt werden kann, und daher gleichschenklig ist. Nach dem Strahlensatz gilt:

${\frac {|{\overline {\mathrm {AB} }}|}{|{\overline {\mathrm {BB'} }}|}}={\frac {|{\overline {\mathrm {AC} }}|}{|{\overline {\mathrm {CC'} }}|}}$

Wird $|{\overline {\mathrm {AC} }}|=|{\overline {\mathrm {AB} }}|+|{\overline {\mathrm {BC} }}|$ ersetzt und die Gleichheit der auftretenden Teilstücke beachtet, so wird genau die obige Definitionsgleichung für den Goldenen Schnitt erhalten.

Im gleichschenkligen Dreieck

Goldener Schnitt im gleichschenkligen Dreieck

In einem gleichschenkligen Dreieck $\mathrm {ABC}$, dessen Grundseite $\mathrm {\overline {AB}}$ längengleich zu der Höhe $\mathrm {\overline {DC}}$ ist, teilt der innerhalb des Dreiecks liegende Schnittpunkt $\mathrm {F}$ des Inkreises mit der Höhe diese im Goldenen Schnitt.

Ohne Beschränkung der Allgemeinheit kann $|{\overline {\mathrm {AB} }}|=|{\overline {\mathrm {CD} }}|$ angenommen werden. Die rechtwinkligen Dreiecke $\mathrm {MBE}$ und $\mathrm {DBM}$ sind kongruent, da sie in zwei Seiten und dem (rechten) Gegenwinkel der größeren Seite übereinstimmen. Es gilt $|{\overline {\mathrm {DB} }}|=|{\overline {\mathrm {BE} }}|=1$ und damit $|{\overline {\mathrm {CE} }}|=|{\overline {\mathrm {CB} }}|-|{\overline {\mathrm {BE} }}|={\sqrt {5}}-1$. Nach dem Satz des Pythagoras gilt $|{\overline {\mathrm {BC} }}|^{2}=2^{2}+1^{2}=5\Leftrightarrow |{\overline {\mathrm {BC} }}|={\sqrt {5}}$ in dem rechtwinkligen Dreieck $\mathrm {DBC}$. Ebenfalls nach dem Satz des Pythagoras gilt in dem rechtwinkligen Dreieck $\mathrm {CME}$: $|{\overline {\mathrm {CE} }}|^{2}=(2-r)^{2}-r^{2}\Leftrightarrow ({\sqrt {5}}-1)^{2}=4-4r\Leftrightarrow r={\frac {{\sqrt {5}}-1}{2}}=\Phi ^{-1}$. Mit $d=2r$ folgt hieraus $\Phi =2:d$ = (Höhe von ABC) : (Durchmesser des Inkreises von ABC), was zu zeigen war.

Im Umkreis eines gleichseitigen Dreiecks

Bestimmung des Goldenen Schnitts nach dem Verfahren von George Odom

In dem gleichseitigen Dreieck $\mathrm {ABC}$ schneidet die durch $\mathrm {E}$ und $\mathrm {F}$ verlaufende Parallele zu ${\overline {\mathrm {AB} }}$ den Umkreis in $\mathrm {D}$ und $\mathrm {G}$. Ist ${\overline {\mathrm {AE} }}={\overline {\mathrm {EC} }}$, dann teilt $\mathrm {F}$ die Strecke ${\overline {\mathrm {EG} }}$ im Goldenen Schnitt.

Aus den Eigenschaften eines gleichseitigen Dreiecks und aus dem Strahlensatz folgen unmittelbar die Längengleichheiten

$|{\overline {\mathrm {AE} }}|=|{\overline {\mathrm {BF} }}|=|{\overline {\mathrm {CE} }}|=|{\overline {\mathrm {CF} }}|=|{\overline {\mathrm {EF} }}|=a$ und $|{\overline {\mathrm {AB} }}|=2a$.

Nach dem Sehnensatz gilt:

 $a^{2}=b(a+b)\Leftrightarrow {\frac {a^{2}}{b}}=a+b\Leftrightarrow \left({\frac {a}{b}}\right)^{2}={\frac {a}{b}}+1$

$\Leftrightarrow \left({\frac {a}{b}}\right)^{2}-\left({\frac {a}{b}}\right)-1=0\Leftrightarrow {\frac {a}{b}}=\Phi$

Somit teilt $\mathrm {F}$ die Strecke ${\overline {\mathrm {EG} }}$ im Goldenen Schnitt.

Im Quader

Goldener Schnitt im Quader ${\frac {a}{b}}=\Phi$ und ${\frac {c}{b}}=\Phi ^{-1}$

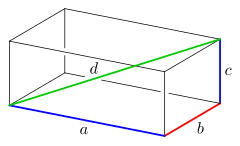
Für einen Quader mit den Kantenlängen $\mathrm {a}$, $\mathrm {b}$ und $\mathrm {c}$, der Raumdiagonalenlänge $\mathrm {d}$ und dem Volumen $\mathrm {V}$ gelte $a>c$, $b=1$, $d=2$ und $V=1$.

Dann gilt für den Goldenen Schnitt $\Phi$ das Verhältnis

$\Phi ={\frac {a}{b}}={\frac {a+b}{a}}={\frac {1+{\sqrt {5}}}{2}}$.

Aus der Volumengleichung $a\cdot b\cdot c=1$ folgt wegen $b=1$

$a\cdot c=1$. (1)

Da die Raumdiagonale die Länge 2 hat, gilt

${\sqrt {a^{2}+1^{2}+c^{2}}}=2\Leftrightarrow a^{2}+c^{2}=3$. (2)

Aus (1) und (2) erhält man $a^{2}+a^{-2}=3$.

Die Lösungen mit positivem Wert sind $a=\Phi$ oder  $a=\Phi ^{-1}$ und damit analog $c=\Phi$ oder $c=\Phi ^{-1}$.

Wegen $a>c$ kommen nur $a=\Phi$ und $c=\Phi ^{-1}$ in Betracht. Damit ergibt sich

${\frac {a}{b}}=\Phi$  und  ${\frac {c}{b}}=\Phi ^{-1}$

Im Ikosaeder

Die 3 Goldenen Rechtecke (hellgrün, grün, lila) bilden mit ihren jeweils 4 Ecken die 12 Ecken (9 hier sichtbar) eines Ikosaeders

Die 12 Ecken des Ikosaeders bilden die Ecken von 3 gleich großen, senkrecht aufeinanderstehenden Rechtecken mit gemeinsamem Mittelpunkt und mit den Seitenverhältnissen des Goldenen Schnittes. Die zwölf Ecken eines Ikosaeders sind also die zwölf Ecken dreier goldener Rechtecke, die paarweise aufeinander senkrecht stehen. Diese Anordnung der 3 Rechtecke wird auch Goldener-Schnitt-Stuhl genannt. Weil der Ikosaeder zum Pentagondodekaeder dual ist, bilden die 12 Mittelpunkte der Fünfecke ebenfalls die Ecken eines Goldener-Schnitt-Stuhls.

Ferner kann in ein gegebenes Oktaeder ein Ikosaeder so einbeschrieben werden, dass dessen Ecken die Kanten des Oktaeders im Goldenen Schnitt teilen.

Goldenes Rechteck und Goldenes Dreieck

Ein Rechteck, dessen Seitenverhältnis dem Goldenen Schnitt entspricht, wird als Goldenes Rechteck benannt; ebenso heißt ein gleichschenkliges Dreieck, bei dem zwei Seiten in diesem Verhältnis stehen, Goldenes Dreieck.

• Zum Vergleich von Rechtecksproportionen siehe Abschnitt Vergleich mit anderen prominenten Seitenverhältnissen.
• Ein Goldenes Dreieck ist Inhalt der Methode äußere Teilung im Abschnitt Konstruktionsverfahren, äußere Teilung

Goldener Winkel

Der Goldene Winkel ist der kleinere Kreiswinkel $b$, dessen Verhältnis zum größeren Winkel ($a:b$) dem Goldenen Schnitt entspricht.

Blattstand einer Pflanze mit einem Blattabstand nach dem Goldenen Winkel

Der Goldene Winkel wird erhalten, wenn der Vollwinkel im Goldenen Schnitt geteilt wird. Dies führt auf den überstumpfen Winkel ${\tfrac {2\pi }{\Phi }}\approx 3{,}88\approx 222{,}5^{\circ }$ Gewöhnlich wird aber seine Ergänzung zum Vollwinkel, $2\pi -{\tfrac {2\pi }{\Phi }}\approx 2{,}40\approx 137{,}5^{\circ }$ als Goldener Winkel bezeichnet. Dies ist dadurch gerechtfertigt, dass Drehungen um $\pm 2\pi$ keine Rolle spielen und das Vorzeichen nur den Drehsinn des Winkels bezeichnet.

Durch wiederholte Drehung um den Goldenen Winkel entstehen immer wieder neue Positionen, etwa – wie im Bild vereinfacht dargestellt – für die Blattansätze (Näheres im Abschnitt Biologie).

Dabei zerlegen die ersten $n$ Positionen den Kreis in $n$ Ausschnitte. Diese $n$ Ausschnitte haben höchstens drei verschiedene Winkel. Im Fall einer Fibonacci-Zahl $n=f_{k}$ treten nur zwei Winkel ${\tfrac {2\pi }{\Phi ^{k-1}}},{\tfrac {2\pi }{\Phi ^{k}}}$ auf. Für $f_{k}<n<f_{k+1}$ tritt der Winkel ${\tfrac {2\pi }{\Phi ^{k+1}}}$ hinzu.

Betrachtet man für wachsendes $n$ fortfolgend die sich verfeinernden Zerlegungen des Kreises, so teilt die $(n+1)$-te Position stets einen der verbliebenen größten Ausschnitte, und zwar immer den im Verlauf der Teilungen zuerst entstandenen, das heißt den „ältesten“ Ausschnitt. Diese Teilung erfolgt im Goldenen Verhältnis, sodass, im Uhrzeigersinn gesehen, ein Winkel ${\tfrac {2\pi }{\Phi ^{l}}}$ mit geradem $l$ vor einem Winkel ${\tfrac {2\pi }{\Phi ^{l\pm 1}}}$ mit ungeradem $l\pm 1$ liegt.

Wenn wir den Ausschnitt mit dem Winkel ${\tfrac {2\pi }{\Phi ^{k}}}$ mit $w_{k}$ bezeichnen, so erhalten wir nacheinander die Kreiszerlegungen
$\ w_{0}$, $\ w_{2}w_{1}$, $\ w_{2}w_{2}w_{3}$, $\ w_{4}w_{3}w_{2}w_{3}$, $\ w_{4}w_{3}w_{4}w_{3}w_{3}$, $\ w_{4}w_{3}w_{4}w_{3}w_{4}w_{5}$, $\ w_{4}w_{4}w_{5}w_{4}w_{3}w_{4}w_{5}$, $\ w_{4}w_{4}w_{5}w_{4}w_{4}w_{5}w_{4}w_{5}$, $\ w_{6}w_{5}w_{4}w_{5}w_{4}w_{4}w_{5}w_{4}w_{5}$, $\ w_{6}w_{5}w_{4}w_{5}w_{6}w_{5}w_{4}w_{5}w_{4}w_{5}$ usw.

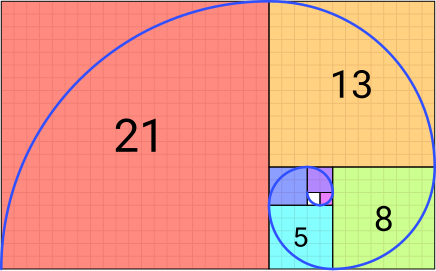
Goldene Spirale und Spira mirabilis

Beide Spiralen hängen mit dem Goldenen Schnitt zusammen. Sie sind nicht als Konstruktion mit Zirkel und Lineal darstellbar. Für eine Näherungskonstruktion bedarf es – wie im Folgenden erläutert – eines Goldenen Rechtecks bzw. eines Goldenen Dreiecks.

Goldene Spirale

Die Goldene Spirale, auch Bernoulli’sche Spirale genannt, ist ein Sonderfall der logarithmischen Spirale: Ihr Streckungsfaktor (siehe Zentrische Streckung) ist $\Phi$, die Zahl des Goldenen Schnitts. Sie lässt sich mittels rekursiver Teilung eines Goldenen Rechtecks in je ein Quadrat und ein weiteres, kleineres Goldenes Rechteck näherungsweise konstruieren. Ihr Radius ändert sich bei jeder 90°-Drehung um den Faktor $\Phi$.

Die Goldene Spirale lässt sich unter Verwendung von Polarkoordinaten durch

$\textstyle r(\theta )=\Phi ^{\frac {2\theta }{\pi }}$

parametrisieren. Die Idee von Polarkoordinaten ist hierbei, einen Punkt $\mathrm {P}$ in der Ebene durch seinen Abstand $r$ zum Ursprung und den mit der $x$-Achse eingeschlossen Winkel $\theta$ festzulegen. Dessen Polarkoordinaten sind dann $(r,\theta )$, und durch Wahl des Radius in Abhängigkeit vom sich verändernden Winkel $\theta$ lassen sich manche geometrische Figuren durch eine entsprechende Funktion $r(\theta )$ einfacher beschreiben als in klassischen kartesischen Koordinaten. Zu beachten ist, dass mehrfache Umdrehungen um den Ursprung, etwa in den Fällen $\theta _{0}=0$ (Ausgangslage), $\theta _{1}=2\pi$ (eine Volldrehung), $\theta _{2}=4\pi$ (zwei Volldrehungen) usw. unterschiedliche Radii hervorrufen können, was auch an der nicht-periodischen Figur der Spirale zu erkennen ist.

Eine brauchbare Näherung für die Goldene Spirale findet sich bereits bei Kepler. Man erhält diese Approximation, wenn man in die Quadrate Viertelkreise mit dem Radius der Seitenlänge des Quadrats einzeichnet. Dies ist im mittleren Bild illustriert. Im linken Bild wird die Güte dieser Approximation veranschaulicht.

• 
  Grün Annäherung durch Vierteilkreise (rechtes Bild); Rot Goldene Spirale; Gelb: Überlappungen.
• 
  Annäherung der Goldenen Spirale, unter Benutzung von Viertelkreisen und der Fibonacci-Folge $1,1,2,3,5,8,13,21,\ldots$
• 
  Goldene Spiralen sind selbstähnlich. Ihre Form wiederholt sich unendlich oft, wenn sie vergrößert wird.

Die Goldene Spirale ist unter den logarithmischen Spiralen durch die folgende Eigenschaft ausgezeichnet. Seien $P_{1},P_{2},P_{3},P_{4}$ vier auf der Spirale aufeinanderfolgende Schnittpunkte mit einer Geraden durch das Zentrum. Dann sind die beiden Punktepaare $P_{1},P_{4}$ und $P_{2},P_{3}$ harmonisch konjugiert, das heißt, für ihr Doppelverhältnis gilt:

$(P_{\theta },P_{\theta +3\pi };\ P_{\theta +\pi },P_{\theta +2\pi })={\frac {(-\Phi ^{6}-\Phi ^{4})(-\Phi ^{2}-1)}{(-\Phi ^{6}+\Phi ^{2})(+\Phi ^{4}-1)}}={\frac {-\Phi ^{2}}{(-\Phi ^{2}+1)^{2}}}=-1$

Spira mirabilis

Spira mirabilis generiert aus einem Goldenen Dreieck, Kurve mithilfe GeoGebra erzeugt, siehe Animation der Konstruktion

Die Spira mirabilis ist ebenfalls ein Sonderfall der logarithmischen Spirale: Ihr Streckungsfaktor ist $\Phi ^{-1}$, sprich der Kehrwert des Goldenen Schnitts. Sie benötigt für die Näherungskonstruktion die rekursive Teilung eines Goldenen Dreiecks in je ein gleichschenkliges stumpfwinkliges Dreieck und in ein weiteres, kleineres Goldenes Dreieck. Dies ist begründet durch eine sogenannte Drehstreckung $\sigma$. Sie enthält eine Drehung um ${\tfrac {-3\pi }{5}}$ (entspricht $-108^{\circ }$). Daraus ergibt sich eine Streckung mit dem Faktor $\Phi ^{-1}$.

Das nebenstehende Bild zeigt ein solches gleichschenkliges Dreieck $\mathrm {ABC}$ mit den Basiswinkeln $72^{\circ }$ und dem Scheitelwinkel $36^{\circ }$ bei $\mathrm {A}$. Es gilt: $\mathrm {\overline {|AC|}} :\mathrm {\overline {|BC|}} =\Phi$.

Vorgehensweise

Es beginnt mit dem Halbieren des Winkels $72^{\circ }$ am Scheitel $\mathrm {B}$. Dabei teilt der generierte Punkt $\mathrm {D}$ die Schenkellänge ${\overline {\mathrm {AC} }}$ im Goldenen Schnitt. Es entsteht dabei das gleichschenklige stumpfwinklige Dreieck $\mathrm {ABD}$ sowie das Dreieck $\mathrm {BCD}$. Dass letzteres auch ein Goldenes Dreieck ist, zeigt die folgende einfache Überprüfung der Winkelweiten.

Am Scheitel $\mathrm {B}$ ergibt sich durch die Winkelhalbierende des Ausgangsdreiecks die Winkelweite $36^{\circ }$; der Basiswinkel am Scheitel $\mathrm {C}$ bleibt unverändert $72^{\circ }$. Wird die Winkelsumme eines ebenen Dreiecks mit $180^{\circ }$ berücksichtigt, ist am Scheitel $\mathrm {D}$ der Basiswinkel ebenfalls $72^{\circ }$. Dies zeigt auf, das entstandene Dreieck $\mathrm {BCD}$ und das Goldene Dreieck $\mathrm {ABC}$ sind zwei zueinander ähnliche Dreiecke.

Für den Nachweis, dass der Punkt $\mathrm {D}$ tatsächlich die Schenkellänge ${\overline {\mathrm {AC} }}$ im Goldenen Schnitt teilt, gilt:

${\overline {\mathrm {AC} }}={\overline {\mathrm {BC} }}\cdot \Phi ={\overline {\mathrm {CD} }}\cdot \Phi ^{2}={\overline {\mathrm {CD} }}\cdot \left(\Phi +1\right)$.

Nun bedarf es noch der Bestimmung des Polpunktes $\mathrm {O}$ als Schnittpunkt der beiden Seitenhalbierenden ${\overline {\mathrm {XC} }}$ und ${\overline {\mathrm {YD} }}$. Die darüber hinaus eingezeichneten goldenen Dreiecke $\mathrm {CDE,DEF,EFG,FGH,GHI}$ und anderes mehr zeigen, dass diese Vorgehensweise beliebig weit fortgesetzt werden kann.

Mit $\mathrm {A,B,C,D}$ und $\mathrm {E}$ sind die ersten fünf Punkte auf der – noch zu konstruierenden – Spirale bestimmt. Hat der Polpunkt $\mathrm {O}$ die Polarkoordinaten $\left(\mathrm {\mu ,\theta } \right)$, so gilt für die Spira mirabilis die Polargleichung

$\mu =\Phi ^{\frac {5}{3\pi }}$.

Angenäherte Spira mirabilis mittels Kreisbögen

• Praktikable Methode als Konstruktion mit Zirkel und Lineal

An den gleichschenkligen stumpfwinkligen Dreiecken wird jeweils um deren Scheitelpunkt mit dem stumpfen Winkel, ein Kreisbogen mit der Winkelweite $108^{\circ }$ (entspricht $180^{\circ }-2\cdot 36^{\circ }$) und dem Radius gleich dem eines Schenkels gezogen.

Mit anderen Worten: Am Dreieck $\mathrm {ABD}$ wird um dessen Scheitelpunkt $\mathrm {D}$ (mit dem stumpfen Winkel), ein Kreisbogen von $\mathrm {A}$ nach $\mathrm {B}$ gezogen. Gleiches gilt für die weiteren ähnlichen Dreiecke.

Geometrisches Mittel

→ Hauptartikel: Geometrisches Mittel

Geometrisches Mittel:
$\mathrm {T}$ teilt die Strecke $\mathrm {\overline {AB}}$ im Verhältnis des Goldenen Schnittes: $x={\sqrt {a(a-x)}};$ $a={\sqrt {x(a+x)}}$

Wird die Strecke $\mathrm {\overline {AB}}$ mit Länge $a$ durch den Punkt $\mathrm {T}$ im Verhältnis des Goldenen Schnitts in zwei Teilstrecken $\mathrm {\overline {AT}}$ und $\mathrm {\overline {BT}}$ mit Längen $x$ und $a-x$ geteilt, so ist $x$ bereits das geometrische Mittel der Zahlen $a$ und $a-x$. Das folgt aus der allgemeinen Definition des geometrischen Mittels ${\bar {x}}_{\text{geom}}={\sqrt[{n}]{x_{1}\cdot x_{2}\dotsm x_{n}}}$, hier: $x={\sqrt[{2}]{a(a-x)}}$. In der Tat folgt mit ${\tfrac {x}{a}}={\tfrac {1}{\Phi }}$ bereits

${\sqrt {a(a-x)}}=a{\sqrt {1-{\frac {1}{\Phi }}}}={\frac {a}{\Phi }}=x$.

Des Weiteren folgt daraus unmittelbar, dass $a$ wiederum das geometrische Mittel von $x$ und $a+x$ ist. Man hat in diesem Fall

${\sqrt {x(a+x)}}=a{\sqrt {{\frac {1}{\Phi }}\left(1+{\frac {1}{\Phi }}\right)}}=a$.

Gefalteter und verknoteter Papierstreifen

Bild 1
Goldener Schnitt im gefalteten und verknoteten Papierstreifen

Bild 2
Symmetrisches Trapez, die gepunkteten Linien zeigen das Fünfeck im Umkreis sowie den Papierstreifen

Mit der im Folgenden beschriebenen Papierstreifen-Methode erzeugt ein sogenannter Überhandknoten ein regelmäßiges Fünfeck (Bild 1), bei dem die Faltenlänge (rot) die Seitenlänge $a$ ist und die Diagonale (grün) – gebildet von der Kante des Papierstreifens – die Länge $\Phi \cdot a$ hat.

Die Diagonale und die sich daran anschließenden drei Seiten des Fünfecks bilden ein symmetrisches Trapez.

Hilfssatz

(1) Ist $\mathrm {ABCD}$ ein symmetrischen Trapez (Bild 2), so gilt

$\mathrm {\overline {AB}} =\mathrm {\overline {BC}} =\mathrm {\overline {CD}}$,

so ist die Diagonale $\mathrm {\overline {AC}}$ auch die Winkelhalbierende des Winkels $\mathrm {BAD}$.

(2) Ist der Winkel $\mathrm {BAD} =72^{\circ }$, so verhält sich

$|\mathrm {\overline {AC}} |:|\mathrm {\overline {AB}} |=\Phi :1$

Beweise

Zu (1)

Vorausgesetzt das Dreieck $\mathrm {BAC}$ ist gleichschenklig, so ist $\angle \mathrm {BAC} =\angle \mathrm {ACB}$ und $\angle \mathrm {CBD} =\angle \mathrm {BDC}$. Aus der Symmetrie des Trapezes ergibt sich die Gleichheit der vier betrachteten Winkel (grün).

Die beiden Diagonalen $\mathrm {\overline {AC}}$ und $\mathrm {\overline {BD}}$ schneiden sich im Scheitel $\mathrm {S}$ und erzeugen damit den Scheitelwinkel $\angle \mathrm {DSA} =\angle \mathrm {BSC}$.

Infolgedessen sind die Basiswinkeln des gleichschenkligen Dreiecks $\mathrm {SDA}$ gleich denen des $\triangle \mathrm {SBC}$. Demzufolge ergibt sich die Gleichheit $\angle \mathrm {BAC} =\angle \mathrm {CBD} =\angle \mathrm {CAD}$. Somit ist bestätigt: $\mathrm {\overline {AC}}$ ist die Winkelhalbierende von $\angle \mathrm {BAD}$.

Zu (2)

Aufgrund der Voraussetzung folgt mittels Hilfssatz (1), der Winkel $\mathrm {CAD} =36^{\circ }$. Wegen der Symmetrie des Trapezes ist auch der Winkel $\mathrm {ADC} =72^{\circ }$. Da die Winkelsumme im Dreieck $\mathrm {ACD} =180^{\circ }$ beträgt, ist auch $\angle \mathrm {DCA} =72^{\circ }$.

Demzufolge ist das Dreieck $\mathrm {ACD}$ wegen seiner Innenwinkeln $36^{\circ },\;72^{\circ },\;72^{\circ }$ ein Goldenes Dreieck. Das Dreieck $\mathrm {ACD}$ hat – für eine mögliche Zahl $a$ – deshalb die Seitenlängen $\Phi \cdot a,\;a,\;\Phi \cdot a$. Somit ist bestätigt:

$|\mathrm {\overline {AC}} |:|\mathrm {\overline {AB}} |=|\mathrm {\overline {AC}} |:|\mathrm {\overline {CD}} |=\Phi :1=\Phi$.

Vorbereitung des Papierstreifens

Bild 3
Papierstreifen mit den vier eingezeichneten Trapezen

Zuerst ist die Streifenbreite gleich der Trapezhöhe zu ermitteln und anschließend die Anordnung der vier Trapeze ($\mathrm {T_{1}\ldots T_{4}}$) darzustellen (Bild 3). Hierzu werden die ermittelten Abmaße des symmetrischen Trapezes $\mathrm {ABCD}$ – z. B. aus einem bereits konstruierten Fünfeck (siehe Bild 2) – auf einem Blatt Papier übertragen. Nach dem Beschriften der beiden Enden mit $\mathrm {E_{1},\;E_{2}}$, bedarf es nur noch des Ausschneidens des Papierstreifens.

Papierfaltung

Bis zum fertigen Fünfeck sind nur drei Faltungen mit gleicher Faltrichtung und das Zusammenziehen des Überhandknotens erforderlich. Begonnen wird mit der Faltlinie $\mathrm {F_{1}}$, demzufolge das Trapez $\mathrm {T_{2}}$ oberhalb des Streifenendes $\mathrm {E_{1}}$ (Bild 4) zum liegen kommt. Der Punkt $\mathrm {A'}$ der Diagonale $\mathrm {\overline {A'C}}$ ist dabei direkt auf dem Punkt $\mathrm {A}$ positioniert. Das regelmäßige Fünfeck $\mathrm {ABCDE}$ kann man bereits jetzt erkennen.

Die zweite Faltung mit der Faltlinie $\mathrm {F_{2}}$ (Bild 5) und dritte Faltung mit $\mathrm {F_{2}}$ (Bild 6) werden analog zur ersten ausgeführt. Schließlich benötigt es nur noch das Durchziehen (Verknoten) des Streifenendes $\mathrm {E_{2}}$ zwischen dem Streifenende $\mathrm {E_{1}}$ und dem Trapez $\mathrm {T_{2}}$, um das gesuchte regelmäßige Fünfeck mit Goldenen Schnitt zu erhalten.

• 
  Bild 4
  Falten der ersten Faltlinie $\mathrm {F_{1}}$
• 
  Bild 5
  Falten der zweiten Faltlinie $\mathrm {F_{2}}$
• 
  Bild 6
  Falten der dritten und letzten Faltlinie $\mathrm {F_{3}}$, Streifenende $\mathrm {E_{2}}$ zwischen dem Streifenende $\mathrm {E_{1}}$ und dem Trapez $\mathrm {T_{2}}$ durchgezogen

Weitere mathematische Eigenschaften

Algebraische Zahlentheorie

Der Goldene Schnitt ist als Nullstelle des Polynoms $X^{2}-X-1$ eine algebraische Zahl. Weil das Polynom normiert ist und alle Koeffizienten ganzzahlig sind, ist der Goldene Schnitt sogar eine algebraisch ganze Zahl. Es sei $K:=\mathbb {Q} (\Phi )=\mathbb {Q} ({\sqrt {5}})$, dann ist $K/\mathbb {Q}$ eine Körpererweiterung von Grad 2. Damit ist $K$ ein quadratischer Zahlkörper. Es ist der reell-quadratische Zahlkörper kleinster Diskriminante, nämlich 5 (der reell-quadratische Zahlkörper mit nächstgrößerer Diskriminante ist $\mathbb {Q} ({\sqrt {2}})$ mit Diskriminante 8). Es sei ${\mathcal {O}}_{K}$ der zugehörige Ganzheitsring. Weil $\Phi$ ganz ist, gilt $\Phi \in {\mathcal {O}}_{K}$, aber mehr als das: Wegen

$N_{K/\mathbb {Q} }(\Phi )=\Phi \Phi '={\frac {1+{\sqrt {5}}}{2}}\cdot {\frac {1-{\sqrt {5}}}{2}}={\frac {1-5}{4}}=-1\in \mathbb {Z} ^{\times }$

ist der Goldene Schnitt sogar Einheit des Ganzheitsrings ${\mathcal {O}}_{K}$. Sein multiplikativ Inverses ist $-\Phi '={\tfrac {{\sqrt {5}}-1}{2}}=\Phi -1$. Dies lässt sich algebraisch allein durch Kenntnis des Minimalpolynoms $X^{2}-X-1$ zeigen:

$\Phi (\Phi -1)=\Phi ^{2}-\Phi =\Phi ^{2}-\Phi -(\Phi ^{2}-\Phi -1)=1$

Jedoch ist der Goldene Schnitt nicht nur eine Einheit des Ganzheitsrings ${\mathcal {O}}_{K}$, sondern sogar Fundamentaleinheit des Ganzheitsrings. Das bedeutet, jedes Element aus ${\mathcal {O}}_{K}^{\times }$ ist von der Form $\pm \Phi ^{n}$ mit $n\in \mathbb {\mathbb {Z} }$. Darüber hinaus bilden $1,\Phi \in {\mathcal {O}}_{K}$ eine $\mathbb {Z}$-Basis von ${\mathcal {O}}_{K}$. Das heißt, jedes Element aus ${\mathcal {O}}_{K}$ lässt sich eindeutig als $a+b\Phi$ mit $a,b\in \mathbb {Z}$ schreiben. Es bildet auch $1,\Phi ^{2}\in {\mathcal {O}}_{K}$ eine $\mathbb {Z}$-Basis von ${\mathcal {O}}_{K}$. Dabei ist $\Phi ^{2}={\tfrac {3+{\sqrt {5}}}{2}}$.

Kettenwurzel

Aus $\Phi ^{2}=1+\Phi$ lässt sich folgende unendliche Kettenwurzel herleiten:

$\Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dotsb }}}}}}}}$

Setzt man also $\Phi _{0}:=1$ und $\Phi _{n}:={\sqrt {1+\Phi _{n-1}}}$ mit $n\geq 1$, so gilt

$\lim _{n\to \infty }\Phi _{n}=\Phi$.

Hinsichtlich der Konvergenzgeschwindigkeit gilt

$\Phi -\Phi _{n}\sim {\frac {2C}{(2\Phi )^{n}}},\qquad n\to \infty$, wobei $C=1{,}0986419643\dots$. Es gilt die exakte Formel

$C=\prod _{n=1}^{\infty }{\frac {2\Phi }{\Phi +\Phi _{n}}}$.

Sie kann auch implizit charakterisiert werden. Es bezeichne $F$ die für $|x|<\Phi ^{2}$ analytische Funktion, so dass die Differentialgleichung

$F(x)=2\Phi F(\Phi -{\sqrt {\Phi ^{2}-x}})$

sowie $F(0)=0$ und $F'(0)=1$ erfüllt ist. Dann gilt $C=\Phi F\left({\tfrac {1}{\Phi }}\right)$.

Trigonometrische und Hyperbolische Funktionen

Aus der Trigonometrie folgt unter anderem

$\Phi =2\cos \left({\frac {\pi }{5}}\right)=2\sin \left({\frac {3\pi }{10}}\right)$

und

${\frac {1}{\Phi }}=2\sin \left({\frac {\pi }{10}}\right)=2\cos \left({\frac {2\pi }{5}}\right)$,

sowie

${\sqrt {3-\Phi }}=2\sin \left({\frac {\pi }{5}}\right)$.

Es ist ${\tfrac {\pi }{5}}$ der volle Spitzwinkel und ${\tfrac {3\pi }{10}}$ die Hälfte des stumpfen Außenwinkels des Pentagramms. Gelegentlich wird die Rolle des Goldenen Schnitts für das Fünfeck als vergleichbar bedeutend bezeichnet wie die der Kreiszahl $\pi$ für den Kreis. Ein weiterer Zusammenhang zur Kreiszahl $\pi$ ergibt sich über den Arkustangens, der Umkehrfunktion des Tangens aus der Trigonometrie. Es gilt

$\pi =2\left(\arctan(\Phi ^{5})+\arctan \left({\frac {1}{\Phi ^{5}}}\right)\right)=6\arctan \left({\frac {1}{\Phi }}\right)-2\arctan \left({\frac {1}{\Phi ^{5}}}\right)$.

Der Goldene Schnitt lässt sich mit Hilfe der Eulerschen Zahl und der hyperbolischen Areasinus-Funktion ausdrücken:

$\Phi ^{\pm 1}=e^{\operatorname {arsinh} \left(\pm {\frac {1}{2}}\right)}$

Unendliche Reihen

Einsetzen von $q={\tfrac {1}{\Phi }}$ in die für $|q|<1$ gültige geometrische Reihenformel $\textstyle \sum _{k=1}^{\infty }q^{k}={\frac {q}{1-q}}$ ergibt:

$\Phi ={\frac {\frac {1}{\Phi }}{1-{\frac {1}{\Phi }}}}=\sum _{k=1}^{\infty }{\frac {1}{\Phi ^{k}}}$.

Es gilt zudem

${\frac {2\log(\Phi )}{\sqrt {5}}}=\left(1-{\frac {1}{2}}-{\frac {1}{3}}+{\frac {1}{4}}\right)+\left({\frac {1}{6}}-{\frac {1}{7}}-{\frac {1}{8}}+{\frac {1}{9}}\right)+\left({\frac {1}{11}}-{\frac {1}{12}}-{\frac {1}{13}}+{\frac {1}{14}}\right)+\cdots$.

Eine weitere Reihe, die den logarithmierten Goldenen Schnitt enthält, beinhaltet die mittleren Binomialkoeffizienten:

$2\log(\Phi )^{2}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n^{2}{\binom {2n}{n}}}}$.

Da gleichzeitig auch die Identität

${\frac {\pi ^{2}}{18}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}$

für die nicht alternierende Variante gilt, wird hier eine „Verbindung“ zwischen der Kreiszahl $\pi$ und dem Goldenen Schnitt gesehen.

Eine schnell konvergente Reihe beinhaltet die Fibonacci-Folge:

$4-\Phi =\sum _{n=0}^{\infty }{\frac {1}{f_{2^{n}}}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}+{\frac {1}{f_{4}}}+{\frac {1}{f_{8}}}+\cdots$.

Rogers-Ramanujan Kettenbrüche

Es gilt

${\frac {e^{-{\frac {2\pi }{5}}}}{{\sqrt {\Phi {\sqrt {5}}}}-\Phi }}=1+{\cfrac {e^{-2\pi }}{1+{\cfrac {e^{-4\pi }}{1+{\cfrac {e^{-6\pi }}{1+\dotsb }}}}}}$,

${\frac {e^{-{\frac {\pi }{5}}}}{{\sqrt {(\Phi -1){\sqrt {5}}}}-(\Phi -1)}}=1-{\cfrac {e^{-\pi }}{1+{\cfrac {e^{-2\pi }}{1-{\cfrac {e^{-3\pi }}{1+\dotsb }}}}}}$.

Dabei bezeichnet $e$ die Eulersche Zahl und $\pi$ die Kreiszahl. Setzt man für $|q|<1$

$R(q):={\frac {q^{\frac {1}{5}}}{1+{\frac {q}{1+{\frac {q^{2}}{1+{\frac {q^{3}}{1+\cdots }}}}}}}}$

so hat man allgemeiner für $\alpha ,\beta >0$ mit $\alpha \beta =\pi ^{2}$

$\left(\Phi +R\left(e^{-2\alpha }\right)\right)\left(\Phi +R\left(e^{-2\beta }\right)\right)={\sqrt {5}}\Phi$,

sowie

$\left(\Phi ^{-1}-R\left(-e^{-\alpha }\right)\right)\left(\Phi ^{-1}-R\left(-e^{-\beta }\right)\right)={\sqrt {5}}\Phi ^{-1}$.

Diese Entdeckungen gehen auf Srinivasa Ramanujan zurück. Die Funktion $R$ wird auch als Rogers-Ramanujan-Kettenbruch bezeichnet und hat Verbindungen zur Theorie der Modulformen.

Zusammenhang zur Chintschin-Levy-Konstante

Definiert man den nächstgelegenen ganzzahligen Kettenbruch (englisch: nearest integer continued fraction) für reelle Zahlen $-{\tfrac {1}{2}}<x<{\tfrac {1}{2}}$ via

$x=1+{\frac {1}{c_{1}+{\frac {1}{c_{2}+\cdots }}}}$

über die Rekursion

$c_{1}=\left\lfloor {\frac {1}{x}}+{\frac {1}{2}}\right\rfloor ,\quad x_{1}={\frac {1}{x}}-c_{2},\quad c_{2}=\left\lfloor {\frac {1}{x_{1}}}+{\frac {1}{2}}\right\rfloor ,\quad x_{2}={\frac {1}{x_{1}}}-c_{2},\ldots$

so können die $c_{j}$ eventuell negative Zahlen sein. Für die Chintschin-Levy-Konstante gilt in diesem Falle

$\lim _{n\to \infty }{\sqrt[{n}]{|c_{1}\cdots c_{n}|}}=\left({\frac {5\Phi +3}{5\Phi +2}}\right)^{\frac {\log(2)}{\log(\Phi )}}\prod _{k=1}^{\infty }\left({\frac {8(k-1)\Phi +(2k-3)^{2}+4}{8(k-1)\Phi +(2k-3)^{2}}}\right)^{\frac {\log(k)}{\log(\Phi )}}=5{,}4545172445\ldots$

für alle betroffenen reellen Zahlen bis auf eine Lebesgue-Nullmenge. Das bedeutet, dass alle Zahlen $-{\tfrac {1}{2}}<x<{\tfrac {1}{2}}$, „bis auf 0 %“ in einem asymptotischen Sinne, diese Gesetzmäßigkeit erfüllen. Ist zudem ${\tfrac {P_{n}}{Q_{n}}}$ der (vollständig gekürzte) $n$-te Näherungsbruch dieser Konstruktion, so gilt wieder bis auf Nullmenge

$\lim _{n\to \infty }{\sqrt[{n}]{|Q_{n}|}}=e^{\frac {\pi ^{2}}{12\log(\Phi )}}=5{,}5243079702\ldots$.

Alternierende Bit-Mengen

Jede natürliche Zahl lässt sich eindeutig über das Binärsystem durch Nullen und Einsen ausdrücken. Innerhalb einer solchen Darstellung lassen sich nun sog. alternierende Bit-Mengen abzählen, die wie folgt erklärt sind:

• Von links nach rechts wechseln sich in den ausgewählten Positionen die Zahlen 1 und 0 ab.
• Die Zahl ganz zur Linken der ausgewählten Positionen ist 1.
• Die Zahl ganz zur Rechten der ausgewählten Positionen ist 0.

Man bezeichnet die Anzahl der alternierenden Bit-Mengen einer Zahl $n$ mit $c(n)$. Es ist zum Beispiel $c(26)=8$, denn im Binärsystem gilt $26=11010$, und daher sind die möglichen alternierenden Bit-Mengen (aus formalen Gründen inklusive der leeren Menge):

$\{\},\{5,3\},\{5,1\},\{4,3\},\{4,1\},\{2,1\},\{5,3,2,1\},\{4,3,2,1\}$.

Es bezieht sich z. B. $\{5,3,2,1\}$ auf ${\color {red}{1}}1{\color {red}{010}}$. Es entspricht $c(n)$ gleichzeitig der Anzahl der Möglichkeiten, $n$ als Summe von Zweierpotenzen zu schreiben, ohne dabei eine Potenz mehr als zweimal zu benutzen. Diese zahlentheoretische Funktion $c$ hat eine Verbindung zum Goldenen Schnitt, denn es konnte

$0{,}9588<\limsup _{n\to \infty }{\frac {c(n)}{n^{\frac {\log(\Phi )}{\log(2)}}}}<1{,}1709$

gezeigt werden. Dabei ist $\limsup$ der Limes superior. Ob der innere Wert sogar 1 beträgt, konnte bisher nicht gezeigt werden.

Verbindung zu speziellen Funktionen

Über die Formel

$\Gamma \left({\frac {1}{5}}\right)\Gamma \left({\frac {4}{5}}\right)={\frac {2}{5}}\pi {\sqrt {5}}{\sqrt {2+\Phi }}$

wird eine direkte Verbindung zur Gammafunktion hergestellt. Dabei ist wie üblich $\pi$ die Kreiszahl. Die Gammafunktion stellt eine Fortsetzung der Fakultätsfunktion auf komplexe Zahlen dar.

Für den Trilogarithmus $\mathrm {Li} _{3}$ gilt die Identität

$\mathrm {Li} _{3}(2-\Phi )={\frac {4}{5}}\zeta (3)+{\frac {\pi ^{2}}{15}}\log(2-\Phi )-{\frac {1}{12}}\log(2-\Phi )^{3}$.

Dabei bezeichnet $\zeta (3)$ den Wert der Riemannschen Zeta-Funktion an der Stelle $3$, der auch unter Apéry-Konstante bekannt ist.

Varianten und Verallgemeinerungen

Silberner Schnitt

→ Hauptartikel: Silberner Schnitt

Silberner Schnitt im regelmäßigen Achteck, Größenverhältnisse der Streckenteile:
$\delta ={\frac {2a+b}{a}}={\frac {a}{b}}$

Der Silberne Schnitt beschreibt das definierte Größenverhältnis zweier Abschnitte mit unterschiedlicher Größe (oder Länge) einer Strecke (oder eines Bereichs).

Ist etwas „nach dem Silbernen Schnitt geteilt“, so versteht man darunter:

Das Verhältnis der Summe des verdoppelten größeren und des kleineren Teils zum größeren Teil ist gleich dem Verhältnis des größeren zum kleineren Teil.

Es gilt also:

${\frac {2a+b}{a}}={\frac {a}{b}}$.

Er hat den Wert

$\delta =1+{\sqrt {2}}=2,414\ldots$

Ebenso wie der Goldene Schnitt ist er also eine quadratisch-irrationale Zahl. Wegen $\delta =2+{\tfrac {1}{\delta }}$ gilt

$\delta =2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\dotsb }}}}}}$.

Variante über Rechteckflächen

Es soll eine gegebene Strecke $\mathrm {\overline {AB}}$ mit der Länge $a$ um eine Länge $x$ verlängert werden, sodass ein Rechteck mit der Verlängerung $x$ als Breite und $a+x$ als Länge, gleich ist, einem vorab bestimmten Rechteck mit der Länge $m$ und der Breite $n$. Es soll also

$x\left(x+a\right)=mn$

gelten, was sich auf die quadratische Gleichung $x^{2}+ax-mn=0$ reduziert. Daraus ergibt sich über die Mitternachtsformel sogleich

$x=-{\frac {a}{2}}+{\sqrt {{\frac {a^{2}}{4}}+mn}}$

da $x>0$ gelten soll. Ergeben Konstruktion oder Abmessungen des vorab bestimmten Rechtecks speziell

$mn=a^{2}$

so ergibt sich zusätzlich

$x\left(x+a\right)=a^{2}\Rightarrow {\frac {x}{a}}={\frac {a}{a+x}}$

nach dem Umformen erhält man mit

${\frac {a-x}{x}}={\frac {x}{a}}$

das Teilungsverhältnis des Goldene Schnittes. Die Verlängerung $x$ ist in diesem Falle die mittlere Proportionale, sprich das geometrische Mittel, zwischen $a-x$ und $a$.

Ephraim Salomon Unger zeigt seinen Weg, der zur Verlängerung $x$ führt:

„Man findet also die gesuchte Verlängerung, wenn man die mittlere Proportionale zwischen $m$ und $n$ als die eine Kathete und ${\tfrac {a}{2}}$ als die andere Kathete eines rechtwinkligen Dreiecks annimmt; und von der Hypotenuse desselben ${\tfrac {1}{2}}$ $a$ abschneidet.“

– Ephraim Salomon Unger: Praktische Übungen für angehende Mathematiker

Die beiden Rechtecke $\mathrm {AMOP}$ (blau) und $\mathrm {AGFE}$ (grün) haben den gleichen Flächeninhalt. Der Punkt $\mathrm {B}$ teilt $|\mathrm {\overline {AM}} |$ im Goldenen Schnitt, sofern $mn=a^{2}$ gilt.

Konstruktion

(Die Konstruktion wurde, wegen nicht einsehbarer Skizze, der obigen Beschreibung von Unger nachempfunden.)

Es beginnt mit der Halbgeraden $\mathrm {g}$ und dem Abtragen der gegebenen Strecke $\mathrm {\overline {AB}}$ mit Länge $a$ auf $\mathrm {g}$. Der Punkt $\mathrm {E}$, für die Länge $m$ des (grünen) Rechtecks, wird rechts von $\mathrm {B}$ beliebig auf $\mathrm {g}$ gesetzt. Im allgemeinen Fall darf die Breite $n$ frei gewählt werden.

Soll hingegen zum Schluss der Punkt $\mathrm {B}$ die gesuchte Strecke $\mathrm {\overline {AM}}$ mit Länge $a+x$ im Goldenen Schnitt teilen, muss $n$ aus $m$ erst noch bestimmt werden. Hierfür wird die Breite $n$ des Rechtecks mittels des Quadrats $\mathrm {ADCB}$ mit Fläche $a^{2}$ durch die Verbindung der Punkte $\mathrm {D}$ mit $\mathrm {E}$ und deren Parallele $\mathrm {\overline {CF}}$ festgelegt. Es folgt das Einzeichnen des Rechtecks $\mathrm {AGFE}$, dessen Flächeninhalt mit $mn=a^{2}$ gleich dem des Quadrates $\mathrm {ADCB}$ ist. Diese Vorgehensweise ist in der nebenstehenden Skizze dargestellt. Falls keine stetige Teilung erzielt werden soll, wird dieser erste Schritt weggelassen.

Es folgt der Kreisbogen mit Radius $n$ um $\mathrm {E}$ bis er die Halbgerade $\mathrm {g}$ in $\mathrm {H}$ schneidet. Nach dem Bestimmen des Mittelpunktes $\mathrm {I}$ der Strecke $\mathrm {\overline {AH}}$ und dem Ziehen des Kreisbogens mit Radius $\mathrm {|{\overline {IH}}|}$ um $\mathrm {I}$, wird die Senkrechte zu $\mathrm {\overline {AH}}$ in $\mathrm {E}$ errichtet, bis sie den Kreisbogen in $\mathrm {J}$ schneidet. Die Strecke $\mathrm {\overline {EJ}}$ entspricht dem geometrischen Mittel der Längen $m$ und $n$. Nach dem Halbieren der Strecke $\mathrm {\overline {AB}}$ in $\mathrm {K}$ wird $\mathrm {\overline {AK}}$ mit Länge ${\tfrac {a}{2}}$ ab $\mathrm {E}$ auf die Halbgerade $\mathrm {g}$ übertragen und der so erzeugte Schnittpunkt $\mathrm {L}$ mit $\mathrm {J}$ verbunden. Daraus ergibt sich das rechtwinklige Dreieck $\mathrm {ELJ}$. Der sich anschließende Kreisbogen mit Radius ${\tfrac {a}{2}}$ um $\mathrm {J}$ liefert mit $\mathrm {\overline {LN}}$ die gesuchte Länge $x$. Die Übertragung der Länge $x$ auf $\mathrm {g}$ ab $\mathrm {B}$ erzeugt die Gesamtstrecke $\mathrm {\overline {AM}}$ mit Länge $a+x$.

Der Punkt $\mathrm {B}$ teilt somit die Streckenlänge $|\mathrm {\overline {AM}} |$ im Goldenen Schnitt, sofern $mn=a^{2}$ gilt.

Das abschließend errichtete blaue Rechteck $\mathrm {AMOP}$ über $\mathrm {\overline {AM}}$ mit der Breite $x$ hat ganz allgemein den gleichen Flächeninhalt wie das grüne Rechteck $\mathrm {AGFE}$.

Kubische Varianten

Man definiert die Perrin-Folge rekursiv durch $g_{0}:=3$, $g_{1}:=0$, $g_{2}:=2$, und $g_{n}=g_{n-2}+g_{n-3}$ für alle $\geq 3$. Ähnlich wie sich die Quotienten nacheinander folgender Fibonacci-Zahlen dem Goldenen Schnitt nähern, folgt für die Perrin-Zahlen

$\lim _{\to \infty }{\frac {g_{n+1}}{g_{n}}}=\psi$

wobei $\psi >0$ die charakteristische Gleichung $\psi ^{3}-\psi -1=0$ erfüllt. Durch Radikale ausgedrückt ergibt sich

$\psi ={\sqrt[{3}]{{\tfrac {1}{2}}+{\tfrac {\sqrt {69}}{18}}}}+{\frac {1}{3{\sqrt[{3}]{{\tfrac {1}{2}}+{\tfrac {\sqrt {69}}{18}}}}}}=1{,}3247\ldots$

Ähnlich wie beim Goldenen Schnitt besitzt auch $\psi$ eine Entwicklung als Kettenwurzel, dieses Mal jedoch kubisch:

$\psi ={\sqrt[{3}]{1+{\sqrt[{3}]{1+{\sqrt[{3}]{1+\cdots }}}}}}$.

In Anlehnung an Goldene Konstante wird $\psi$ gelegentlich auch als „Plastik-Konstante“ bezeichnet.

Im Falle der „Tribonacci-Folge“ $h_{0}=h_{1}:=0$, $h_{2}:=1$ und $h_{n}:=h_{n-1}+h_{n-2}+h_{n-2}$ für $n\geq 3$ gilt

$\lim _{n\to \infty }{\frac {h_{n+1}}{h_{n}}}=\chi ={\sqrt[{3}]{{\tfrac {19}{27}}+{\tfrac {\sqrt {33}}{9}}}}+{\frac {4}{9{\sqrt[{3}]{{\tfrac {19}{27}}+{\tfrac {\sqrt {33}}{9}}}}}}=1{,}8392\ldots$.

Es erfüllt $\chi$ die Gleichung $\chi ^{3}-\chi ^{2}-\chi -1=0$.

Verallgemeinerte Kettenbrüche

Das Konzept der Kettenbruchentwicklung lässt sch für ganze positive Zahlen $p,q$ verallgemeinern durch

$w(p,q):=q+{\frac {p+{\frac {1}{q+{\frac {p+\cdots }{q+\cdots }}}}}{q+{\frac {p+{\frac {1+\cdots }{q+\cdots }}}{q+{\frac {p+\cdots }{q+\cdots }}}}}}$.

Dies entspricht einer fraktalen Konstruktion durch die iterative Anwendung der Ersetzungsregeln

$p\mapsto p+{\frac {1}{q}},\qquad q\mapsto q+{\frac {p}{q}}$.

Dieser verallgemeinerte Kettenbruch konvergiert stets gegen die positive Lösung der Gleichung

$x^{3}-qx^{2}-px-1=0$.

Setzt man in diesem Beispiel also insbesondere $p=q=1$, so ergibt sich als Grenzwert die Zahl $\chi$, die eine kubische Verallgemeinerung des Goldenen Schnittes darstellt.

Asymptotik zufälliger Fibonacci-Folgen

Setzt man $x_{0}=x_{1}:=1$, sowie

$x_{n}=\pm \ x_{n-1}\pm x_{n-2}$

für $n\geq 2$, wobei die Vorzeichen durch unabhängige Zufallsvariablen mit gleichen Wahrscheinlichkeiten für $\pm 1$ gegeben sind, zeigte D. Viswanadt

$\lim _{n\to \infty }{\sqrt[{n}]{|x_{n}|}}=1{,}13198824\ldots$

mit Wahrscheinlichkeit 1. Die gewöhnliche Fibonacci-Folge, die sich in dieser Art Limes dem Goldenen Schnitt annähert, entspricht dem Extremfall, dass die Zufallsgrößen stets den Wert $+1$ annehmen, was aber mit einer (asymptotischen) Wahrscheinlichkeit von 0 Prozent eintritt.

Vorkommen in der Natur

Biologie

Blattstand einer Pflanze mit einem Blattabstand nach dem Goldenen Winkel

Das spektakulärste Beispiel für Verhältnisse des Goldenen Schnittes in der Natur findet sich bei der Anordnung von Blättern (Phyllotaxis) und in Blütenständen mancher Pflanzen. Bei diesen Pflanzen teilt der Winkel – wie im Bild vereinfacht dargestellt – zwischen zwei aufeinanderfolgenden Blättern den Vollkreis von 360° im Verhältnis des Goldenen Schnittes, wenn die beiden Blattansätze durch eine Parallelverschiebung eines der Blätter entlang der Pflanzenachse zur Deckung gebracht werden. Es handelt sich um den Goldenen Winkel von etwa 137,5°.

Die daraus entstehenden Strukturen werden auch als selbstähnlich bezeichnet: Auf diese Weise findet sich ein Muster einer tieferen Strukturebene in höheren Ebenen wieder. Beispiele sind die Sonnenblume, Kohlarten, Kiefernnadeln an jungen Ästen, Zapfen, Agaven, viele Palmen- und Yuccaarten sowie die Blütenblätter der Rose, um nur einige zu nennen.

Ursache ist das Bestreben dieser Pflanzen, ihre Blätter auf Abstand zu halten. Es wird vermutet, dass sie dazu an jedem Blattansatz einen besonderen Wachstumshemmer (Inhibitor) erzeugen, der im Pflanzenstamm – vor allem nach oben, in geringerem Umfang in seitlicher Richtung – diffundiert. Dabei bilden sich in verschiedene Richtungen bestimmte Konzentrationsgefälle aus. Das nächste Blatt entwickelt sich an einer Stelle des Umfangs, wo die Konzentration minimal ist. Dabei stellt sich ein bestimmter Winkel zum Vorgänger ein. Würde dieser Winkel den Vollkreis im Verhältnis einer rationalen Zahl ${\tfrac {m}{n}}$ teilen, dann würde dieses Blatt genau in die gleiche Richtung wachsen wie dasjenige $n$ Blätter zuvor. Der Beitrag dieses Blattes zur Konzentration des Inhibitors ist aber an dieser Stelle gerade maximal. Daher stellt sich ein Winkel mit einem Verhältnis ein, das alle rationalen Zahlen meidet. Die Zahl ist nun aber gerade die Goldene Zahl (siehe oben). Da bisher kein solcher Inhibitor isoliert werden konnte, werden auch andere Hypothesen diskutiert, wie die Steuerung dieser Vorgänge in analoger Weise durch Konzentrationsverteilungen von Nährstoffen.

Der Nutzen für die Pflanze könnte darin bestehen, dass auf diese Weise von oben einfallendes Sonnenlicht (bzw. Wasser und Luft) optimal genutzt wird, eine Vermutung, die bereits Leonardo da Vinci äußerte, oder im effizienteren Transport der durch Photosynthese entstandenen Kohlenhydrate im Phloemteil der Leitbündel nach unten. Die Wurzeln von Pflanzen weisen den Goldenen Winkel weniger deutlich auf. Bei anderen Pflanzen wiederum treten Blattspiralen mit anderen Stellungswinkeln zutage. So wird bei manchen Kakteenarten ein Winkel von 99,5° beobachtet, der mit der Variante der Fibonacci-Folge 1, 3, 4, 7, 11, … korrespondiert. In Computersimulationen des Pflanzenwachstums lassen sich diese verschiedenen Verhaltensweisen durch geeignete Wahl der Diffusionskoeffizienten des Inhibitors provozieren.

Fichtenzapfen mit 5, 8 und 13 Fibonacci-Spiralen

Bei vielen nach dem Goldenen Schnitt organisierten Pflanzen bilden sich in diesem Zusammenhang so genannte Fibonacci-Spiralen aus. Spiralen dieser Art sind besonders gut zu erkennen, wenn der Blattabstand im Vergleich zum Umfang der Pflanzenachse besonders klein ist. Sie werden nicht von aufeinanderfolgenden Blättern gebildet, sondern von solchen im Abstand $n$, wobei $n$ eine Fibonacci-Zahl ist. Solche Blätter befinden sich in enger Nachbarschaft, denn das $n$-Fache des Goldenen Winkels $2\pi -{\tfrac {2\pi }{\Phi }}\approx 137{,}5^{\circ }$ ist ungefähr ein Vielfaches von 360° wegen

$n\cdot 360^{\circ }\cdot \left(1-{\frac {1}{\Phi }}\right)\approx n\cdot \left(1-{\frac {m}{n}}\right)\cdot 360^{\circ }=(n-m)\cdot 360^{\circ }=k\cdot 360^{\circ }$,

wobei $m$ die nächstkleinere Fibonacci-Zahl zu $n$ und $k$ die nächstkleinere Fibonacci-Zahl zu $m$ ist. Da jedes der Blätter zwischen diesen beiden zu einer anderen Spirale gehört, sind $n$ Spiralen zu sehen. Ist ${\tfrac {n}{m}}$ größer als $\Phi$, so ist das Verhältnis der beiden nächsten Fibonacci-Zahlen kleiner und umgekehrt. Daher sind in beide Richtungen Spiralen zu aufeinander folgenden Fibonaccizahlen zu sehen. Der Drehsinn der beiden Spiralentypen ist dem Zufall überlassen, sodass beide Möglichkeiten gleich häufig auftreten.

Berechneter Blütenstand mit 1000 Früchten im Goldenen Winkel – Es stellen sich 13, 21, 34 und 55 Fibonacci-Spiralen ein.

Sonnenblume mit 34 und 55 Fibonacci-Spiralen

Besonders beeindruckend sind Fibonacci-Spiralen (die damit wiederum dem Goldenen Schnitt zugeordnet sind) in Blütenständen, wie bei Sonnenblumen. Dort sitzen Blüten, aus denen später Früchte entstehen, auf der stark gestauchten, scheibenförmigen Blütenstandsachse dicht nebeneinander, wobei jede einzelne Blüte einem eigenen Kreis um den Mittelpunkt des Blütenstandes zugeordnet werden kann. Wachstumstechnisch aufeinander folgende Früchte liegen daher räumlich weit auseinander, während direkte Nachbarn wieder einen Abstand entsprechend einer Fibonacci-Zahl haben. Im äußeren Bereich von Sonnenblumen werden 34 und 55 Spiralen gezählt, bei größeren Exemplaren 55 und 89 oder sogar 89 und 144. Die Abweichung vom mathematischen Goldenen Winkel, die in diesem Fall nicht überschritten wird, beträgt weniger als 0,01 %.

Der Goldene Schnitt ist außerdem in radiärsymmetrischen fünfzähligen Blüten erkennbar wie bei der Glockenblume, der Akelei und der (wilden) Hecken-Rose. Der Abstand der Spitzen von Blütenblättern nächster Nachbarn zu dem der übernächsten steht wie beim regelmäßigen Fünfeck üblich in seinem Verhältnis. Das betrifft ebenso Seesterne und andere Tiere mit fünfzähliger Symmetrie.

Goldener Schnitt im Efeublatt

Darüber hinaus wird der Goldene Schnitt im Verhältnis der Längen aufeinander folgender Stängelabschnitte mancher Pflanzen vermutet wie bei der Pappel. Im Efeublatt stehen die Blattachsen a und b (siehe Abbildung) ungefähr im Verhältnis des Goldenen Schnittes. Diese Beispiele sind jedoch umstritten.

Noch im 19. Jahrhundert war die Ansicht weit verbreitet, dass der Goldene Schnitt ein göttliches Naturgesetz sei und in vielfacher Weise in den Proportionen des menschlichen Körpers realisiert wäre. So nahm Adolf Zeising in seinem Buch über die Proportionen des menschlichen Körpers an, dass der Nabel die Körpergröße im Verhältnis des Goldenen Schnittes teile, und der untere Abschnitt werde durch das Knie wiederum so geteilt. Ferner scheinen die Verhältnisse benachbarter Teile der Gliedmaßen wie bei Ober- und Unterarm sowie bei den Fingerknochen ungefähr in diesem Verhältnis zu stehen. Eine genaue Überprüfung ergibt jedoch Streuungen der Verhältnisse im 20-%-Bereich. Oft enthält auch die Definition, wie die Länge eines Körperteils exakt zu bestimmen sei, eine gewisse Portion Willkür. Ferner fehlt dieser These eine wissenschaftliche Grundlage. Es dominiert daher weitgehend die Ansicht, dass diese Beobachtungen lediglich die Folge gezielter Selektion von benachbarten Paaren aus einer Menge von beliebigen Größen sind.

Bahnresonanzen

Seit langem ist bekannt, dass die Umlaufzeiten mancher Planeten und Monde in Verhältnis kleiner ganzer Zahlen stehen wie Jupiter und Saturn mit $2:5$ oder die Jupitermonde Io, Ganymed und Europa mit $1:2:4$. Derartige Bahnresonanzen stabilisieren die Bahnen der Himmelskörper langfristig gegen kleinere Störungen. Erst 1964 wurde entdeckt, dass noble Verhältnisse, wie sie im Fall $1:\Phi$ vorliegen würden, stabilisierend wirken können. Derartige Bahnen werden KAM-Bahnen genannt, wobei die drei Buchstaben für die Namen der Entdecker Andrei Kolmogorow, V. I. Arnold und Jürgen Moser stehen.

Die Cassini-Teilungen in den Saturnringen zeigen, was passiert, wenn statt nobler Zahlen einfache rationale Zahlen vorherrschen: Die Gesteins- und Eisteilchen, aus denen die Ringe bestehen und deren Umlaufperioden in einem einfachen rationalen Verhältnis zu den Perioden der Saturnmonde stehen, werden durch die Resonanzeffekte zwischen den entsprechenden Umlaufperioden einfach aus ihrer Bahn geworfen. In der Tat hängt die Stabilität des Sonnensystems davon ab, dass zumindest einige der Bahnperiodenverhältnisse nobel sind.

Schwarze Löcher

Kontrahierbare kosmische Objekte ohne feste Oberfläche, wie Schwarze Löcher oder die Sonne, haben aufgrund ihrer Eigengravitation die paradoxe Eigenschaft, heißer zu werden, wenn sie Wärme abstrahlen (negative Wärmekapazität). Bei rotierenden Schwarzen Löchern findet ab einem kritischen Drehimpuls ein Umschlag von negativer zu positiver Wärmekapazität statt, wobei dieser Tipping-Point von der Masse des Schwarzen Loches abhängt. In einer $d$-dimensionalen Raumzeit kommt dabei eine Metrik ${\bigl (}{\begin{smallmatrix}d-3&1\\1&0\end{smallmatrix}}{\bigr )}$ ins Spiel, deren Eigenwerte $\Phi$ für $d=4$ sich als Nullstellen des charakteristischen Polynoms

$\left|{\begin{pmatrix}1-\Phi &1\\1&-\Phi \end{pmatrix}}\right|=\Phi ^{2}-\Phi -1$

ergeben.

Kristallstrukturen

Quasikristalle

Der Goldene Schnitt tritt bei den Quasikristallen der Festkörperphysik in Erscheinung, die 1984 von Dan Shechtman und seinen Kollegen entdeckt wurden. Dabei handelt es sich um Strukturen mit fünfzähliger Symmetrie, aus denen sich aber, wie bereits Kepler erkannte, keine streng periodischen Kristallgitter aufbauen lassen, wie dies bei Kristallen üblich ist. Entsprechend groß war die Überraschung, als bei Röntgenstrukturanalysen Beugungsbilder mit fünfzähliger Symmetrie gefunden wurden. Diese Quasikristalle bestehen strukturell aus zwei verschiedenen rhomboedrischen Grundbausteinen, mit denen der Raum zwar lückenlos, jedoch ohne globale Periodizität gefüllt werden kann (Penrose-Parkettierung). Beide Rhomboeder setzten sich aus den gleichen rautenförmigen Seitenflächen zusammen, die jedoch unterschiedlich orientiert sind. Die Form dieser Rauten lässt sich nun dadurch definieren, dass ihre Diagonalen im Verhältnis des Goldenen Schnittes stehen. Für die Entdeckung von Quasikristallen wurde Shechtman 2011 der Nobelpreis für Chemie verliehen.

Kobalt-Niobat

Im atomaren Aufbau des Kristalls aus Kobalt-Niobat entdeckten Forscher des Helmholtz-Zentrums Berlin für Materialien und Energie (HZB) Symmetrieeigenschaften erstmal in fester Materie, die auch den Goldenen Schnitt kennzeichnen (veröffentlicht in der Zeitschrift Science, Januar 2010). Für Untersuchungen der Quanteneigenschaften, sprich Verhalten atomarer Teilchen in der Quantenwelt nach Heisenbergs Unschärferelation, findet Kobalt-Niobat Verwendung. Ausschlaggebend dafür sind insbesondere, die auf besondere Weise angeordneten atomaren Bestandteile sowie die magnetischen Eigenschaften des Kristalls. Dies bedeutet, hervorgerufen durch den im Elektron vorhandenen Eigenimpuls (Spin), bilden in diesem Kristall die aneinandergereihten Atome eine sogenannte Spinkette mit der Wirkung eines dünnen Stabmagnets. Wirkt nun ein Magnetfeld rechtwinklig auf die Spinkette, geht sie in einen neuen Zustand über. Physiker stellen sich diesen Zustand als fraktales Muster vor.

Als die Forscher dies als Modell für die Untersuchung des Festkörpermagnetismus nutzten, machten sie eine überraschende Entdeckung: Die Wechselwirkung, die benachbarte Spinketten miteinander eingehen, entspricht der Schwingung einer Gitarrensaite, deren ersten beiden Resonanzfrequenzen im Verhältnis $1{,}618\ldots$, zueinander stehen. „Was genau dem Goldenen Schnitt entspricht“, so Radu Coldea, Leiter des über zehn Jahre laufenden internationalen Projektes.

Vergleich mit anderen prominenten Seitenverhältnissen

Die folgende Abbildung zeigt im Vergleich verschiedene Rechtecke mit prominenten Seitenverhältnissen in der Umgebung von $\Phi =1{,}618\ldots$ Angegeben ist jeweils das Verhältnis von Höhe zu Breite und der entsprechende Zahlenfaktor:

• ${\text{4 : 3}}$ – Traditionelles Fernsehformat und Ballenformat für Packpapier. Auch bei älteren Computermonitoren verwendet (z. B.: 1024 × 768 Pixel). Dieses Format geht zurück auf Thomas Alva Edison, der 1889 das Format des klassischen Filmbildes (35-mm-Film) auf 24 mm × 18 mm festlegte.
• $\textstyle {\sqrt {2}}\ :1$ – Das Seitenverhältnis beim DIN-A4-Blatt und verwandten DIN-/EN-/ISO-Maßen. Bei einer Halbierung durch einen Schnitt, der die längeren Seiten des Rechtecks halbiert, entstehen wiederum Rechtecke mit demselben Seitenverhältnis.
• ${\text{3 : 2}}$ – Seitenverhältnis beim Kleinbildfilm (36 mm × 24 mm).
• ${\text{16 : 10}}$ – Manche Computerbildschirme (1920 × 1200 Pixel). Diese passen mit 1,6 : 1 fast zum Goldenen Schnitt.
• ${\boldsymbol {\textstyle \Phi \ :1}}$ – Seitenverhältnis im Goldenen Schnitt. Im Bild approximiert mit 144 × 89 Pixel (theoretischer Fehler nur 5 · 10⁻⁵). Die beiden benachbarten Rechtecke 3:2 und 5:3 haben – wie auch das dargestellte Rechteck mit 144:89 – Seitenverhältnisse von aufeinanderfolgenden Fibonacci-Zahlen und approximieren daher ebenfalls den Goldenen Schnitt vergleichsweise gut.
• ${\text{5 : 3}}$ – Findet neben vielen anderen als Kinofilmformat Verwendung.
• ${\text{16 : 9}}$ – Breitbildfernsehen.

Anwendung in Technik und Mathematik

Der Goldene Zirkel (Reduktionszirkel)

→ Hauptartikel: Reduktionszirkel

Anstatt stets neu konstruieren zu müssen, wurde im 19. Jahrhundert von Künstlern und Handwerkern ein Goldener Zirkel – ein auf das Goldene Verhältnis eingestellter Reduktionszirkel – benutzt. Insbesondere im Schreinerhandwerk kam ein ähnliches Instrument in Form eines Storchschnabels zur Anwendung. Bereits in der Antike fand der Reduktionszirkel Verwendung, dies zeigt z. B. der Fund eines Vorläufers bei den Ausgrabungen in Pompeji. Solche Zirkel, wie die im Folgenden näher beschriebenen Beispiele, werden auch heute noch hergestellt. Die einfachste Ausführung besteht nur aus zwei Stäben – in moderner Bauweise zusätzlich mit vier Nadeln – deren Drehpunkt sie im Goldenen Schnitt teilt.

Für die Lage des Drehpunktes gilt:

$|{\overline {\mathrm {AE} }}|:|{\overline {\mathrm {CE} }}|=|{\overline {\mathrm {AC} }}|:|{\overline {\mathrm {AE} }}|=\Phi$.

• 
  Lage des Drehpunktes
• 
  Innere Teilung
• 
  Äußere Teilung

Mithilfe eines solchen Reduktionszirkels gelingt die Teilung einer gegebenen Streckenlänge ${|{\overline {\mathrm {AB} }}|}$ in $C$ (innere Teilung) sowie die Verlängerung einer Strecke ${|{\overline {\mathrm {AB} }}|}$ um die Länge $b$ (äußere Teilung). Punkt $B$ teilt die Streckenlänge ${|{\overline {\mathrm {AC} }}|}$ im Goldenen Schnitt.

Der von Adalbert Göringer im Jahre 1893 erfundene Reduktions- bzw. Proportionalzirkel – dargestellt in den nebenstehenden Bildern – ist eine Weiterentwicklung. Um als Werkzeug für die innere und äußere Teilung dienen zu können, müssen die Bauteile des Reduktionszirkels ebenfalls die Teilung nach dem Goldenen Schnitt beinhalten.

Wenn

$|{\overline {\mathrm {AE} }}|:|{\overline {\mathrm {DE} }}|=|{\overline {\mathrm {AD} }}|:|{\overline {\mathrm {AE} }}|=|{\overline {\mathrm {BG} }}|:|{\overline {\mathrm {DG} }}|=|{\overline {\mathrm {BD} }}|:|{\overline {\mathrm {BG} }}|=|{\overline {\mathrm {FG} }}|:|{\overline {\mathrm {CF} }}|=|{\overline {\mathrm {CG} }}|:|{\overline {\mathrm {FG} }}|$,

dann gilt:

$|{\overline {\mathrm {BC} }}|:|{\overline {\mathrm {AC} }}|=|{\overline {\mathrm {AB} }}|:|{\overline {\mathrm {BC} }}|=\Phi$.

Rechteck mit einbeschriebenem Dreieck

Goldener Schnitt im Rechteck mit einbeschriebenem Dreieck

„Man beschreibe in ein gegebenes Rechteck ein Dreieck (das mit dem Rechteck eine Ecke gemeinsam hat) so ein, daß die drei dabei entstehenden Dreiecke die gleiche Fläche haben.“

– A. Beutelspacher, B. Petri: Der Goldene Schnitt

Die Flächengleichheit bedeutet, dass ${\frac {a(c+d)}{2}}={\frac {bd}{2}}={\frac {c(a+b)}{2}}$ gilt.

Aus der Gleichheit des ersten und zweiten Terms folgt $a={\frac {bd}{c+d}}$ (1) und aus der Gleichheit des ersten und dritten Terms $a={\frac {bc}{d}}$ (2).

Aus (1) und (2) ergibt sich:

$d^{2}=c(c+d)\Leftrightarrow \left({\frac {d}{c}}\right)^{2}-\left({\frac {d}{c}}\right)-1=0\Leftrightarrow {\frac {d}{c}}=\Phi$.

Wegen

$a={\frac {bc}{d}}\Leftrightarrow {\frac {b}{a}}={\frac {d}{c}}$

gilt dann auch:

${\frac {b}{a}}=\Phi$

Gleichschenkliges Dreieck, gegebene Strecke teilt gesuchten Schenkel im Goldenen Schnitt

Kaschube nutzte 1717 das geometrische Mittel
($|\mathrm {\overline {GI}} |$ von $|\mathrm {\overline {BG}} |$ und $|\mathrm {\overline {AB}} |$) sowie „diesen Schnitt den goldenen“ als Konstruktionselement.
$|\mathrm {{\overline {KA}}|\;:\;|{\overline {AM}}|=|{\overline {BE}}|\;:\;|{\overline {EA}}|=|{\overline {KF}}|\;:\;|{\overline {FB}}} |$

Von M. Johann Wentzel Kaschube stammt die im Folgenden beschriebene und im Anschluss konstruktiv dargestellte geometrische Aufgabe aus dem Jahr 1717.

„§.34. Einen gleichschencklichten $\Delta$, in welchem der auf einem Schenckel stehende perpendicul $\mathrm {AB} =a$ gegeben, so den Schenckel $\mathrm {KM}$ selbst in $\mathrm {A}$ auf solche Arth schneidet, wie er von den übrigen perpend. Linien in $\mathrm {E}$ geschnitten wird, kan auf folgende Weise gefunden werden. […]“

– M. Johann Wentzel Kaschube: Cursus mathematicus, oder Deutlicher Begrief der Mathematischen Wissenschaften

Gesucht ist also ein gleichschenkliges Dreieck, in dem eine gegebene Strecke $\mathrm {\overline {AB}}$ sowie ein Schenkel des Dreiecks zueinander orthogonal sind und der Punkt $\mathrm {A}$ diesen Schenkel im Verhältnis des Goldenen Schnitts teilt.

Konstruktionsbeschreibung
(Angelehnt an die Beschreibung des Originals, die darin erwähnte Fig. 7 ist auf Tab. I Alg. Fig. 8)

Zuerst wird die Strecke $\mathrm {\overline {AB}}$ mit der frei wählbaren Länge $a$ senkrecht auf die Gerade $g$ errichtet. Es folgt das rechtwinklige Dreieck $\mathrm {ABC}$, in dem die Seite $\mathrm {\overline {AC}}$ mit Länge ${\tfrac {a}{2}}$ auf der Geraden $\mathrm {g}$ liegt. Der Kreisbogen um $\mathrm {C}$ mit Radius $|\mathrm {\overline {AC}} |$ ergibt Schnittpunkt $\mathrm {D}$, der Kreisbogen um $\mathrm {B}$ mit Radius $|\mathrm {\overline {BD}} |$ teilt in $\mathrm {E}$ die Seite $\mathrm {\overline {AB}}$ im Goldenen Schnitt. Ziehe einen Kreis um $\mathrm {E}$ mit Radius $\mathrm {\overline {EA}}$, ergibt Schnittpunkt $\mathrm {G}$ und einen Kreisbogen um $\mathrm {E}$ mit Radius $|\mathrm {\overline {EB}} |$. Nun errichte eine Senkrechte auf $\mathrm {\overline {AB}}$ ab $\mathrm {G}$ bis sie den Kreisbogen in $\mathrm {I}$ schneidet. Mit $\mathrm {\overline {GI}}$ ist das geometrische Mittel der beiden Streckenlängen $|\mathrm {\overline {BG}} |$ und $|\mathrm {\overline {AB}} |$ bestimmt. Ein Kreisbogen um $\mathrm {B}$ mit Radius $|\mathrm {\overline {GI}} |$ schneidet den Kreis um $\mathrm {E}$ in $\mathrm {F}$, und dabei ergibt sich das rechtwinklige Dreieck $\mathrm {EBF}$. Abschließend wird die Strecke $\mathrm {\overline {BF}}$ bis auf die Gerade $\mathrm {g}$ verlängert und um den soeben entstandenen Schnittpunkt $\mathrm {K}$ ein Kreisbogen mit Radius $|\mathrm {\overline {KB}} |$ gezogen, bis er die Gerade $\mathrm {g}$ in $\mathrm {M}$ schneidet.

Im somit gefundenen gleichschenkligen Dreieck $\mathrm {KMB}$ teilt der Punkt $\mathrm {A}$ der Senkrechten $\mathrm {\overline {AB}}$ den Schenkel $\mathrm {\overline {KM}}$ im Goldenen Schnitt.

$|\mathrm {\overline {KA}} |\;:\;|\mathrm {\overline {AM}} |=|\mathrm {\overline {BE}} |\;:\;|\mathrm {\overline {EA}} |=|\mathrm {\overline {KF}} |\;:\;|\mathrm {\overline {FB}} |$

Dreiecksfraktal

Dreiecksfraktal, Animation (am Ende mit 15 s Pause)

→ Hauptartikel: Fraktal

Ab 1975 sind in der Mathematik die unterschiedlichsten Fraktale entwickelt worden.

Das folgende Fraktal – mit sieben Iterationsschritten – verwendet ein gleichseitiges Dreieck als Ausgangsform. An seinen Ecken wird ein Dreieck mit einem bestimmten Verkleinerungsfaktor $\mathrm {f} \;\left(\mathrm {0<f<1} \right)$ Spitze an Spitze angehängt. Der Verkleinerungsfaktor $\mathrm {f}$ wird so gewählt, dass das Verhältnis der Seitenlängen zueinander dem Teilungsverhältnis $\Phi$ des Goldenen Schnittes entspricht.

Fraktale werden meist mithilfe eines Computers erstellt. Dieses zweidimensionale Dreiecksfraktal ist – mit entsprechendem Aufwand – auch als Konstruktion mit Zirkel und Lineal darstellbar.

Skizze

Skizze zur Festlegung der Kriterien, siehe hierzu auch Dreiecksfraktal, Potenzieren der Länge $\mathrm {f}$

Anhand der nebenstehenden Skizze wird der Verkleinerungsfaktor $\mathrm {f}$, die gewünschte Anzahl der Äste (Dreiecke) und somit auch der Abstand der letzten Äste zueinander grafisch bestimmt.

Es beginnt mit der Konstruktion eines gleichseitigen Dreiecks mit der Seitenlänge gleich $\mathrm {2}$. Halbiert man nun dessen beide Schenkel und zieht die Gerade $\mathrm {g}$ durch die soeben erhaltenen Mittelpunkte, ergibt sich das gleichseitige (grüne) Ausgangsdreieck des Fraktals mit Seitenlänge gleich $\mathrm {1}$. Es folgen zwei Verbindungslinien, jeweils ab dem Mittelpunkt der Schenkel bis zur gegenüberliegenden Ecke des Dreiecks. Sie schneiden sich im Mittelpunkt des Umkreises des großen Dreiecks. Beim Ziehen des Umkreises ergibt sich, mittels der Schnittpunkte auf der Geraden $\mathrm {g}$, der gesuchte Verkleinerungsfaktor $\mathrm {f}$ links und rechts vom Ausgangsdreieck.

Nachweis des Verkleinerungsfaktors f

Graph der kubischen Gleichung

Die oben beschriebenen Konstruktionsschritte gleichen denen der Konstruktion nach Odom.

Somit gilt in diesem Fall:

${\frac {1}{\mathrm {f} }}={\frac {\mathrm {1+f} }{1}}=\Phi$

daraus folgt

$\mathrm {f} =\Phi -1={\frac {1}{\Phi }}=0{,}6180339887\ldots$

Die in der Skizze mit gepunkteten Linien angedeutete Konstruktion zeigt: Die Seitenlängen (Kreisradien) für die nachfolgenden, noch gut im Fraktal erkennbaren Dreiecke, ergeben sich, indem man für das nächste Dreieck den Exponent des Verkleinerungsfaktors $\mathrm {f}$ um $\mathrm {1}$ erhöht:

$\mathrm {f^{2},\;f^{3},\;f^{4},\;f^{5},\;f^{6},\;f^{7}} \ldots$

Beutelspacher ermittelte in Der Goldene Schnitt den Wert des Abstandes, bei dem sich die entgegenkommenden Äste im Grenzfall berühren, letztendlich aus der kubischen Gleichung (siehe nebenstehendes Bild)

$\mathrm {f^{3}} +2\mathrm {f^{2}} -1=0$;

deren einzige positiven Lösung ist

$\mathrm {f} ={\frac {1}{\Phi }}$.

Somit ist aufgezeigt: $\mathrm {f}$ ist nicht nur der Wert des Verkleinerungsfaktors, sondern auch der Wert des Abstandes, bei dem sich im Grenzfall die einzelnen Äste berühren, sprich gerade noch nicht überlappen.

Papier- und Bildformate

Im Buchdruck wurde gelegentlich die Nutzfläche einer Seite, der sogenannte Satzspiegel, so positioniert, dass das Verhältnis von Bundsteg zu Kopfsteg zu Außensteg zu Fußsteg sich wie $2:3:5:8$ verhielt. Diese Wahl von Fibonacci-Zahlen approximiert den Goldenen Schnitt. Eine solche Gestaltung wird auch weiterhin in Teilen der Fachliteratur zum Buchdruck empfohlen.

Anwendung in der bildenden Kunst

→ Hauptartikel: Goldener Schnitt in der Kunst

Seit dem 19. Jahrhundert wurde der Goldene Schnitt zunächst in der ästhetischen Theorie (Adolf Zeising) und dann auch in künstlerischer, architektonischer und kunsthandwerklicher Praxis als ein ideales Prinzip ästhetischer Proportionierung bewertet. Er soll besonders angenehm, ansprechend, ausgewogen, harmonisch und schön wirken. Es gibt allerdings keinen empirischen Beleg für eine besondere ästhetische Wirkung, die von Proportionen des Goldenen Schnittes ausgeht. Schon der Begründer der empirischen Ästhetik, Gustav Theodor Fechner, stellte aufgrund eigener Experimente fest: „Hiernach kann ich nicht umhin, den ästhetischen Wert des Goldenen Schnittes … überschätzt zu finden.“

Architektur

→ Hauptartikel: Proportion (Architektur)

Goldenes Dreieck und Goldenes Rechteck in der Fassade der Kathedrale Notre-Dame de Paris