Hasta finales del siglo XIX, ningún matemático había logrado describir el infinito más allá de la idea de que es un valor absolutamente inalcanzable. Georg Cantor fue el primero en abordar a fondo un concepto tan abstracto; y lo hizo desarrollando la Teoría de conjuntos, que le llevó a la sorprendente conclusión de que hay infinitos de distintos tamaños. Ante el rechazo a esas ideas poco intuitivas, Cantor dudó de sí mismo y sufrió sucesivas crisis nerviosas, hasta morir internado en un psiquiátrico. Hoy en día, no se entienden las matemáticas sin sus revolucionarios trabajos.

Aunque nació en San Petersburgo (Rusia) — a donde sus padres habían emigrado desde Dinamarca—, Georg Cantor (3 de marzo de 1845-6 de enero de 1918) pasó la mayor parte de su vida en Alemania. El infinito le interesó desde joven, y siendo un treintañero publicó los artículos que desarrollaron su Teoría de conjuntos, en la que formalizó diversas ideas sobre el infinito matemático. Para Cantor, los conjuntos son colecciones de objetos que pueden poseer finitos o infinitos elementos. Por ejemplo, el conjunto de los dedos de una mano tiene finitos elementos ({pulgar, índice, corazón, anular y meñique}), mientras que el conjunto de los números naturales (N = {0, 1, 2, 3, 4, 5, 6…}) tiene infinitos elementos. Cantor estableció el concepto de cardinal como el número de elementos que tiene un conjunto: siguiendo con el mismo ejemplo, el cardinal del conjunto de los dedos de una mano es cinco (5) y el cardinal del conjunto de los números naturales es infinito (∞). Su colega Richard Dedekind, con el que se carteó durante años, ya había considerado los conjuntos infinitos en 1872; pero Cantor, además, se dio cuenta de que no todos los conjuntos infinitos son del mismo tamaño. Es decir, hay conjuntos infinitos que poseen distintos cardinales.
Funciones biunívocas
Podría parecer que el conjunto de los número naturales (N = {0, 1, 2, 3, 4, 5, 6…}) comprende más elementos que el subconjunto que contiene de números primos (P = {2, 3, 5, 7, 11, 13…}). Sin embargo, Cantor demostró que los dos tienen el mismo cardinal, y por tanto el mismo número infinito de elementos. Para ello emparejó cada uno de los elementos que forman un conjunto con los elementos del otro, lo que se conoce como establecer una función biunívoca entre ambos conjuntos. En el caso de los naturales y los primos el emparejamiento podría ser 0-2, 1-3, 2-5, 3-7, 4-11, 5-13, …
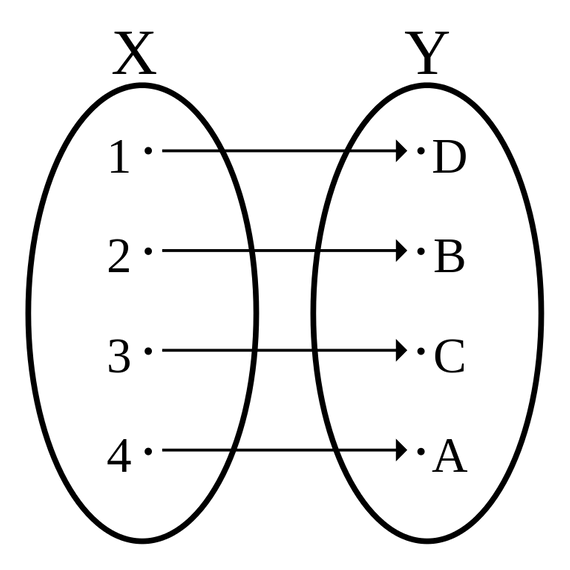
Por el contrario, en una de sus demostraciones más famosas, Cantor comprobó que era imposible establecer una función biunívoca entre el conjunto de los números naturales y el conjunto de los puntos que forman la recta real. Llegó así a la conclusión de que el cardinal del conjunto de los números reales era mayor que el de los números naturales: eran infinitos de distintos tamaños. Demostró aún más, que al cardinal infinito de los números reales le sigue otro mayor, y a su vez a este le sigue otro aún mayor, y así sucesivamente. Al más pequeño de todos estos cardinales infinitos, el cardinal de los números naturales, lo llamó Álef 0 (álef es la primera letra del alfabeto hebreo). A los siguientes los llamó Álef 1, Álef 2, Álef 3, etc. Todos estos cardinales de conjuntos infinitos se conocen por el nombre de cardinales transfinitos.

Algunos de los resultados de la Teoría de conjuntos eran realmente sorprendentes y chocaban contra la intuición, por lo que Cantor pidió en más de una ocasión a Dedekind que revisase sus demostraciones. También tuvo que invertir mucho esfuerzo en convencer a otros colegas matemáticos más escépticos. A raíz de sus descubrimientos, Cantor acabó desarrollando una aritmética transfinita completa, que equiparaba las operaciones de suma y multiplicación de los números naturales a los cardinales infinitos que definió. Cada número natural se puede identificar con el cardinal de un conjunto finito. Como decíamos, el 5 se puede identificar con el cardinal del conjunto de los dedos de una mano. Así, Cantor define las operaciones de suma y multiplicación de números como si fuesen operaciones entre los cardinales de conjuntos, ya sean finitos o infinitos.
El inicio de las crisis nerviosas
Cantor, y también Dedekind, fueron matemáticos excepcionales en su época, pero ninguno logró nunca una posición profesional destacada. Mientras Cantor permaneció casi toda su vida en la Universidad de Halle, una pequeña institución; Dedekind no pasó de profesor de secundaria en su ciudad natal, Brunswick. El principal detractor de Cantor fue Leopold Kronecker, que le impidió ingresar en la prestigiosa Universidad de Berlín todas las veces que lo intentó. Kronecker defendía que las matemáticas debían basarse en los números enteros, y rechazaba de forma sistemática aquella incipiente nueva rama de las matemáticas. Los ataques de Kronecker acabaron por provocar en 1884 la primera de las crisis nerviosas de Cantor, que padeció periódicamente durante el resto de su vida.

Cantor pasó el final de sus días en un psiquiátrico de Halle, donde murió. Sin embargo, su Teoría de conjuntos acabó convirtiéndose en el lenguaje común empleado en las diversas ramas de las matemáticas actuales. Pocos años después de su muerte, el reconocido matemático David Hilbert aseguró que la aritmética transfinita es «el más sorprendente producto del pensamiento matemático y una de las realizaciones más bellas de la actividad humana».
Comentarios sobre esta publicación