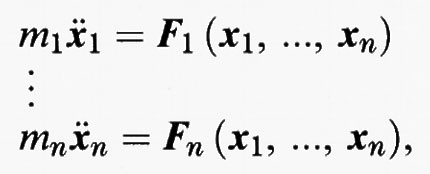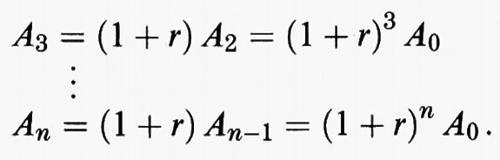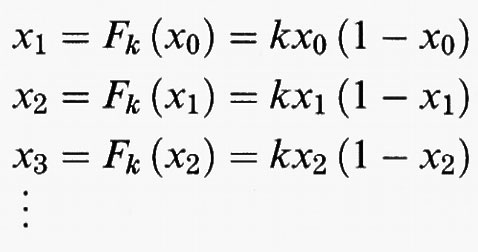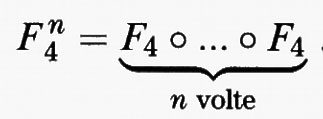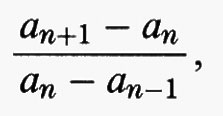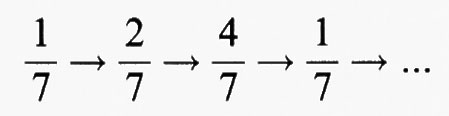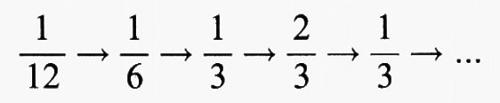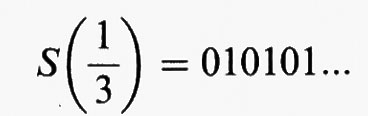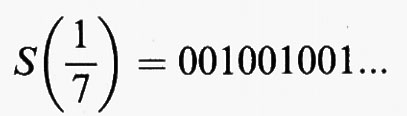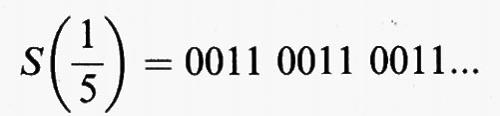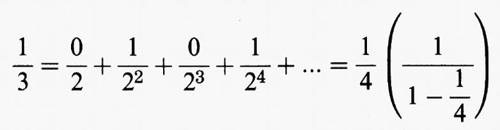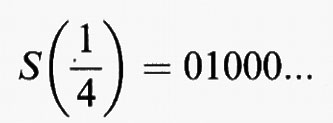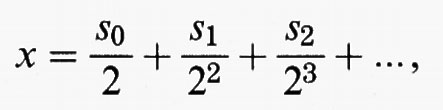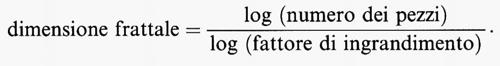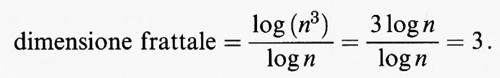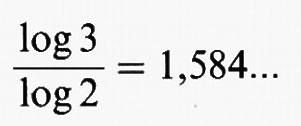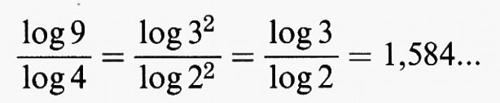Caos

Caos

Introduzione storica

Secondo l'accezione più comune, il termine ‛caos' significa totale annientamento dell'ordine o assenza di qualsiasi struttura. Analogamente, in matematica, e più in generale in ogni scienza, la presenza del ‛caos' implica la totale impossibilità di predire il risultato di qualsiasi evento. Tuttavia, come vedremo in seguito, la moderna ‛teoria del caos' si basa, forse paradossalmente, sul fatto che i sistemi caotici hanno spesso una struttura incredibilmente ricca. In un sistema caotico può rivelarsi impossibile predire uno specifico avvenimento, e tuttavia la totalità dei possibili risultati è spesso dotata di una elegante struttura perfettamente comprensibile.

L'interesse per il caos ha inizio alla fine del secolo scorso. Il grande matematico francese Henri Poincaré si era dedicato allo studio del comportamento delle soluzioni del problema degli n-corpi. Anch'egli, come tutti gli scienziati del suo tempo, prevedeva che prima o poi sarebbe stata trovata una soluzione completa di questo problema, per cui le orbite seguite dai pianeti si sarebbero sempre trovate su superfici sufficientemente regolari e facilmente identificabili nell'insieme di tutte le configurazioni possibili. Egli presumeva che il sistema sarebbe stato ‛integrabile'. Una condizione necessaria per l'integrabilità avrebbe dovuto essere il perfetto raccordo di certi insiemi di curve-soluzione, che oggi sono dette varietà stabili e varietà instabili. Nel XIX secolo nessuno aveva mai preso in considerazione l'ipotesi che le cose non stessero così. Ma non Poincaré, il quale in un lavoro lungimirante che gli procurò anche un premio (v. Poincaré, 1890), si chiese che cosa sarebbe accaduto se queste due varietà si fossero incrociate formando un angolo, ossia trasversalmente, secondo la terminologia odierna. Una volta ammessa questa possibilità, Poincaré comprese che il sistema dinamico avrebbe ammesso soluzioni estremamente irregolari e si rese conto anche che, per comprendere un tipo di comportamento così intricato, ci sarebbero voluti anni.

Poincaré aveva visto giusto: ci vollero quasi settanta anni prima che i matematici si rendessero conto delle difficoltà che lui aveva intuito nel 1890. Furono infatti due importanti scoperte, negli anni sessanta del nostro secolo, ad aprire la via alla comprensione del caos. La prima si deve a E. N. Lorenz (v., 1963), un meteorologo del Massachusetts Institute of Technology, negli Stati Uniti, il quale, cercando di far luce sui problemi di idrodinamica connessi con la previsione del tempo, decise di semplificarne il più possibile il modello matematico. Invece di studiare un'equazione alle derivate parziali o un sistema di ordine elevato di equazioni differenziali ordinarie, Lorenz prese in esame un sistema di 3 equazioni differenziali dato da:

ú = σ (y - x)

ÿ = ρx - y - xz

ä = βz + xy

dove β, ρ e σ sono costanti positive. Si osservi che questo sistema possiede soltanto due termini quadratici, xz e xy.

Negli anni sessanta Lorenz poteva disporre di un computer, anche se piuttosto rudimentale, con il quale tracciò ampi tratti delle curve-soluzione rilevando comportamenti complicati, ma non del tutto imprevisti. Ma qualcosa di assolutamente imprevisto accadde quando decise di ricalcolare una delle soluzioni. Invece di servirsi dei dati iniziali completi, che avevano portato alla soluzione originale, Lorenz utilizzò soltanto il troncamento che appariva sullo schermo, tralasciando parecchie cifre che comparivano al quarto e al quinto posto della rappresentazione decimale. Quando ricalcolò lo sviluppo della nuova soluzione si accorse che questa era più o meno uguale alla prima, ma solo fino a un certo punto, dopo il quale le due curve divergevano fino a non avere più alcuna somiglianza tra di loro. Lorenz aveva scoperto la caratteristica essenziale di un sistema caotico: la dipendenza sensibile dalle condizioni iniziali, per cui mutamenti minimi nella posizione di partenza della curva-soluzione possono portare a risultati estremamente diversi, rendendo così quasi impossibile la previsione dell'andamento remoto delle soluzioni.

In quegli stessi anni, anche Stephen Smale, un matematico dell'Università della California a Berkeley, affrontava il caos, anche se in modo diverso, e cioè considerando sistemi dinamici discreti anziché governati da equazioni differenziali. Egli pensò che il comportamento complesso in cui si era imbattuto Poincaré, a lui ben noto, fosse in realtà un comportamento atipico che poteva essere considerato un'aberrazione. Nel tentativo di spiegare le varietà di Poincaré, stabili e instabili, che si incrociavano, escogitò un esempio che è oggi noto come ‛applicazione a ferro di cavallo' (v. Smale, 1965). Questa semplificazione della varietà di Poincaré permise a Smale di comprendere chiaramente la totalità dei movimenti caotici che Poincaré aveva osservato. Anche se le soluzioni del sistema presentavano di fatto una dipendenza sensibile dai dati iniziali, le idee di Smale mostravano l'esistenza, nel quadro totale, di un qualche tipo di configurazione e di struttura particolari.

In tempi più recenti, il computer e la grafica hanno avuto un'influenza determinante nello studio dei sistemi caotici. Tramite il computer si è scoperta la presenza di qualche forma di caos in molti sistemi. Ancora più importante è il fatto che, per mezzo della grafica, si sia riusciti a mostrare che i sistemi caotici, se osservati dal punto di vista geometrico, rivelano spesso regolarità nascoste. Le immagini del computer, dette frattali (v. cap. 8), mostrano una quantità affascinante di dettagli in ogni scala di ingrandimento. Lo studio dei frattali - termine coniato da Benoît Mandelbrot (v., 1982) - si è sviluppato di pari passo con quello del caos.

I sistemi dinamici

Il caos è un argomento che appartiene a buon diritto a quel settore della matematica noto come teoria dei sistemi dinamici o, più precisamente, alla teoria dei sistemi dinamici non lineari. Un sistema dinamico è costituito da uno o più processi che mutano nel tempo. Il movimento dei pianeti attorno al Sole è un esempio di sistema dinamico studiato fin dall'antichità, e così i flussi e i riflussi delle maree, i rialzi e i ribassi della borsa, i temporali e le bonacce, sono tutti esempi di processi che si evolvono nel tempo e pertanto rappresentano sistemi dinamici.

Chi si trovi a studiare un sistema dinamico in laboratorio o nella vita reale, vorrebbe naturalmente poter predire quale sarà il risultato dell'azione del sistema. Il tempo sarà piovoso o sereno tra due settimane? La borsa sarà in ribasso o in rialzo? Sarà mai possibile che la Terra entri in collisione con un altro pianeta o che precipiti sul Sole?

Dagli esempi che abbiamo ora indicato risulta chiaro che certi sistemi dinamici sono completamente prevedibili. Il Sole sorgerà domani mattina. Le maree saliranno o caleranno secondo un orario e un calendario ben noti. Tuttavia, altri sistemi dinamici sono assolutamente imprevedibili. Le condizioni atmosferiche rappresentano un esempio classico: chi può prevedere se tra due settimane ci sarà il sole o pioverà? Analogamente, sistemi economici quali il mercato azionario sfidano qualsiasi previsione.

È naturale chiedersi allora perché certi sistemi dinamici sembrino perfettamente prevedibili mentre altri non lo sono. Dagli esempi citati si direbbe che il problema della prevedibilità sia in relazione al numero delle variabili dalle quali dipende il sistema. Per quanto riguarda i pianeti, il loro numero è finito, e pertanto il sistema è soggetto soltanto a un piccolo numero di forze distinte. Per comprendere i movimenti delle maree, è sufficiente considerare la posizione della Terra, della Luna e del Sole. Invece, per una previsione meteorologica accurata è essenziale una conoscenza dettagliata della velocità e della direzione del vento, della pressione atmosferica, della temperatura e di molti altri parametri rilevati in ogni punto della Terra. Allo stesso modo, per poter prevedere l'andamento della borsa è necessario essere al corrente dei traguardi a breve termine di tutti gli operatori presenti sul mercato.

Sembra dunque che il problema della prevedibilità o imprevedibilità di un certo sistema dinamico dipenda dal numero delle variabili, sia esso il numero dei pianeti che interagiscono tra di loro, o quello degli operatori di borsa. Minore è il numero delle variabili, maggiore è dunque la prevedibilità.

Di fatto, niente potrebbe essere più lontano dal vero. Esistono numerosi sistemi dinamici che dipendono da un numero ristretto di variabili, taluni da una sola variabile, e che tuttavia si comportano in modo altrettanto imprevedibile del tempo atmosferico e altrettanto caotico del mercato azionario. Lo studio di questi sistemi semplici ma imprevedibili è oggi noto come ‛teoria del caos'.

Esistono molti tipi diversi di sistemi dinamici e forse quelli più importanti sono regolati da equazioni differenziali. Si tratta di sistemi che cambiano con continuità col passare del tempo. Il moto dei pianeti, per esempio, è governato da un sistema di equazioni differenziali, che rappresenta il cosiddetto problema degli n-corpi, dove il moto di ciascun pianeta è determinato dalla legge di Newton F = ma. In questo caso, F è la somma delle forze che agiscono sul pianeta e che esprimono le attrazioni gravitazionali esercitate dagli altri pianeti, mentre m è la massa del pianeta e a la sua accelerazione. Se x_i = x_i (t) è la posizione del pianeta i-esimo nello spazio ordinario, l'accelerazione è data da x¨ _i (t), la derivata seconda di x_i (t) rispetto al tempo. Si ottiene così un sistema di 3n equazioni differenziali ordinarie del secondo ordine:

che rappresenta il modello matematico del moto planetario.

In questo modello abbiamo fatto un certo numero di ipotesi semplificatrici, tra le quali quella di non poco conto secondo cui ciascun pianeta è un ‛punto materiale'. Malgrado ciò, il problema generale degli n-corpi resta un problema irrisolto nel caso in cui sia n ≥ 3.

Nel caso di sistemi fisici più complessi, come quelli che si incontrano in idrodinamica o nella meteorologia e che dipendono di solito da un numero infinitamente maggiore di variabili, il modello del sistema è in genere descritto da equazioni alle derivate parziali anziché da equazioni differenziali ordinarie. La soluzione di questi sistemi è ancora più difficile.

All'estremità opposta si trovano sistemi che cambiano in modo discreto, ossia a intervalli di tempo determinati, e che sono intrinsecamente più facili da trattare. Un esempio semplice può essere quello di un libretto di risparmio sul quale vengono periodicamente versati gli interessi. Se A_n indica la somma depositata sul libretto alla fine dell'n-esimo periodo di tempo, che potrebbe essere l'n-esimo mese o l'n-esimo quadrimestre a seconda delle modalità di versamento degli interessi, e se supponiamo che il tasso di interesse sia r, dopo il primo intervallo di tempo l'ammontare dei risparmi è:

A₁ = (1 + r) A₀.

Dopo il secondo, l'ammontare è:

A₂ = (1 + r) A₁ = (1 + r)² A₀

e così via,

Questo è un esempio di processo iterativo o di sistema dinamico discreto. Si tratta di un sistema lineare in quanto A_n dipende linearmente dal saldo dell'intervallo precedente:

A_n = (1 + r) A_n-1.

Un esempio di processo iterativo non lineare è offerto dal problema della previsione di crescita o calo della popolazione di una certa specie. Il modello più semplice è il modello di crescita esponenziale, nel quale si suppone che la popolazione P_n al momento della n-esima generazione sia proporzionale alla popolazione della generazione precedente:

P_n = kP_n-1.

Anche questo è un sistema dinamico lineare per il quale è possibile predire l'aumento della popolazione:

P_n = kⁿP₀.

Se dunque k > 1 (e se supponiamo che sia P₀ > 0), si finirà con l'avere un'esplosione demografica. Se 0 〈 k 〈 1, la popolazione si estinguerà. Infine, se k = 1, la popolazione rimarrà costante.

È chiaro che il modello della crescita esponenziale non permette una previsione soddisfacente della crescita di una popolazione. Una delle ragioni è che nessuna popolazione può crescere senza controllo per molte generazioni. Quando la popolazione diviene troppo numerosa, la sovrappopolazione e la mancanza delle risorse necessarie determinano una modifica del tasso di crescita.

Un modello semplice di crescita della popolazione che tenga conto della sovrappopolazione, è il modello logistico

P_n = kP_n-1 (1 - P_n-1),

ove P_n è non tanto la popolazione realmente vivente nella generazione n, quanto la frazione della popolazione massima possibile in grado di sopravvivere in quella generazione. In altri termini, P_n rappresenta la probabilità di sopravvivenza per la n-esima generazione. Di conseguenza, i valori di P_n possibili sono 0 ≤ P_n ≤ 1; P_n = 1 indica una grave sovrappopolazione e P_n = 0 corrisponde all'estinzione. La costante k viene di solito scelta tra 0 e 4. Questo rappresenta un sistema dinamico non lineare, in quanto P_n non dipende linearmente da P_n-1, bensì

P_n = kP_n-1 - kP²_n-1

a causa della presenza del termine quadratico P²_n-1. Mentre a prima vista potrebbe sembrare che questa modificazione apparentemente marginale del modello di crescita esponenziale non conduca a comportamenti sostanzialmente diversi, in realtà questo semplice sistema dimostra di possedere (per molti valori di k) quell'alto grado di imprevedibilità che è la caratteristica precipua del caos.

3. Il modello logistico per la crescita di una popolazione

Per comprendere e predire il comportamento della popolazione, è necessario a questo punto introdurre alcuni termini.

Consideriamo la funzione:

F_k = kx (1 - x).

Dall'iterazione di questa funzione, si derivano le successive generazioni; vale a dire, data una popolazione iniziale x₀, si calcola in successione

La successione numerica degli x₀, x₁, x₂ , ..., si chiama l'orbita di x₀ rispetto a F_k. Per valori diversi di k, le orbite di F_k possono comportarsi in modo stabile e prevedibile, oppure in modo caotico e imprevedibile, come risulta evidente da un'analisi grafica.

Nella fig. 1 è tracciato il grafico di F₁ (x) = x (1 - x) per 0 ≤ x ≤ 1, al quale abbiamo aggiunto la diagonale y = x. Per disegnare l'orbita di x₀, basta tracciare una retta verticale dal punto (x₀, x₀) sulla diagonale, fino al punto [x₀, F₁ (x₀)] sul grafico di F₁, ottenendo così il punto (x₀, x₁). Si traccia poi una retta orizzontale che incontra la diagonale nel punto (x₁, x₁). Si itera questo processo tracciando una retta verticale da (x₁, x₁) fino a (x₁, x₂), poi una retta orizzontale da (x₁, x₂) a (x₂, x₂). All'estremo di ciascun segmento orizzontale si trova il punto (x_n, x_n) e si determina così l'n-esimo punto nell'orbita di x₀.

Si osservi che il grafico di F₁ sta interamente sotto la diagonale. Questo fa sì che tutte le orbite decrescano al crescere di n. L'analisi grafica nella fig. 1 indica che tutte le orbite tendono a 0, e pertanto questo particolare modello predice l'estinzione della specie.

Al crescere di k, si incontrano diversi comportamenti dinamici. Per esempio, se k = 2 si ha un punto fisso per l'iterazione in x₀ = 1/2, in quanto F₂ (1/2) = 1/2. Ciò significa che una popolazione che rappresenti il 50% della popolazione massima è in questo modello in posizione di equilibrio. L'analisi grafica  mostra che ogni altra orbita tende verso questo punto fisso, nel senso che x_n → 1/2 per n → ∞. In questo senso il punto fisso è stabile: qualsiasi altra popolazione iniziale nelle sue vicinanze avrà lo stesso destino di x₀ = 1/2.

Quando k cresce fino a 3,2 si osserva un fenomeno diverso: anziché tendere al punto fisso, molte orbite tendono a oscillare con periodo 2. Esiste un'orbita, precisamente x₀ = 0,513 e x₁ = 0,7995, che è un 2-ciclo. È facile vedere che:

x₁ = F_3,2 (x₀)

x₀ = F_3,2 (x₁)

cosicché l'orbita si riproduce ogniqualvolta l'operazione viene ripetuta: x₀, x₁, x₀, x₁ , ... Come appare dall'analisi grafica, gran parte delle altre orbite raggiunge alla fine questo 2-ciclo.

Se si aumenta il parametro k fino a 3,5 le cose cambiano ancora. Invece di un'orbita con periodo 2, le orbite ora tendono verso un ciclo con periodo 4, come risulta dalla fig. 4. E così di seguito. Al crescere del parametro k, troviamo una successione di valori per i quali le orbite non sono più attratte da un ciclo di periodo 2^n-1, ma da un ciclo di periodo 2ⁿ. Questi valori di k si chiamano ‛punti di biforcazione' e il fenomeno prende il nome di ‛biforcazione con raddoppio del periodo'.

Per valori ancora maggiori di k, il comportamento cambia nuovamente. Per esempio, per k = 4 non è possibile distinguere, attraverso un'analisi grafica, un andamento particolare per l'orbita di un dato iniziale tipico.Anzi, quest'orbita sembra capitare all'interno di ogni sottointervallo, per quanto piccolo, dell'intervallo originale 0 ≤ x ≤ 1. Questa è una delle caratteristiche del comportamento caotico.

Peraltro, non tutte le orbite di F₄ si comportano in questo modo. Per esempio, tanto 0 che 3/4 sono punti fissi. Anche il dato iniziale x₀ = 1/2 finisce per essere fissato e la sua orbita è 1/2, 1, 0, 0, 0, ... Per questa iterazione, l'analisi grafica mostra la presenza di un 2-ciclo e di un 3-ciclo.

Tuttavia, la maggior parte delle orbite sembra non avere alcun tipo di regolarità, come si scopre anche in altro modo e cioè tracciando un istogramma dei primi 20.000 punti sull'orbita di un punto iniziale scelto a caso nell'intervallo 0 〈 x 〈 1. Con probabilità 1, si ottiene l'immagine rappresentata nella fig. 7, il che indica ancora una volta come le orbite abbiano un andamento irregolare nell'intervallo, senza mai diventare periodiche o tendere a orbite periodiche.

Un'orbita che gode della proprietà di avere almeno un punto in ogni sottointervallo arbitrariamente piccolo di 0 ≤ x ≤ 1 prende il nome di ‛orbita densa'. È noto che esistono orbite dense per F₄ (x) = 4x (1 - x). Di fatto l'orbita tipica per F₄ è densa in 0 ≤ x ≤ 1.

Tuttavia, come si è visto nella fig. 6, ci sono anche altre orbite. Per F₄, esiste un numero infinito di cicli con periodi arbitrariamente grandi. Ciò si vede in modo efficace tracciando i grafici di F₄ o F₄, F₄ o F₄ o F₄, e così via. I punti che stanno in un n-ciclo appartengono all'intersezione della diagonale y = x con il grafico di:

Come si rileva dalla fig. 8, il grafico di F4ⁿ interseca la diagonale in 2ⁿ punti; il che dimostra l'esistenza di un numero infinito di punti periodici per F₄. Ma c'è dell'altro: l'insieme di tutti i punti che appartengono a un ciclo per F₄ è denso in 0 ≤ x ≤ 1, ossia ogni sottointervallo per quanto piccolo di 0 ≤ x ≤ 1 contiene almeno uno (ma di fatto un numero infinito) di punti periodici.

Questi due fatti sono un indizio delle dinamiche complicate presenti nelle iterazioni di F₄. Se consideriamo un qualsiasi punto x₀ nell'intervallo 0 ≤ x ≤ 1 e un qualsiasi numero δ > 0 arbitrariamente piccolo, possiamo trovare all'interno dell'intervallo di centro x₀ e ampiezza 2δ: 1) un numero infinito di punti periodici distinti; 2) un numero infinito di punti distinti le cui orbite sono dense in 0 ≤ x ≤ 1. La coesistenza di due comportamenti dinamici così diversi l'uno dall'altro costituisce una delle componenti principali del caos.

Una importante proprietà di un sistema caotico è la dipendenza sensibile dalle condizioni iniziali, alla quale abbiamo accennato in precedenza. Nella fig. 9 sono riportate le orbite rispetto a F₄ di quattro diversi punti iniziali, o semi. L'orbita di 0,5 è semplice: 0,5, 1, 0, 0, 0, ... Si osservi tuttavia quanto sono diverse le orbite che nascono da condizioni iniziali vicine: 0,49, 0,499 e 0,4999. Dopo un numero relativamente piccolo di iterazioni, queste orbite non presentano più alcun tipo di somiglianza. Mentre l'orbita di 1/2 si stabilizza nel punto 0, le altre sono alla fine ‛molto distanti' l'una dall'altra, e la distanza è talora prossima a 1.

Di fatto si può dimostrare che F₄ presenta veramente questo tipo di dipendenza sensibile nella vicinanza di ogni punto dell'intervallo. Più esattamente, c'è un numero β > 0 tale che, per ogni punto x₀ nell'intervallo 0 ≤ x ≤ 1 e ogni δ > 0, esiste un punto y₀ che dista da x₀ meno di δ, per il quale è ∣y_n - x_n∣ > β per qualche n. In altre parole, dato un qualsiasi punto iniziale x₀, esiste sempre nelle sue vicinanze un punto iniziale y₀ la cui orbita finisce per allontanarsi per un valore superiore a β da quella di x₀. Dipendenza sensibile, densità dei punti periodici ed esistenza di un'orbita densa concorrono a determinare una possibile definizione di caos. Non tutti gli autori tuttavia concordano su questa definizione: per alcuni è necessaria soltanto la dipendenza sensibile, altri non ritengono necessaria la densità dei punti periodici, e altri ancora esigono una forma più forte di dipendenza sensibile, che si riallaccia agli ‛esponenti positivi di Liapounov'. Resta il fatto, tuttavia, che la coesistenza di dipendenza sensibile, orbita densa e un insieme denso di punti periodici indica che le dinamiche della semplice espressione F₄ (x) = 4x (1 - x) non sono affatto semplici da dominare. L'aver compreso che molti sistemi dinamici semplici quanto questa funzione logistica possono comportarsi in modo così caotico costituisce una delle più interessanti scoperte della matematica del XX secolo.

La transizione al caos e il numero di Feigenbaum

Nel capitolo precedente abbiamo osservato come la famiglia delle funzioni logistiche dia luogo, col crescere del parametro k, a una serie di biforcazioni con raddoppio del periodo. Quando k raggiunge il valore 4, la dinamica è già divenuta caotica. Di fatto, via via che il parametro si avvicina a 4, si verifica una serie di altri eventi, efficacemente illustrabili con un grafico. Nella fig. 10 abbiamo calcolato un'immagine nota come diagramma dell'orbita o diagramma di biforcazione. Questa figura mostra l'evoluzione di un'orbita particolare in funzione di k. Segniamo k sull'asse orizzontale, con k compreso tra 1 e 4. Sulla retta verticale passante per un certo valore di k, indichiamo la sorte dell'orbita di 1/2 sotto l'azione di F_k, riportando soltanto gli ultimi 300 punti. Questo ci permette di vedere che cosa, alla fine, accade all'orbita. Si osservi che all'inizio F_k subisce una serie di raddoppi del periodo, come abbiamo già osservato nel capitolo precedente. In seguito, l'orbita apparentemente riempie un intervallo, o una coppia di intervalli, secondo quello che sembra essere un regime caotico. In questo regime caotico sembra tuttavia che vi siano finestre senza caos. Intorno a k = 3,83, si apre una finestra come quella che abbiamo ingrandito nella fig. 11; e questa finestra, così come il suo ingrandimento (v. fig. 12) assomiglia molto al diagramma dell'orbita originale.

È noto che queste finestre riempiono in realtà un insieme denso dell'intervallo nel quale varia il parametro. Sebbene sia difficile rilevarlo in un ingrandimento come quello della figura, esiste una finestra siffatta arbitrariamente vicina a ogni valore di k.

La struttura dinamica all'interno di ciascuna finestra (con l'eccezione della finestra che corrisponde al raddoppio del periodo originale) è molto ricca. È noto che esiste un ciclo iniziale attrattivo di un certo periodo, che in seguito subisce una successione di raddoppi di periodo fino a terminare nella propria banda caotica minima (naturalmente con altre finestre parzialmente sovrapposte). Ma c'è dell'altro. Esiste un insieme di Cantor per ciascun valore di k nella finestra in cui la dinamica è caotica. In questo insieme di Cantor si trovano infiniti altri punti periodici, e anche in questo caso la funzione rivela una dipendenza sensibile da questo insieme. Non è possibile visualizzare tutte queste complicazioni perché tutte le orbite in questione sono repulsive e pertanto invisibili al computer.

Si deve a Sarkovskii (v., 1964) un interessante teorema che illustra la struttura delle orbite periodiche all'interno di queste finestre. Il teorema può essere enunciato così: poniamo tutti i numeri naturali nell'ordine seguente,

che si chiama ordinamento di Sarkovskii. Sia F una qualsiasi funzione continua sulla retta reale o su un suo intervallo. Se F ha un ciclo di periodo n, e n viene prima di k nell'ordinamento di Sarkovskii, F ha anche un ciclo di periodo k. Si noti la potenza di questo teorema, che non dipende da alcuna ipotesi, se non dalla continuità. Per esempio, nell'ordinamento di Sarkovskii, 3 compare per primo e quindi, se F ha un ciclo di periodo 3, deve avere cicli di ogni altro periodo. Inoltre, se F ha un ciclo qualsiasi che non sia una potenza di 2, F deve avere un numero infinito di orbite periodiche. Si osservi che i periodi della forma 2ⁿ compaiono per ultimi nell'ordinamento di Sarkovskii. Questo è il motivo per cui la nostra famiglia logistica comincia con dinamiche semplici e con raddoppi di periodo.

Torniamo infine al regime di raddoppio di periodi nel diagramma delle orbite. Nella fig. 13 abbiamo ingrandito il periodo 2 e una porzione della parte di questo diagramma relativa al periodo 4. Osserviamo la somiglianza di queste immagini. Questa regolarità geometrica è la conseguenza di una scoperta importante di Feigenbaum (v., 1978). Per comprendere questo risultato, indichiamo con a_n il valore del parametro per cui ha origine il ciclo di periodo 2ⁿ. Gli a_n convergono a un valore limite a_∞ del parametro, e questa convergenza è geometrica. Ossia, se formiamo i rapporti

la successione così ottenuta tende a un limite e precisamente a 4,669201... Inoltre, per qualsiasi altra funzione che tenda a un regime caotico mediante una successione di raddoppi di periodo, questo limite esiste ed è sempre lo stesso. In particolare, nel raddoppio a cascata del periodo all'interno delle altre finestre nel diagramma dell'orbita, si trova lo stesso limite. Anche se di fatto la validità del risultato di Feigenbaum richiede che siano soddisfatte alcune ipotesi tecniche, è pur tuttavia vero che la maggior parte delle funzioni tende a un regime caotico secondo lo schema di Feigenbaum. Questo stesso numero è stato osservato anche in natura in certi esperimenti idrodinamici nei quali i fluidi diventano sempre più turbolenti tramite una successione di raddoppi di periodo.

Le implicazioni della dipendenza sensibile

La presenza della dipendenza sensibile dalle condizioni iniziali in un sistema dinamico ha conseguenze profonde a livello sia computazionale che filosofico. Dal punto di vista computazionale, come ci si può fidare di un elenco di numeri che descriva un'orbita? Dopo tutto, ogni calcolo è condizionato dalla approssimazione che gli viene imposta. Di conseguenza, se durante il calcolo di un'orbita si opera un troncamento o un'approssimazione ci si trova in presenza di un'orbita diversa la cui evoluzione è, forse, completamente differente. Questo potrebbe far sembrare i calcoli con i sistemi caotici del tutto inutili.

Facciamo adesso un secondo esempio e supponiamo che il sistema dinamico di cui ci occupiamo corrisponda a un sistema fisico reale. Poiché non è possibile misurare le condizioni iniziali di un tale sistema con precisione infinita, anche in questo caso sembrerebbe che qualsiasi calcolo o previsione per un sistema caotico debba quasi certamente condurre a risultati sbagliati. Ed è proprio così. Qualsiasi previsione della sorte di una specifica orbita in un sistema caotico va guardata con scetticismo. Paradossalmente, tuttavia, i dati che hanno origine dall'iterazione sono in un certo senso corretti. Uno dei motivi di questa peculiarità è dovuto a un risultato ottenuto da Bowen (v., 1978) secondo il quale, per certi sistemi caotici, esiste un'orbita reale che ‛insegue' l'orbita calcolata. Ciò significa che quest'ultima riflette il comportamento reale di una qualche orbita effettiva, nel senso che l'orbita calcolata resta, per tutte le iterazioni, prossima all'orbita reale. Naturalmente, è probabile che l'orbita reale non sia l'orbita del dato iniziale scelto, ma quella di un qualche dato vicino. Inoltre, sebbene i numeri che comprendono l'orbita calcolata siano quasi certamente errati, le ‛immagini' generate da quest'orbita sono quasi certamente corrette. Per esempio, si ottiene lo stesso istogramma, praticamente per qualsiasi punto iniziale, per la funzione logistica F₄ (x) = 4x (1 - x), sebbene la lista dei numeri che definiscono le orbite siano molto diversi.

Dal punto di vista filosofico, che implicazioni ha la dipendenza sensibile su principî tenuti da lungo tempo in alta considerazione come le leggi di Newton? Certamente, per i sistemi non caotici le leggi di Newton funzionano alla perfezione. Ma in un sistema caotico non si può nemmeno sperare di utilizzare le leggi di Newton per fare delle previsioni, semplicemente perché i calcoli sono condizionati da una approssimazione finita. Questo naturalmente non significa che le leggi non siano valide, ma solo che bisogna usare un'estrema cautela nell'interpretare il comportamento dei sistemi caotici. Per comprendere la dipendenza sensibile può essere utile ricorrere a un'analogia. Abitualmente si ritiene che i modelli meteorologici siano particolarmente sensibili alle condizioni iniziali. Questo è ciò che viene talvolta chiamato ‛effetto farfalla', in quanto il battito delle ali di una farfalla in Brasile può influenzare il clima a New York qualche tempo più tardi.

La funzione di raddoppio

Un esempio puramente matematico, ma non per questo meno tipico di un sistema dinamico caotico, è quello della funzione di raddoppio. Questo processo iterativo ha luogo nell'intervallo I definito da 0 ≤ x ≤ 1. La legge dell'iterazione è la seguente: dato x in questo intervallo, si scriva 2x, a meno che sia 2x ≥ 1. In quest'ultimo caso, si scriva 2x - 1 che si trova ancora in I. Più esattamente, la funzione di raddoppio è definita da:

Talvolta questa formula viene abbreviata scrivendo:

D (x) = 2x mod 1 .

Si osservi anzitutto che esistono molti punti periodici per D. Per esempio, l'orbita di 1/3 è 1/3, 2/3, 1/3, 2/3, ... che è un ciclo con periodo 2. L'orbita di 1/5 è un ciclo con periodo 4:

mentre l'orbita di 1/7 è un ciclo con periodo 3:

Di fatto se p/q è una frazione (ridotta ai minimi termini) con il denominatore dispari, l'orbita di p/q è necessariamente periodica. Questo mostra che i punti periodici della funzione di raddoppio formano un sottoinsieme denso di I. Se p/q è una frazione con denominatore pari, l'orbita di p/q finisce per diventare periodica. Per esempio l'orbita di 1/12 è:

che alla fine ha un andamento ciclico con periodo 2. Allo stesso modo 1/8 si trova su un'orbita che alla fine è fissa:

Poiché le frazioni di questa forma sono anch'esse dense in I, se ne deduce che alla fine anche i punti che danno origine a una periodicità formano un sottoinsieme denso dell'intervallo.

La funzione di raddoppio mostra chiaramente una dipendenza sensibile poiché, a ogni iterazione, la distanza tra due punti raddoppia, a meno che, naturalmente, i punti non si trovino da parti opposte rispetto al punto centrale 1/2. La funzione di raddoppio serve anche come modello semplificato dell'applicazione a ferro di cavallo di Smale, che negli anni sessanta fornì la prima descrizione completa di un sistema caotico. Per comprendere la dinamica della funzione di raddoppio, conviene utilizzare una descrizione un po' diversa di questa iterazione.

Teniamo presente che l'insieme sul quale è definita la funzione di raddoppio è l'intervallo I dato da 0 ≤ x 〈 1. Dividiamo ora questo intervallo in due parti: I₀ , dato da 0 ≤ x 〈 1/2, e I₁, dato da 1/2 ≤ x 〈 1. Per ciascun x in I è definito l'itinerario di x che è una successione infinita,

S (x) = s₀s₁s₂ ... ,

nella quale ciascun termine s_j è 0 oppure 1. Il termine s_j è 0 se il j-esimo punto dell'orbita di x sta in I₀; altrimenti s_j = 1. Per esempio:

poiché l'orbita di 1/3 è 1/3, 2/3, 1/3, 2/3, ... che salta a destra e a sinistra di 1/2. Allo stesso modo,

e

Quindi, a ciascun punto x in I è associata una successione infinita di 0 e di 1 che indica, grosso modo, la posizione di tutti i punti dell'orbita di x.

Esiste un'altra descrizione, forse più familiare, di questa successione di 0 e di 1: l'itinerario S(x) di x non è altro che la successione binaria associata a x. Infatti,

e

i numeratori di questi sviluppi rappresentano proprio l'itinerario del punto. Come è noto, esiste un'ambiguità nelle successioni binarie associate ai numeri razionali diadici della forma p/2ⁿ. Per esempio la successione binaria associata a 1/4 è 01000... oppure 001111... In virtù della definizione non vi è tuttavia alcuna ambiguità associata all'itinerario di tali numeri. Per esempio:

e

cioè per l'itinerario di un razionale diadico si sceglie sempre la successione che termina in una coda di 0.

Di fatto, ogni successione s₀s₁s₂... di 0 e di 1 (a eccezione di quelle successioni che terminano in una coda di 1) è l'itinerario di un certo punto x in I, e x è proprio il numero la cui rappresentazione binaria è s₀s₁s₂... Ne consegue che ciascun x in I ha uno e un solo itinerario.

Per comprendere le dinamiche della funzione di raddoppio, basta descrivere l'effetto del raddoppio sugli itinerari. In termini di successioni binarie, se x ∈ I, si può scrivere:

dove s₀s₁s₂... è l'itinerario di x. Il punto D (x) è espresso da:

perché D (x) = 2x mod1; ossia l'itinerario di D (x) si ricava dall'itinerario di x semplicemente eliminando la prima cifra. Similmente l'itinerario nell'n-esimo punto dell'orbita di x è semplicemente s_ns_n+1s_n+2...

Le conseguenze che ne derivano sono numerose. La prima è che, se x è un punto periodico per D, il suo itinerario deve essere una successione che si ripete; ed è vero anche l'inverso. Inoltre, è facile produrre un punto di partenza la cui orbita sia densa. A questo scopo basta determinare un punto di partenza la cui orbita sia arbitrariamente vicina a qualsiasi altra orbita in 0 ≤ x ≤ 1. Ecco l'itinerario di un'orbita siffatta:

Esso è composto da tutti i possibili blocchi di 0 e 1 con lunghezza n, per n = 1, 2, 3, ... L'orbita di questo punto ha un itinerario che deriva da quello originale semplicemente omettendo ripetutamente la prima cifra. Due itinerari sono vicini se le prime n caselle coincidono. Maggiore è il numero delle caselle comuni, più vicini sono i punti. Dunque l'orbita con l'itinerario prestabilito passa arbitrariamente vicino a qualsiasi punto dell'intervallo, come si vede facilmente eliminando un numero sufficiente di cifre iniziali, così che l'itinerario risultante coincide con lo sviluppo binario del dato punto nelle prime n caselle.

7. Il gioco del caos

Finora ci siamo limitati a studiare semplici iterazioni della retta. Per ampliare il tema di questo articolo e introdurre la nozione di frattale, passiamo a descrivere brevemente l'iterazione di sistemi di funzioni. L'esempio più semplice di una funzione iterata è il gioco del caos (v. Barnsley, 1988), che si svolge in questo modo: fissiamo nel piano tre punti, che chiameremo A, B e C, sui vertici di un triangolo. Scegliamo poi nel triangolo un altro punto che ci servirà come origine dell'iterazione e che chiameremo z₀ . Il punto successivo nell'orbita, z₁, sarà il punto di mezzo tra z₀ e uno dei vertici A, B, o C scelto a caso. Ripetiamo lo stesso procedimento prendendo z₂ nel punto di mezzo tra z₁ e un vertice scelto a caso. Nella fig. 14 si vede quali sono i risultati quando i vertici scelti sono A, A, B, C, C.

Ci si potrebbe aspettare che la successione di punti costruita mediante questa iterazione casuale abbia un andamento confuso. Invece, il risultato è tutt'altro che casuale, come indica la fig. 15, ove si sono tracciate 20.000 iterazioni (in realtà non abbiamo tracciato le prime 25 iterazioni ma soltanto gli ultimi 19.975 punti dell'orbita). Questa figura, nota in matematica come triangolo di Sierpinski, è un esempio di frattale. Un frattale è un oggetto localmente simile a se stesso la cui dimensione è strettamente superiore alla sua dimensione topologica (v. cap. 8). La dimensione frattale del triangolo di Sierpinski è log 3/log 2 ≅ 1,584..., mentre la sua dimensione topologica è 1, come vedremo tra poco. Il triangolo di Sierpinski è localmente simile a se stesso, come risulta osservando che è composto da tre copie, identiche ma più piccole, del triangolo, ciascuna delle quali, se raddoppiata, dà il triangolo originale, ma è costituito anche da 9 piccole copie di se stesso, ciascuna delle quali deve essere ingrandita con un fattore 4 per ottenere l'immagine originale.

Per comprendere come il gioco del caos crei il triangolo di Sierpinski, supponiamo di cominciare con il dato iniziale z₀ che si trova nel triangolo centrale, quello più grande all'interno della fig. 15. Indipendentemente dal vertice scelto, il punto z₁ si trova nel triangolo bianco appena più piccolo. Nell'iterazione successiva, z₂ viene a trovarsi nei triangoli bianchi immediatamente più piccoli, ecc. Pertanto l'orbita z₀, z₁, z₂, tende al confine dell'insieme di tutti i triangoli rimossi. Questo insieme, che è appunto il triangolo di Sierpinski, è l'attrattore per il gioco del caos. Con probabilità 1, tutte le orbite tendono, per iterazione, a diffondersi su tutto l'insieme. Dopo un numero assai limitato di iterazioni, l'orbita esce dalle aree bianche visibili e sembra avvicinarsi sempre di più all'attrattore.

Si osservi che la figura tracciata da questa orbita casuale non dipende dal dato scelto inizialmente, purché la scelta dei vertici A, B, C sia casuale. Se, per esempio, si sceglie sempre il vertice A (e questa non può certo definirsi una scelta casuale), il risultato sarà semplicemente una successione di punti tendenti al vertice A del triangolo di Sierpinski.

Molte variazioni sono possibili nel gioco del caos. Se per esempio si scelgono cinque punti nei vertici e al centro di un quadrato e si cambia da 2 a 3 il rapporto di compressione con il quale ci si muove verso i vertici (ossia si percorrono 2/3 della distanza verso il vertice prescelto o verso il centro), l'immagine che ne risulta è quella che compare nella fig. 16A. Se scegliamo sei punti ai vertici di un esagono regolare e usiamo un rapporto di compressione uguale a 3, l'immagine che se ne ricava è quella della fig. 16B.

Si osservi che ciascuna di queste figure è un oggetto localmente simile a se stesso. Questo fatto mette in rilievo una delle caratteristiche più sorprendenti del caos. Le dinamiche che entrano in gioco nel caso di immagini come quella del triangolo di Sierpinski sono incredibilmente complicate e caotiche. Tuttavia, dal punto di vista geometrico, esiste una regolarità in queste dinamiche, e l'attrattore è un esempio di frattale. Questo è un fatto tipico nella teoria dei sistemi dinamici. Quando si presenta il caos, quasi sempre il luogo dove si verifica è un frattale.

8. Frattali

Vogliamo chiarire meglio la definizione di frattale che abbiamo dato nel capitolo precedente. Ricordiamo che si dice frattale un oggetto localmente simile a se stesso e di dimensione eccedente la sua dimensione topologica. È opportuno perciò dare una spiegazione più completa del concetto di dimensione.

Esistono diversi tipi di dimensione in matematica, tra cui la dimensione di Hausdorff e la dimensione, familiare a tutti, per cui una retta ha dimensione 1, un piano dimensione 2, ecc. Qui ci occuperemo soltanto della dimensione frattale, perché è la più facile da spiegare. La dimensione topologica è sempre un numero intero: 0, 1, 2, ..., e si adatta alla nozione abituale di dimensione per oggetti geometrici semplici come le rette, i piani, le curve o le superfici. La dimensione frattale si usa per oggetti più complessi, localmente simili a se stessi come il triangolo di Sierpinski. Ora, oggetti semplici come un intervallo, un quadrato o un cubo, sono anch'essi localmente simili a se stessi e ciascuno di essi ha lunghezza uguale a 1/n della lunghezza originale. Si può esprimere questo concetto anche osservando che ciascuno degli n intervalli più piccoli, se ingrandito con un fattore n, dà l'immagine intera. Un quadrato può essere diviso in n² pezzi più piccoli, ciascuno dei quali può essere ingrandito con un fattore di ingrandimento n riproducendo così il quadrato originale. Il cubo è costituito da n³ pezzi simili a se stessi. Si osservi che, in ciascuno dei casi considerati, la dimensione è l'esponente del numero dei pezzi localmente simili a se stessi. Questa osservazione è alla base della seguente definizione di dimensione di frattale:

Per esempio, per il cubo si ha:

Come abbiamo visto precedentemente, il triangolo di Sierpinski può essere diviso in tre pezzi localmente simili a se stessi, ciascuno dei quali può essere ingrandito con un fattore 2 ottenendo la figura intera. Pertanto la sua dimensione frattale è:

Ma il triangolo di Sierpinski è costituito anche da 9 pezzi localmente simili a se stessi, ciascuno dei quali ha fattore di ingrandimento 4. Troviamo ancora la dimensione frattale:

Si osservi che la dimensione frattale coglie, in un certo senso, ciò che vedono i nostri occhi: il triangolo di Sierpinski è un oggetto più complicato di una curva a una dimensione, ma non riempie un piano a due dimensioni o una superficie. In accordo con ciò, la sua dimensione è compresa fra le due. Per completezza di informazione, la dimensione frattale dell'immagine nella fig. 16A è log 5/log 3, mentre quella nella fig. 16B è log 6/log 3.

I frattali nascono spesso come insiemi caotici per i sistemi dinamici, ma questo non è l'unico ambito in cui si possono produrre. È per esempio possibile ottenere il triangolo di Sierpinski mediante il seguente procedimento puramente deterministico. Prendiamo un triangolo ed eliminiamone ‛la parte centrale' in modo che rimangano soltanto tre triangoli, ciascuno dei quali sia esattamente la metà, in altezza, di quello originale. Iteriamo questo procedimento togliendo da ogni triangolo il centro e lasciando soltanto tre triangoli più piccoli come nella fig. 17. Il limite di questo processo è naturalmente il triangolo di Sierpinski.

Facciamo un altro esempio, partendo ancora da un triangolo. L'iterazione consiste nel rimuovere da ogni lato la parte centrale, uguale a un terzo dell'intero lato, e nel sostituirla con una coppia di segmenti di uguale lunghezza diretti verso l'esterno, nel modo indicato nella fig. 18. Il limite di questo procedimento è il ‛fiocco di neve di Koch'. Questa curva, a rigore, non è un frattale, perché ciascuna parte del fiocco di neve non è simile all'intero oggetto. Tuttavia ciascuno dei tre lati è un frattale (che si chiama curva di Koch; v. fig. 19) e ha dimensione frattale log 4/log 3 = = 1,261...

Il fiocco di neve di Koch, come molti altri frattali, gode di interessanti proprietà geometriche. Per esempio, l'area di un fiocco di neve è chiaramente finita, ma il perimetro della figura è infinito. Di fatto, a ogni passaggio nella costruzione di un fiocco di neve, il perimetro cresce per un fattore 4/3. All'n-esimo passaggio il perimetro è pertanto (4/3)ⁿ P₀, ove P₀ è il perimetro iniziale.

BIBLIOGRAFIA

Barnsley, M., Fractals everywhere, Boston 1988.

Bowen, R., On axiom A diffeomorphisms, Providence, R. I., 1978.

Devaney, R. L., Chaos, fractals and dynamics, Reading, Mass., 1990 (tr. it.: Caos e frattali, Milano 1990).

Feigenbaum, M., Quantitative universality for a class of nonlinear transformations, in ‟Journal of statistical physics", 1978, XXI, p. 669.

Lorenz, E. N., Deterministic nonperiodic flows, in ‟Journal of atmospheric sciences", 1963, XX, pp. 130-141.

Mandelbrot, B., The fractal geometry of nature, San Francisco 1982.

Poincaré, H., Sur les équations de la dynamique et le problème des trois corps, in ‟Acta mathematica", 1890, XIII, pp. 1-270.

Sarkovskii, A. N., Coexistence of cycles of a continuous map of a line into itself, in ‟Ukrainskii mathematicheskij žurnal", 1964, XVI, pp. 61-71.

Smale, S., Diffeomorphisms with many periodic points, in Differential and combinatorial topology; a symposium in honor of Marston Morse (a cura di S. S. Cairns), Princeton, N. J., 1965, pp. 63-80.