1 Introduction

Quantum entanglement is a strong type of non-classical correlations, making it the key to many applications in quantum computing and information [1]. Consequently, this becomes a pivotal component in advanced quantum information technologies, notably quantum sensing [2], quantum computation [3, 4], quantum cryptography [5, 6], quantum teleportation [7,8,9], quantum randomness [10], quantum dense coding [11], and so on. Many quantifiers were proposed to quantify the amount of quantum entanglement, such as entanglement of formation, negativity, concurrence, and logarithmic negativity [12,13,14,15,16,17,18,19,20,21,22,23,24]. In recent decades, numerous efforts have been undertaken to identify the most effective measure among various alternatives. However, it is difficult to say definitively that one measure is better than the others, as each one offers unique advantages depending on specific conditions. In this context, quantum entanglement has been extensively examined in many papers using different quantifiers [25,26,27,28,29,30].

The uncertainty principle, initially postulated by Heisenberg [31], lies at the heart of quantum mechanics, crucially illustrating the distinction between the quantum and classical worlds. Since then, Robertson [32] has expanded the concept of the uncertainty principle to encompass any two incompatible observables. Instead of using standard deviation and based on the concept of entropy, other interpretations of the uncertainty principle have been proposed [33,34,35,36]. In this sense, Berta and his colleagues [37] discovered that the uncertainty principle could be strengthened by taking into consideration an entangled quantum memory associated with the measured particle. Thereby, the concept of quantum-memory-assisted entropic uncertainty relation (QMA-EUR) is highly correlated with the connection of the particle to the quantum memory. Furthermore, it was found that the bound of QMA-EUR can be further refined by taking into account the quantum discord and the classical correlations associated with the measured particle [38]. The QMA-EUR has various potential applications, including probing quantum correlations [38, 39], entanglement witness [40, 41], quantum speed limit [42, 43], quantum cryptography [44], quantum metrology [45], and quantum key distribution [46]. Moreover, the QMA-EUR has been generalized and investigated in various bipartite and multipartite quantum systems [47,48,49,50,51,52,53,54]. In addition, EUR with and without quantum memory were derived for multiple measurements settings [55]. By taking into account the mutual information and the Holevo quantity, Xie et al. further tightened the lower bound of EUR for multiple measurements [56].

Exploring quantum entanglement, non-classical correlations, and QMA-EUR in Heisenberg spin-chain models, is attracting growing interest within the scientific community. Within this domain, numerous researchers have undertaken investigations into quantum resources and QMA-EUR in a variety of bipartite and multipartite quantum systems, including Heisenberg spin-chain models [46, 50, 57,58,59,60,61,62]. Additionally, there has been extensive scrutiny of the dynamics of quantum resources in a bipartite Heisenberg XXZ model under the influence of Dzyaloshinsky–Moriya (DM) interaction (referenced as [63,64,65]).

Apart from Heisenberg spin models, EUR and quantumness were investigated in other interesting systems at the intersection between quantum information and elementary particle physics or relativity theory, such as experimentally observed neutron oscillations [66,67,68] or Dirac fields in the background of Garfinkle–Horowitz–Strominger (GHS)—dilation black holes [69]. However, despite these extensive efforts, a significant gap remains unaddressed in the realm of quantum entanglement and QMA-EUR when considering the XXZ model in conjunction with Herring–Flicker coupling. Hence, it is crucial to spotlight the behaviors of quantum entanglement and QMA-EUR within this framework. In realistic settings, and due to quantum fluctuations, spins are not frozen on their lattice sites, thus it is an interesting prospect to assume that the coupling strength between spins might depend on the distance separating them. Indeed, the Herring–Flicker coupling relies on the inter-spin relative distance (R), offering an insight into its real essence within the Heisenberg XXZ model. Therefore, it is crucial to explore the impact of the distance R on the thermal entanglement and QMA-EUR in the bipartite Heisenberg XXZ model. Moreover, we aim to study the effects of the DM interaction and an external magnetic field on thermal entanglement while considering the distance R and other system parameters.

Building upon earlier research, specifically investigations into the effects of Herring–Flicker coupling [70, 71], our study delves into the fundamental relationship between bipartite entanglement and QMA-EUR in a two-qubit Heisenberg system with Herring–Flicker coupling. The main objective is to examine how the HF coupling distance affects various quantum indicators within this system in the presence of the Dzyaloshinskii-Moriya (DM) interaction and an external magnetic field. Within this context, Huang and Kais [72] have previously demonstrated the dependence of entanglement in an XY spin chain, governed by the Ising model, on the distance associated with Herring–Flicker coupling [73]. Notably, their research revealed that an increase in the magnetic field strength leads to a reduction in entanglement over the Herring–Flicker coupling distance. This coupling mechanism plays a crucial role in delineating the energy difference between the triplet and singlet states of the hydrogen molecule, as expounded in reference [73]. This difference is quantified as \(J(R) = E_\text {triplet} - E_\text {singlet} = 1.642~e^{-2R}R^{5/2}+O(R^{2}e^{-2R})\), which implies that the distinction between the symmetric and antisymmetric state energies must be exceedingly small, decaying exponentially as \(e^{-2R}\). Thus, by manipulating the coupling distance, the energy difference becomes adjustable. Building upon these findings, our paper delves into the study of correlations within a bipartite Heisenberg XXZ model. This model includes the Herring–Flicker coupling, the DM interaction, and the external uniform magnetic field. The Herring–Flicker approximation is a valuable tool for gauging the strength of the exchange interaction between the two qubits in the Heisenberg XXZ model. Here, we examine the impact of various factors, including the inter-spin relative distance R, the DM interaction, the anisotropy parameter, the external magnetic field, and the equilibrium temperature, on the variations in thermal entanglement and QMA-EUR within the Heisenberg model under consideration.

We structure our paper, as follows: In Sect. 2, we briefly introduce essential definitions and expressions related to logarithmic negativity (\(\mathcal{L}\mathcal{N}\)) and QMA-EUR. In Sect. 3, we outline the Hamiltonian for the bipartite Heisenberg XXZ model with Herring–Flicker coupling under DM interaction and derive the associated thermal density matrix using Gibbs equation. Section 4 presents and analyzes the behaviors of QMA-EUR and logarithmic negativity within the studied system. In Sect. 5, we summarize the main findings of our research.

2 Quantum indicators

We provide in this section the definitions of QMA-EUR and logarithmic negativity employed in this study to measure, respectively, the measurement uncertainty and the amount of entanglement between the two qubits in the considered system.

2.1 \(\mathcal{L}\mathcal{N}\)

\(\mathcal{L}\mathcal{N}\) is an extensively used measure of entanglement since it is easy to compute [20, 21]. Given a bipartite density matrix \(\rho\), \(\mathcal{L}\mathcal{N}\) is given as follows

$$\begin{aligned} \mathcal{L}\mathcal{N}(\rho )=\log _2\Vert \rho ^{T_2}\Vert _1, \end{aligned}$$
(1)

where the notation \(\Vert \rho ^{T_2}\Vert _1=Tr\big (\sqrt{\rho ^{T_2}(\rho ^{T_2})^{\dagger }}\big )\) is the trace norm of the partial transpose \({\rho ^{T_2}}\) [17, 23]. We resort to the following expression to compute the logarithmic negativity

$$\begin{aligned} \mathcal{L}\mathcal{N}(\rho )= \log _{2} \left( \sum _{j} |\kappa _j| \right) , \end{aligned}$$
(2)

where \(\kappa _j\) are the negative eigenvalues of \(\rho ^{T_2}\). \(\mathcal{L}\mathcal{N}\) varies from 0 to 1; it cancels out (\(\mathcal{L}\mathcal{N}(\rho )=0\)) for unentangled states and it is maximal (\(\mathcal{L}\mathcal{N}(\rho )=1\)) for bipartite states with maximal entanglement.

2.2 QMA-EUR

Uncertainty relations limit the potential information one can gather about a system’s physical properties. For two arbitrary observables \(\mathcal {O}\) and \(\mathcal {W}\), this uncertainty can be expressed using the standard deviation \(\Delta \mathcal {O}=\sqrt{\langle \mathcal {O}^{2}\rangle -\langle \mathcal {O}\rangle ^{2}}\) as [32]

$$\begin{aligned} \Delta \mathcal {O} \Delta \mathcal {W}\ge \dfrac{1}{2}\vert \langle [\mathcal {O},\mathcal {W}]\rangle \vert . \end{aligned}$$
(3)

However, in the framework of information theory, uncertainty relations are written in terms of the entropy. Among these entropic uncertainty relations, we find the following relation [36, 37] based on the Shannon entropy \(H(\mathcal {O})\):

$$\begin{aligned} H(\mathcal {O})+H(\mathcal {W})\ge log_{2}\dfrac{1}{c}, \end{aligned}$$
(4)

the term \(\dfrac{1}{c}\) quantifies the complementarity of the two observables, with \(c=\max _{kl}\vert \langle o_{k}\mid w_{l}\rangle \vert ^{2}\). \(\vert o_{k}\rangle\) and \(\vert w_{l}\rangle\) are, respectively, the eigenvectors of \(\mathcal {O}\) and \(\mathcal {W}\).

Uncertainty relations can be thought of by considering two parties; Alice and Bob who agree on two measurements \(\mathcal {O}\) and \(\mathcal {W}\). Bob creates a particle in a desired quantum state and transmits it to Alice, who then performs one of the two measurements and informs Bob of her decision. Bob has to reduce his uncertainty regarding the outcome of Alice’s measurement. Berta et al. [37] proved that in order to achieve his task and minimize the uncertainty, Bob should entangle the particle he sends to Alice to a quantum memory. This new improved uncertainty relation, named QMA-EUR is written in terms of the von Neumann entropy [37]

$$\begin{aligned} S(\mathcal {O}\vert B)+S(\mathcal {W}\vert B)\ge S(A\vert B)+ \log _{2}\dfrac{1}{c}, \end{aligned}$$
(5)

where the conditional von Neumann entropy \(S(\mathcal {O}(\mathcal {W})\vert B)=S(\rho _{\mathcal {O}(\mathcal {W})B})-S(\rho _{B})\) quantifies the uncertainty about the result of the measurement \(\mathcal {O}(\mathcal {W})\) given the information stored in the quantum memory B. \(\rho _{\mathcal {O}}=\sum _{k}(\vert o_{k}\rangle \langle o_{k}\vert \otimes I)\rho _{AB}(\vert o_{k}\rangle \langle o_{k}\vert \otimes I)\) and \(\rho _{\mathcal {W}}=\sum _{l}(\vert w_{l}\rangle \langle w_{l}\vert \otimes I)\rho _{AB}(\vert w_{l}\rangle \langle w_{l}\vert \otimes I)\) are the post-measurements states and \(\rho _{B}\) is the reduced density matrix describing the quantum memory B. Moreover, the supplementary term \(S(A\vert B)\) in the bound of the inequality (5) quantifies the amount of entanglement between the particles A and B. In this manuscript, we choose our two measurements to be the Pauli matrices \(\sigma _{x}\) and \(\sigma _z\). Therefore, we find that \(c=\frac{1}{2}\). The left-hand side of the inequality is the measured QMA-EUR, and it is given by

$$\begin{aligned} U_{L}=-2S(\rho _{B}) + S(\rho _{\sigma _{x}B})+S(\rho _{\sigma _{z}B}). \end{aligned}$$
(6)

The right-hand side of the inequality is the bound constricting the estimation accuracy by Bob. It is computed using the following expression

$$\begin{aligned} U_{R}=\log _{2}\dfrac{1}{c}+ S(\rho _{AB})-S(\rho _{B}). \end{aligned}$$
(7)

3 Setup

In this research, we investigate a system consisting of two spins described by a Heisenberg model. The system is subjected to the Dzyaloshinsky–Moriya interaction with a uniform external magnetic field B. The spins are assumed to be coupled through the Herring–Flicker interaction. The system’s Hamiltonian can be expressed as follows

$$\begin{aligned} H = J(R)\left( \sigma _{1}^{x}\sigma _{2}^{x} + \sigma _{1}^{y}\sigma _{2}^{y} + \delta \sigma _{1}^{z}\sigma _{2}^{z}\right) + {\vec{D}} .(\mathbf {{\vec{\sigma}} _{1} }\wedge \mathbf {{\vec{\sigma}} _{2}}) + B\left( \sigma _{1}^{z} + \sigma _{2}^{z}\right) , \end{aligned}$$
(8)

here, \(\sigma _{i=1,2}^{\alpha }\) (with \(\alpha =x,y,z\)) represent the Pauli matrices. The parameter \(\delta\) signifies the anisotropy factor, and \(\vec{D}\) denotes the Dzyaloshinsky–Moriya interaction vector, assumed to be oriented along the z-axis, that is: \(\textbf{D}.(\mathbf {\sigma _{1} }\wedge \mathbf {\sigma _{2}}) = {\vec{D}}_{z}\left( {\vec{\sigma}} _{1}^{x}{\vec{\sigma}} _{2}^{y} - \sigma _{1}^{y}\sigma _{2}^{x}\right)\). Furthermore, B represents the external magnetic field along the z-axis. The Herring–Flicker coupling J(R) that characterizes the interaction between the qubits is given by:

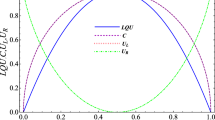
$$\begin{aligned} J(R)= \alpha _{HF}~ e^{-2R}R^{5/2}+O(R^{2}e^{-2R}), \end{aligned}$$
(9)

with the leading-order coefficient \(\alpha _{HF}=1.642\). The strength of the exchange interaction J(R), diminishes exponentially, and it is generally considered a short-range interaction. The accompanying figure provides a visual depiction of the coupling between two spins as a function of the relative distance R (Fig. 1);

Fig. 1
figure 1

Variation of J(R) versus the coupling distance R

Full size image

In the standard computational basis \(\{\lbrace \vert jk \rangle ; ~ j,k = 0,1 \}\), the Hamiltonian given by Eq. (8) can be expressed as

$$\begin{aligned} H = \left( \begin{array}{cccc} J(R)\delta +2B &{} 0 &{} 0 &{} 0 \\ 0 &{} -J(R)\delta &{} 2J(R) +2iD_z &{} 0 \\ 0 &{} 2J(R) -2iD_z &{} -J(R)\delta &{} 0 \\ 0 &{} 0 &{} 0 &{} J(R)\delta -2B \end{array}\right) . \end{aligned}$$
(10)

By performing a direct computation, we can ascertain the eigenvalues and associated eigenvectors of the Hamiltonian provided in Eq. (10)

$$\begin{aligned}&E_1=J(R)\delta + 2B,{} & {} |\varphi _{1} \rangle =|00 \rangle ,\end{aligned}$$
(11)
$$\begin{aligned}&E_2= -J(R)\delta -2\xi ,{} & {} |\varphi _{2}\rangle =\frac{1}{\sqrt{2}}\Big [\frac{J(R)+iD_{z}}{\xi }|01 \rangle +|10 \rangle \Big ],\end{aligned}$$
(12)
$$\begin{aligned}&E_3= -J(R)\delta +2\xi ,{} & {} |\varphi _{3}\rangle =\frac{1}{\sqrt{2}}\Big [\frac{-J(R)-iD_{z}}{\xi }|01 \rangle +|10 \rangle \Big ], \end{aligned}$$
(13)
$$\begin{aligned}&E_4= J(R)\delta - 2B,{} & {} |\varphi _{4}\rangle =|11 \rangle , \end{aligned}$$
(14)

where \(\xi =\sqrt{D_{z}^{2}+J^{2}(R)}\).

The following Gibbs density operator describes the system with the Herring–Flicker interaction. This system and a reservoir are in thermal equilibrium at a temperature T

$$\begin{aligned} \rho (T)=\frac{e^{-\beta H}}{\mathcal {Z}}, \end{aligned}$$
(15)

here, we define \(\beta\) as \(\frac{1}{k_{B}T}\), where \(k_{B}\) represents the Boltzmann constant, which we conveniently set to unity. The partition function, \(\mathcal {Z}\), is expressed as \(\mathcal {Z} = \text {Tr}(e^{-\beta H}) = \sum _{i=1}^{4} e^{-\beta E_{i}}\). The resulting thermal density matrix is expressed in the calculation base as follows

$$\begin{aligned} \rho (T) = \left( \begin{array}{cccc} \rho _{11} &{} 0 &{} 0 &{} 0 \\ 0 &{} \rho _{22} &{} \rho _{23} &{} 0 \\ 0 &{} \rho _{32} &{} \rho _{33} &{} 0 \\ 0 &{} 0 &{} 0 &{} \rho _{44} \end{array}\right) . \end{aligned}$$
(16)

The elements of the density matrix are expressed as

$$\begin{aligned} \begin{aligned} \rho _{11}&=\frac{e^{-\frac{J(R)\delta +2B}{T}}}{\mathcal {Z}},\\ \rho _{22}&=\rho _{33}=\frac{e^{\frac{J(R)\delta }{T}}\cosh (\frac{2\xi }{T})}{\mathcal {Z}},\\ \rho _{44}&=\frac{e^{\frac{-J(R)\delta +2B}{T}}}{\mathcal {Z}},\\ \rho _{23}&=-\frac{e^{\frac{J(R)\delta }{T}}\frac{J(R)+iD_{z}}{\xi }\sinh (\frac{2\xi }{T})}{\mathcal {Z}},\\ \rho _{32}&=\rho ^{*}_{23}, \end{aligned} \end{aligned}$$
(17)

with the partition function \(\mathcal {Z}=2e^{-\frac{J(R)\delta }{T}}\Big (\cosh (\frac{2B}{T})+e^{\frac{2J(R)\delta }{T}}\cosh (\frac{2\xi }{T})\Big )\).

4 Discussion and results

Here, we highlight the results of our research, wherein we analyze the behavior of quantum entanglement measured via \(\mathcal{L}\mathcal{N}(\rho )\) and QMA-EUR within a two-qubit Heisenberg model featuring Herring–Flicker coupling under the impact of Dzyaloshinsky–Moriya interaction. We perform an in-depth examination of how various critical parameters, including the inter-spins relative distance (R), the external magnetic field (B), the equilibrium temperature (T), the strength of DM interaction (\(D_z\)), and the anisotropy parameter (\(\delta\)), impact the quantum metrics utilized in our study.

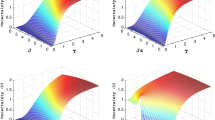
To initiate this exploration, Fig. 2 examines the impact of varying the coupling distance (R) on the QMA-EUR and thermal entanglement within the system under investigation. It is worth noting that all other system parameters are held constant, with values set to \(\delta =D_z=B=0.5\).

Fig. 2
figure 2

\(\mathcal{L}\mathcal{N}(\rho )\) (a–d) and QMA-EUR (b–c–e) in terms of T and R when \(\delta =D_z=B=0.5\)

Full size image

From Fig. 2a, d, it is worth remarking that the coupling distance R, and consequently the HF-coupling J(R) influence the behavior of thermal entanglement. In this light, we notice that two intervals of R values are distinguished; for \(0<R<1.25\), an improvement of \(\mathcal{L}\mathcal{N}(\rho )\) is observed. \(R=1.25\), which corresponds to the maximum of Herring–Flicker coupling \(J(R)\approx 0.2354\), is the ideal configuration of this parameter, allowing for a maximal strengthening of entanglement. Beyond this optimal coupling distance (\(R=1.25\)), \(\mathcal{L}\mathcal{N}(\rho )\) decreases and freezes into a constant value. It is clear from Fig. 2a, d that the effect of the temperature T is the most prevailing, such that entanglement decreases steadily and vanishes for growing T degrees. In Fig. 2d we recognize the phenomenon of entanglement sudden death (ESD) happening at specific critical temperatures \(T_c\). The values of \(T_c\) where the quantum phase transition entanglement-separability occurs, is improved for growing R in the range of \(0<R\le 1.25\). Thereby, we find that \(T_c(R=0.5)\approx 1.244\), while \(T_c(R=1.25)\approx 1.435\). In order to explain the entanglement sudden death behavior, we thoroughly investigate the expression of \(\mathcal{L}\mathcal{N}\) used to quantify entanglement. The density matrix \(\rho (T)\) (Eq. (16)) is an X state, so is its partial transpose \(\rho ^{T_B}(T)\). Further, we find that the eigenvalues of this latter are \(\kappa _1=\kappa _2=\rho _{22}\), which is a positive real. The other two eigenvalues are \(\kappa _{3,4}=\dfrac{(\rho _{11}+\rho _{44})\mp \sqrt{(\rho _{11}-\rho _{44})^{2}+4\vert \rho _{23} \vert ^{2}}}{2}\), we can clearly see that \(\kappa _4\) is always positive, which leaves us with \(\kappa _3\). In this specific chosen configuration of \(\delta =D_z=B=0.5\), we find that \(\kappa _3\) is negative for low T degrees, but as T grows, \(\kappa _3\) increases until reaching \(\kappa _3=0\) for a specific T, which depends on the relative distance R between the two spins. This specific temperature is the ESD temperature \(T_c\). The findings shown in Fig. 2a imply that higher strengths of the Herring–Flicker coupling between the two qubits can enhance thermal entanglement in the system under consideration at lower temperatures. This means that by regulating the system parameters and the Herring–Flicker coupling, we can somewhat shield our system against the negative impact of temperature on its quantum features, namely the amount of thermal entanglement captured here by \(\mathcal{L}\mathcal{N}(\rho )\). Moving on to Fig. 2b, c, e, where we observe that QMA-EUR displays the opposite behavior to that of thermal entanglement for different values of the coupling distance R. At lower temperatures, we observe that QMA-EUR reveals significant values for \(R=0\); i.e. in the absence of Herring–Flicker coupling. Whereas, as \(T=0\), the QMA-EUR is zero for all non-zero values of the coupling distance R. This finding indicates that introducing Herring–Flicker coupling can reduce QMA-EUR in the system at lower temperatures. As the temperature increases, QMA-EUR increases monotonically and reaches its maximal value (\(U_L=U_R\rightarrow 2\)) at higher temperatures. Consequently, by adequately adjusting the coupling distance R yielding higher Herring–Flicker coupling strength and by carefully selecting the other system parameters, it is possible to attenuate the harmful effects of temperature, reduce the QMA-EUR, and stabilize the amount of thermal entanglement within the investigated system.

Next, we present in Fig. 3, the impact of the DM interaction and the Herring–Flicker coupling distance on thermal entanglement and QMA-EUR in the two-qubit spin system. We fixed the remaining parameters at \(T=0.2\) and \(\delta =B=0.5\).

Fig. 3
figure 3

\(\mathcal{L}\mathcal{N}(\rho )\) (a–d) and QMA-EUR (b, c–e) in terms of R and \(D_z\) when \(T=0.2\) and \(\delta =B=0.5\)

Full size image

In Fig. 3a, d, a clear pattern emerges: when the DM interaction within the system is absent (\(D_z=0\)), \(\mathcal{L}\mathcal{N}(\rho )\) becomes nonexistent. A minor, insignificant level of thermal entanglement appears at a coupling distance of \(R=1.25\), which corresponds to the peak strength of the Herring–Flicker coupling, approximately \(J(R)\approx 0.2354\). Conversely, when the DM interaction becomes sufficiently strong (\(D_z\ge 2\)), the two spins become maximally entangled regardless of the coupling distance R between them. For small non-zero values of \(D_z\), it is observed that \(\mathcal{L}\mathcal{N}(\rho )\) initially increases, reaching its maximum at \(R=1.25\), and then decreases to stabilize at its initial value recorded for \(R=0\). These findings underscore the ability to optimize thermal entanglement within the system by fine-tuning both the Herring–Flicker coupling and the DM interaction. In Fig. 3b, c, and e, a notable contrast emerges in the behavior of QMA-EUR compared to thermal entanglement. Regardless of the coupling distance R, it becomes apparent that QMA-EUR diminishes as \(D_z\) increases and ultimately becomes negligible for higher levels of DM interaction strength. In fact, with high values of \(D_z\), there is a complete lack of uncertainty in the results of both measurements, \(\sigma _x\) and \(\sigma _z\), as reflected in the conditional entropies within the QMA-EUR: \(S(\rho _{\sigma _{x}B})-S(\rho _{B})=S(\rho _{\sigma _{z}B})-S(\rho _{B})=0\). Furthermore, in the lower bound \(U_R\), the term quantifying entanglement between the two qubits yields \(S(A\vert B)=-\log _2(d=2)=-1\), with d representing the dimension of the qubit A sent to Alice. Consequently, this indicates that the lower bound is also reduced to zero. These findings provide valuable insights into the interplay between thermal entanglement and the system’s parameters. Specifically, they shed light on the fact that thermal entanglement between the two qubits exhibits a notable enhancement within a defined range of distance values. This enhancement is closely related to the augmentation in the HF coupling J(R) and the presence of a substantial DM interaction. Furthermore, these observations emphasize an intriguing inverse relationship. As thermal entanglement becomes more pronounced and robust, the measure of QMA-EUR experiences a decline. This phenomenon implies a fine-tuned relationship between the level of quantum entanglement and the precision of measurements within the system. A rise in one factor corresponds to a decrease in the other. This connection can be explained theoretically by delving into quantum entanglement’s nature as a type of quantum correlation. Essentially, stronger quantum correlations result in a decrease in measurement uncertainty. In simpler terms, higher entanglement leads to less uncertainty, while lower uncertainty is associated with increased entanglement.

In Fig. 4, we illustrate the variations of thermal entanglement, \(U_L\), and \(U_R\) in the system under consideration as a function of Herring–Flicker coupling distance (R) for different given values of (B). The other defining parameters are set to \(T=0.2\) and \(\delta =D_z=0.5\).

Fig. 4
figure 4

\(\mathcal{L}\mathcal{N}(\rho )\) (a–d) and QMA-EUR (b–c–e) in terms of R and B when \(T=0.2\) and \(\delta =D_z=0.5\)

Full size image

Figure 4a–e offer a comprehensive view of how the interplay between the coupling distance R and the external magnetic field B affects the system. Figure 4a clearly illustrates that a strong magnetic field B causes quantum entanglement to vanish, regardless of the specific value of the coupling distance R. Meanwhile, in a scenario where the temperature remains fixed at \(T=0.2\), the quantifier \(\mathcal{L}\mathcal{N}(\rho )\) approaches its maximum value of 1 when \(B=0\), regardless of the chosen value for R. Moreover, when \(B=0.5\), we observe a noteworthy trend in \(\mathcal{L}\mathcal{N}(\rho )\) as it increases with the growing value of R until reaching its peak at \(R=1.25\). This particular coupling distance corresponds to the point where the HF coupling achieves its maximum value. Subsequently, \(\mathcal{L}\mathcal{N}(\rho )\) gradually decreases and stabilizes at its initial value, which is approximately \(\mathcal{L}\mathcal{N}(\rho )\approx 0.26\), as the coupling distance R continues to increase. This trend underscores that the coupling distance between the two qubits enhances thermal entanglement within the examined system, specifically at \(R=1.25\). In contrast, Fig. 4b, c clearly demonstrate that the absence of B leads to a reduction in both \(U_L\) and \(U_R\) within the system. As the magnetic field strength, B, increases, both \(U_L\) and \(U_R\) reach their respective peaks but eventually stabilize at a consistent value of (\(U_L=U_R=1\)) at higher B values. In contrast, the behavior depicted in Fig. 4e reveals that QMA-EUR experiences a decrease in the absence of an external magnetic field (\(B=0\)). Remarkably, it is even possible to entirely eliminate measurement uncertainty when \(R=1.25\), as we find that both \(U_L\) and \(U_R\) reach a value of zero. As the external magnetic field B is introduced into the system, QMA-EUR attains its highest value, after which, with an increase in the coupling distance R, this value gradually diminishes, reaching its minimum value at \(R=1.25\). Subsequently, it rises again to reach a stable value at higher values of the coupling distance R. Moreover, at elevated levels of the magnetic field (\(B=3\)), it becomes evident that QMA-EUR remains constant, with both \(U_L\) and \(U_R\) equal to one, regardless of the specific coupling distance R.

Now, let us investigate in Fig. 5 the impact of DM interaction \((D_z)\) on the variation of our quantum indicators when \(R=1.5\) and \(\delta =B=0.5\).

Fig. 5
figure 5

\(\mathcal{L}\mathcal{N}(\rho )\) (a) and QMA-EUR (b) as a function of T for different values of \(D_z\) when \(R=1.5\) and \(\delta =B=0.5\)

Full size image

In Fig. 5a, it is evident that the strength of the DM interaction \(D_z\) plays a crucial role in mitigating the adverse effects of rising temperatures (T). When there is no DM interaction (\(D_z=0\)), it is clear that \(\mathcal{L}\mathcal{N}(\rho )\) becomes null (\(\mathcal{L}\mathcal{N}(\rho )=0\)) for all temperatures, except for a slight peak occurring at nearly zero temperatures. However, with non-zero \(D_z\) values, \(\mathcal{L}\mathcal{N}(\rho )\) distinctly captures maximum thermal entanglement at lower temperatures (\(T\rightarrow 0\)). This entanglement gradually diminishes as temperature increases and drops to zero at critical temperatures (\(T_c\)), which are dependent on the values of \(D_z\). Remarkably, higher DM interaction strengths allow for the maintenance of maximal entanglement even at relatively high temperatures. This is reflected in the width of the plateau regions presented in Fig. 5a. Furthermore, an increase in \(D_z\) results in raising the critical temperature at which the entangled state is lost. In Fig. 5b, it becomes clear that the amount of QMA-EUR in the system at low temperatures (\(T\rightarrow 0\)) is dependent on the strength of the DM interaction. For \(D_z\ne 0\), both \(U_L\) and \(U_R\) reach a value of zero, corresponding to a maximally entangled state. Conversely, in the absence of the DM interaction (\(D_z=0\)), we find that \(U_L=U_R=1\). As temperature increases, QMA-EUR rises and eventually stabilizes at a value of \(U_L=2\) at higher temperatures. To summarize, the relationship between QMA-EUR and quantum entanglement within the system offers valuable insights. These two indicators display contrasting behaviors in response to the various parameters defining the Heisenberg model under investigation. By analyzing the dynamics of quantum entanglement, one can effectively anticipate the corresponding changes in QMA-EUR, and conversely, observing the fluctuations in QMA-EUR provides crucial insights into the evolving entanglement within the system. This reciprocal interaction between the two metrics sheds light on the intricate interplay of factors influencing the behavior of the studied system.

Next, we investigate in Fig. 6 the joint effect of \(\delta\) (the anisotropy parameter) on the variation of thermal entanglement and QMA-EUR within the considered Heisenberg system. The other system parameters are fixed at \(R=1.25\), \(B=0.2\), and \(D_z=3\).

Fig. 6
figure 6

\(\mathcal{L}\mathcal{N}(\rho )\) (a) and QMA-EUR (b) in terms of T for various values of \(\delta\) when \(R=1.25\), \(B=0.2\) and \(D_z=3\)

Full size image

In Fig. 6a, it is evident that \(\mathcal{L}\mathcal{N}(\rho )\) exhibits a significant amount of thermal entanglement at lower temperatures (\(T\rightarrow 0\)) across all values of \(\delta\). As the temperature T increases, the thermal entanglement within the two-qubit system decreases. This decrease indicates a transition from a maximally entangled state to an entangled state, where \(0<\mathcal{L}\mathcal{N}(\rho )<1\). At elevated temperatures, \(\mathcal{L}\mathcal{N}(\rho )\) declines rapidly and eventually reaches zero at a critical temperature (\(T_c\)), which is contingent upon the anisotropy parameter. For instance, when \(\delta =0\), the critical temperature is approximately \(T_c\approx 6.83\), while for \(\delta =2\), it is approximately \(T_c\approx 7.58\). At \(T_c\), the system assumes a separable state (\(\mathcal{L}\mathcal{N}(\rho )=0\)). Moreover, Fig. 6a highlights the role of the anisotropy parameter in enhancing thermal entanglement within the system. It is evident that the width of the plateau region in \(\mathcal{L}\mathcal{N}(\rho )\) slightly increases with higher \(\delta\). However, it is DM interaction that effectively preserves maximal entanglement with respect to temperature T (Fig. 5). In Fig. 6b, there is a clear inverse relationship between QMA-EUR and thermal entanglement. At low temperatures, QMA-EUR is consistently zero (\(U_L=U_R=0\)), but as the temperature rises, QMA-EUR increases steadily to reach a maximum value for all values of \(\delta\).

Finally, we examine how the external homogeneous magnetic field (B) impacts thermal entanglement and QMA-EUR within the considered system. To do this, we plot \(\mathcal{L}\mathcal{N}(\rho )\) and QMA-EUR in terms of temperature T for various values of B, and we set the other system parameters to \(R=1.5\) and \(\delta =D_z=0.5\), as shown in Fig. 7.

Fig. 7
figure 7

\(\mathcal{L}\mathcal{N}(\rho )\) (a) and QMA-EUR (b) in terms of T for various values of B when \(R=1.5\) and \(\delta =D_z=0.5\)

Full size image

Figure 7a provides valuable insights into the behavior of \(\mathcal{L}\mathcal{N}(\rho )\) in the absence of an external magnetic field (B). It is evident that \(\mathcal{L}\mathcal{N}(\rho )\) captures the maximum thermal entanglement in the ground state (\(T\rightarrow 0\)). As the temperature (T) increases, \(\mathcal{L}\mathcal{N}(\rho )\) declines rapidly and reaches zero at the critical temperature (\(T_c \approx 1.418\)). Importantly, the \(T_c\) value at which the quantum phase transition from entanglement to separability occurs is determined by the \(D_z\) value and remains independent of the magnetic field’s intensity (B). Additionally, the width of the plateau region decreases with increasing B. For \(B=1,\) a small resurgence of \(\mathcal{L}\mathcal{N}(\rho )\) is noticed around \(T\approx 0.2,\) but it eventually vanishes at \(T_c.\) Beyond a certain threshold of B, the two-qubit Heisenberg model becomes separable even at extremely low temperatures. This implies that the presence of B with higher intensities has a negative impact on the amount of thermal entanglement, as reflected in \(\mathcal{L}\mathcal{N}(\rho )\). Analyzing Fig. 7b, we can clearly observe that QMA-EUR exhibits a consistent increase with rising temperature (T), and throughout this progression, \(U_L\) remains consistently greater than \(U_R\). However, a noteworthy phenomenon occurs at the critical temperature (\(T_c\)), where thermal entanglement completely vanishes. At this point, QMA-EUR tends to stabilize at its maximum value, aligning perfectly with its lower bound, holding \(U_L=U_R=2\). Moreover, Fig. 7b highlights that the presence of an external magnetic field (B) enhances the QMA-EUR between the qubits in the studied system. Consequently, for low values of B (\(B\rightarrow 0\)), QMA-EUR commences at \(U_L=U_R=0\) when \(T=0,\) and then steadily increases as temperature rises. On the other hand, for higher values of B, it initiates at a substantial value (\(U_L=U_R=1\)). Overall, Fig. 7 underscores the strong connection between measurement uncertainty and the level of entanglement between the two qubits. It becomes evident that maximizing entanglement leads to the complete reduction of QMA-EUR, emphasizing the intricate interplay between these two key aspects in the system.

5 Conclusion

In summary, we have examined the relations and variations of thermal entanglement and quantum-memory-assisted entropic uncertainty (QMA-EUR) in a two-qubit one-dimensional XXZ Heisenberg spin-1/2 chain with Herring–Flicker coupling under an external homogeneous magnetic field and DM interaction at thermal equilibrium with a reservoir. Specifically, we examined the impact of Herring–Flicker coupling on thermal entanglement and QMA-EUR. It has been shown that Herring–Flicker coupling can enhance thermal entanglement against the negative impact of T and external magnetic field, specifically for the distance \(R=1.25\), which yields the maximal strength of the Herring–Flicker interaction. Our findings also demonstrate that increasing the anisotropy parameter and DM interaction strength can improve thermal entanglement in the system. Therefore, thermal entanglement between the two qubits is achieved and can be maintained by reducing the temperature and the intensities of the external magnetic field while simultaneously increasing the DM interaction and the anisotropy parameter. On the other hand, our results revealed that equilibrium temperature has a significant influence on QMA-EUR and that the latter shows marked variations according to this parameter. QMA-EUR grows for rising temperatures, reaching a steady maximum value (\(U_L=U_R=2\)) at greater temperature degrees. Moreover, our analysis shows that a strong Herring–Flicker coupling can lead to a reduction in QMA-EUR, and inversely, a strong external magnetic field may lead to the expansion of QMA-EUR. It is worth mentioning that although the graphical results obtained show unequivocally that quantum entanglement and QMA-EUR have an anti-correlated relationship, demonstrating that it is possible to reduce or even eliminate measurement uncertainty by achieving and preserving maximal amounts of entanglement in quantum systems, finding an analytical expression linking directly QMA-EUR or its lower bound \(U_R\) to \(\mathcal{L}\mathcal{N}(\rho )\) for any arbitrary X-state is a difficult task. Finally, this research provides valuable insights into optimizing a two-qubit XXZ Heisenberg model with Herring–Flicker coupling to achieve quantum advantages in quantum information processing.