Seven Bridges of Königsberg: How an ‘unsolvable’ puzzle shaped modern mathematics

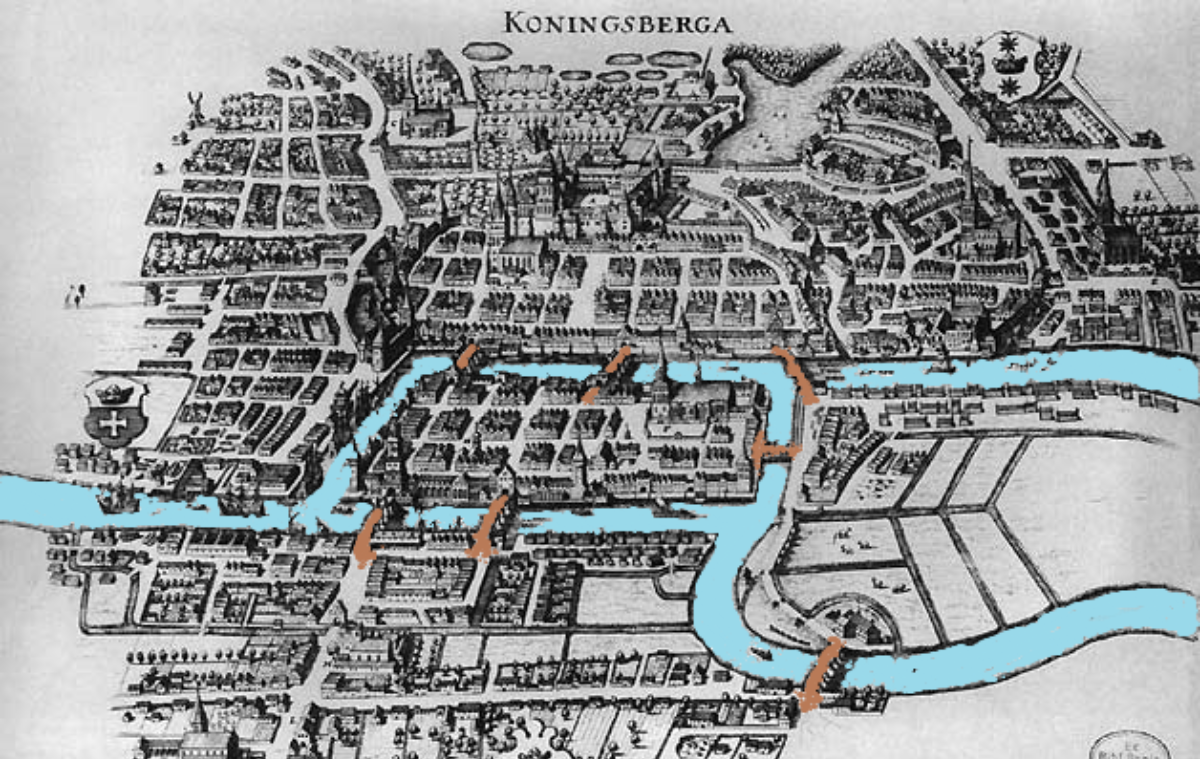Map of Königsberg, Prussia with its seven bridges in the 18th century.

Puzzled locals and authorities made several attempts to solve the problem, all futile. As frustration mounted over the years, Carl Leonhard Gottlieb Ehler, the mayor of Danzig, decided to write a letter to the mathematician Euler (yes, the same guy in your high-school textbooks, pronounced as ‘oiler’), requesting a solution. At first, Euler would consider the idea too trivial to fall under the purview of mathematics. However, he was also amused by the fact that there was no existing subfield of math that dealt with such problems. So he got to work, and started by simplifying the geography, representing the landmasses as vertices and the bridges as edges, as shown here:

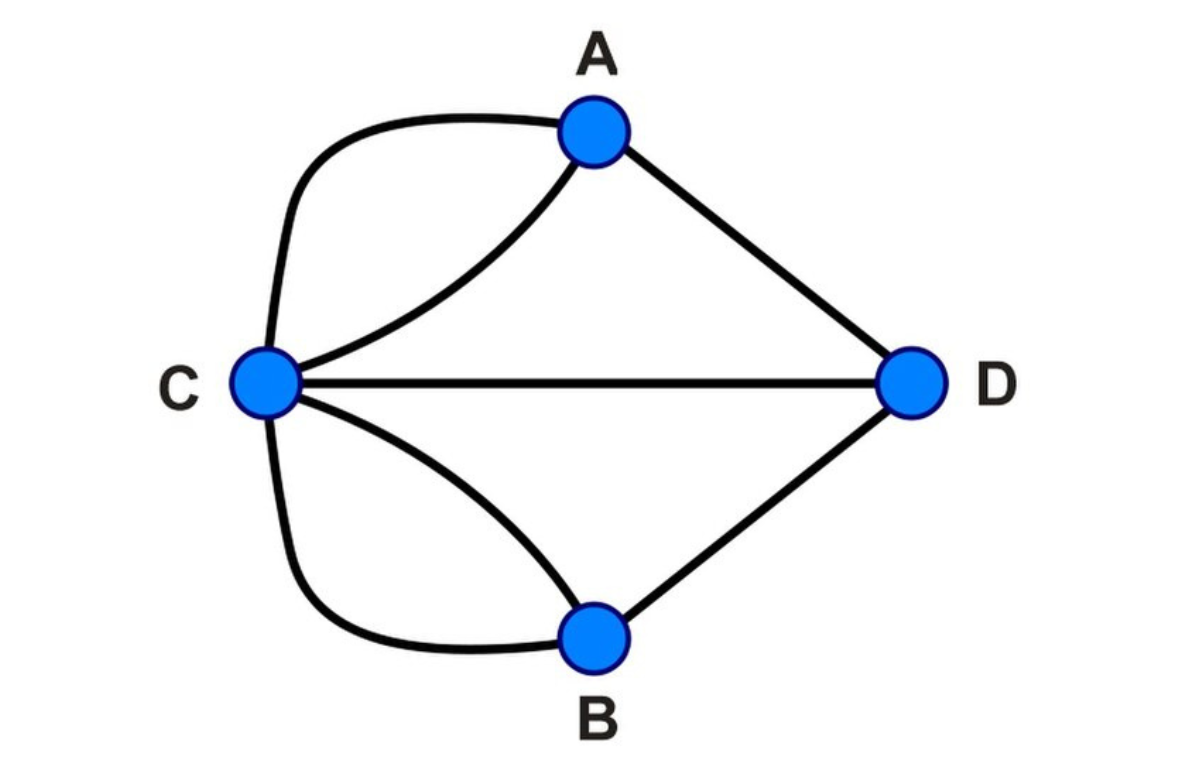How Euler simplified the map of Königsberg. (Diagram by Dafnell/Wikimedia Commons)

Seems rather simple right? The landmasses are represented by nodes with letters assigned to them, and the bridges simply connect the nodes together. Euler had abstracted the dilemma into a mathematical construct—a graph.

Now as for the solution, Euler saw that the number of lines connected to each vertice (or landmass) mattered. If a landmass had an odd number of lines connected to it, it meant you couldn’t walk around and cross each bridge exactly once. Since every landmass in Königsberg had an odd number of bridges connected to it, Euler concluded that the problem had a negative resolution — it couldn’t be solved. For citizens to avoid crossing the same bridge twice, one of the bridges would have to be erased. History delivered a devastating resolution here: in 1944, two of the original seven bridges were destroyed in the bombing of Königsberg during the Second World War.

The subtraction of two bridges meant that now, only one out of the four landmasses had an odd number of bridges connected to them, which theoretically allowed an Eulerian path that would form a smooth solution in the following manner:

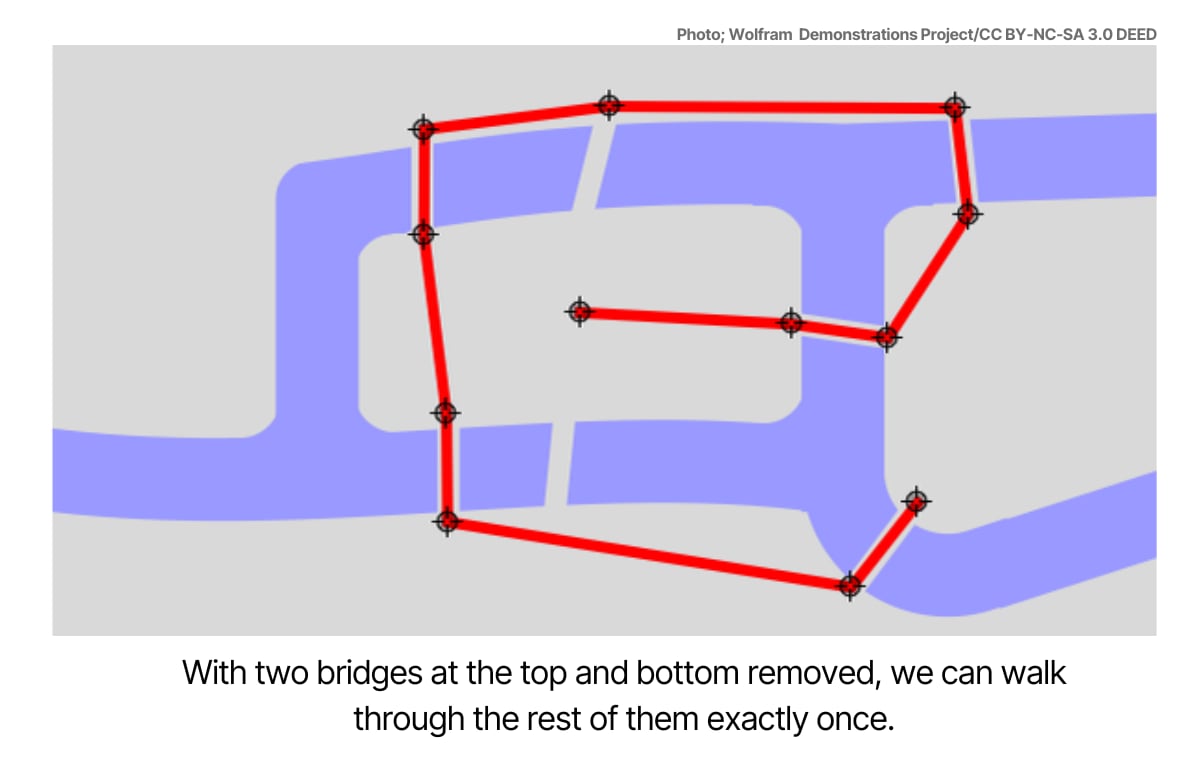Euler’s proposed resolution, which would remain theoretical.

How did Königsberg’s puzzle lead to new kinds of math?

Euler’s attempts to crack this urban planning problem laid the foundation for graph theory, a field dedicated to the study of networks comprised of interconnected nodes and edges. Graph theory deals with the planning of systems, exploring concepts like paths, cycles, and connectivity. From social media networks to finding navigable routes on Google Maps, to our brain’s neurons, this encompasses connections of all sorts. It’s closely intertwined with combinatorics, another mathematical discipline focusing on the counting and arrangement of distinct objects. Combinatorics deals with questions like “how many ways can items be arranged?” or “how many combinations are possible?” Sounds familiar? These same principles govern your daily games of sudoku!

Combinatorial principles are applied to determine feasible combinations within a puzzle’s constraints, while graph theory concepts can be used to analyze the relationships between cells in a sudoku grid, helping with big picture thinking to find the solution. Pro solvers, who do competitive sudoku, are in the habit of such quick strategic thinking.

While attempting to solve Königsberg’s conundrum, Euler also described it as a problem concerning ‘geometry of position’ – the shape of the land didn’t matter; it was how things were connected that was important. This idea and Euler’s later work would form the basics of a new area of math called topology.

A classic example of topology, also seen in ‘Everything Everywhere All at Once’ (2022).

Imagine you have a shape, like a donut or a cup. According to the principles of topology, they are the same because you can smoothly change one into the other without cutting or breaking them. It doesn’t matter if you stretch, twist, or bend the shape, as long as you don’t tear or glue any parts together. Simply put, it’s all about the core properties that don’t change despite external pressures, which is why topology is often called ‘rubber-sheet geometry’. A notable use of topology is in the study of spacetime, found in Einstein’s general theory of relativity.

Later mathematicians like Augustin-Louis Cauchy and Antoine Jean L’Huilier would come to build upon Euler’s ideas. For his unmatched influence on STEM, French polymath Pierre-Simon Laplace referred to Euler as “the master of us all”.

Both graph theory and topology are dominant fields of mathematics today, inspiring research and practical applications in computer science, network optimization, supply chain management, urban planning, internet routing and biology. In an intriguing experiment of graph theory, Japanese researchers got a slime mold—nicknamed ‘The Blob’—to almost accurately recreate the subway system of Tokyo.

One of numerous historical math problems

The seven bridges of Königsberg wasn’t the only puzzle that opened the gates for mathematical innovations. Many more have ignited thinkers across history — the Basel problem, which helped advance number theory, is another that was solved by Euler. For something similar to Königsberg, one may also look at the Knight’s Tour problem in chess. This is an instance of a graph theory concept called ‘Hamiltonian paths’, where the task is to find a sequence that allows a knight to travel all the squares of a chessboard exactly once. Interestingly, its origins lie in a 9th-century Sanskrit text called the ‘Kavyalankara’, composed by Kashmiri poet Rudrata. The problem was eventually solved using computer algorithms and heuristics (mental shortcuts).

Those going down the rabbit hole of unsolved problems will also encounter The Millenium Prize: an award given for solving seven of math’s greatest mysteries. Each offers a prize of one million dollars, if you can submit a valid proof. Offered by the Clay Mathematics Institute (CMI) in 2000, it includes problems like the Riemann Hypothesis, Yang-Mills theory, and the Navier-Stokes equation. Only one out of the seven Millennium problems has been solved so far: the Poincare conjecture, proven by Russian mathematician Grigori Perelman in 2003. Perelman famously rebuffed the CMI’s ways, publishing his proof online instead of on a peer-reviewed journal, and refusing to accept the sizeable prize money.

The ‘Three-Body Problem’, which you might know from Netflix these days, is another age-old enigma that has evaded scientists — an astronomical problem that deals with predicting the motion of three planetary bodies or masses under their gravitational interactions. It has no known solution yet, and to spice things up, any resulting systems created for this situation end up in pure chaos.

Curiosity didn’t kill the cat, it invented new math

The spirit of inquiry to solve the bridge problem—whether it was in the citizens of Königsberg, or Swiss genius Euler— offers an essential lesson about the rewards of trial and error when trying to overcome an ‘unsolvable’ problem. Even if a solution isn’t in sight, the simple habit of finding connections is known to compound over time and sharpen one’s eye for strategy, improve concentration, or unintentionally spark new ideas. We’re reaping the benefits of such habits in the form of graph theory and topology today. Who knows what tomorrow may bring?