El pasado mes de mayo de 2014, durante el evento que sirvió como celebración del 50 aniversario de los estudios de Matemáticas en la Universidad de Granada, Juan Medina (uno de los integrantes de la mesa sobre Matemáticas y Redes Sociales que tuve el honor de moderar) habló durante su intervención (por cierto, aquí tenéis la presentación que usó) sobre algunas de las cuestiones que le motivaron a crear su plataforma de vídeos. Entre ellas en mi mente quedó concretamente una, que me pareció bastante interesante y que es la que titula este post: ¿qué es un radián? Juan la citaba en el contexto de que los alumnos aprenden a hacer los ejercicios «tipo» y memorizan ciertas cuestiones (como el tema de los radianes), pero tienen carencias al manejar los propios conceptos (de hecho en ocasiones ni los conocen).
Como esa cuestión concreta se me quedó grabada, y aunque es muy probable que muchos de vosotros sepáis la respuesta, creo que puede interesar hablar un poco sobre él, sobre el radián.
El radián, al igual que el grado sexagesimal, es una unidad de medida de ángulos (de hecho es la medida de ángulo plano del Sistema Internacional de Medidas (como podéis comprobar en la página 118 de este pdf). Es decir, igual que podemos medir longitudes con metros o masas con gramos también podemos medir ángulos con radianes, expresándolo en ese caso con rad o sin nada. Por cierto, la aparición del radián data del último tercio del siglo XIX, y parece que el primero que lo utilizó fue James Thompson, ingeniero y físico hermano de Lord Kelvin. (Fuente: Earliest Known Uses of Some of the Words of Mathematics.)
Pero volvamos a hacernos la pregunta principal de esta entrada: ¿qué es exactamente un radián? Aquí tenéis su definición:
Un radián es el ángulo central de una circunferencia que abarca un arco de igual longitud que el radio de la misma.
Es decir, si nuestra circunferencia tiene radio , un radián es el ángulo que abarca un arco de longitud
:

Bien, ya que sabemos qué es un radián vamos a relacionarlo con la otra unidad de medida de ángulos que conocemos: el grado sexagesimal (o simplemente grado). La equivalencia entre estas dos medidas es la siguiente:
Por tanto, un radián corresponde a, aproximadamente, .
Siguiendo con esto, ¿qué pinta aquí, de nuevo, el número ? Veamos. En general, la medida en radianes de un ángulo en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia:
Si tomamos una semicircunferencia, cuya longitud es (como todos deberíamos saber), entonces tenemos lo siguiente:
Como sabemos que una semicircunferencia corresponde a un ángulo de ya tenemos nuestra relación:
.
Por tanto, a una circunferencia completa, que sabemos que abarca , le corresponden
radianes. Esto es evidente a partir de lo comentado anteriormente, aunque es mucho más mejor verlo en este delicioso gif que encontré aquí (donde, por cierto, aparecen más gifs interesantes sobre matemáticas):

Seguimos con más preguntas: ¿por qué cuando usamos funciones trigonométricas en cálculo solemos trabajar con radianes? Pues muy sencillo: porque las expresiones de muchos resultados quedan mucho mejor si trabajamos en radianes. Como dicen en la página de la Wikipedia en inglés dedicada al radián:
Los radianes poseen una «naturalidad» matemática que lleva a una formulación más elegante de unos cuantos resultados importantes.
Por ejemplo, si expresamos en radianes conservamos este bonito límite:
O también la preciosidad de serie de Taylor a la que es igual la propia función :
Bueno, pues ya sabemos lo que es un radián y la forma de convertir radianes en grados y viceversa. Por tanto ya sabemos expresar en radianes ciertos ángulos que suelen aparecernos en grados en muchas ocasiones, como pueden ser ó
. Creo que entonces es el momento de recordar cómo calcular las razones trigonométricas de algunos de estos ángulos del primer cuadrante y también cómo usar esa información para calcular dichas razones trigonométricas para algunos ángulos importantes del resto de cuadrantes.
¿Te ha gustado la entrada? Puedes invitarme a un café, Gauss te lo agradecerá 😉







Supongo yo que, esa «naturalidad», citada en el artículo de la Wikipedia en inglés, viene del hecho de que la longitud del arco de circunferencia es proporcional al ángulo en sí por un lado, y al radio por otro:
Y dado que la expresión de la longitud de la circunferencia es , ¿qué mejor que, en esta última expresión, identificar
, ¿qué mejor que, en esta última expresión, identificar  como el ángulo
como el ángulo  de la expresión de arriba? Y así no tener que introducir un factor de conversión adicional y, a la vista de esto, completamente innecesario.
de la expresión de arriba? Y así no tener que introducir un factor de conversión adicional y, a la vista de esto, completamente innecesario.
Muy bueno. Y el gif extraordinario.
¿Tenéis alguna entrada que explique el concepto Determinante de una matriz y sus usos?
Gracias.
Si hablas inglés, este recurso te parecerá muy útil para entender el concepto y uso de determinante, derivada e integral a fondo. https://www.youtube.com/watch?v=wCZ1VEmVjVo&t=1191s
Saludos!
Información Bitacoras.com
Valora en Bitacoras.com: El pasado mes de mayo de 2014, durante el evento que sirvió como celebración del 50 aniversario de los estudios de Matemáticas en la Universidad de Granada, Juan Medina (uno de los integrantes de la mesa sobre Matemáticas…
Encuentro oportuno citar en este artículo la unidad de medida de los ángulos sólidos: el estereoradián. El mismo concepto del radián llevado a tres dimensiones.
En esta dirección http://es.wikipedia.org/wiki/Estereorradian está descrito con claridad.
El radián tendría más naturalidad matemática si se usara Tau (=2Pi) en lugar de Pi, puesto que, por ejemplo: «1/2Tau rad»=»1/2 circunferencia»=»1/2 vuelta»; es decir, la fracción de los radianes sería la misma que la fracción de circunferencia recorrida por el ángulo. Pero con Pi estamos hablando de las fracciones de la mitad de algo, y esto conlleva a hacer de los radianes un tema abstruso para muchos.
[…] El pasado mes de mayo de 2014, durante el evento que sirvió como celebración del 50 aniversario de los estudios de Matemáticas en la Universidad de Granada, Juan Medina (uno de los integrantes de la mesa sobre Matemáticas y Redes Sociales que tuve el honor de moderar) habló durante su intervención (por cierto, aquí tenéis la presentación que usó) sobre algunas de las cuestiones que le motivaron a crear su plataforma de vídeos. Entre ellas en mi mente quedó concretamente una, que me pareció bastante interesante y que es la que titula este post: ¿qué es un radián? Juan… Lee más »
Y sin embargo, otras expresiones son más sencillas con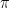 que con
que con  . Por ejemplo, nuestra vieja amiga
. Por ejemplo, nuestra vieja amiga  .
.
Me gusta este tema, ya que el radian es una unidad de medida que se emplea mucho en las Ciencias Físicas al pasar de a r.p.m (revoluciones por minuto), y de ahí saber la velocidad.
a r.p.m (revoluciones por minuto), y de ahí saber la velocidad.
Os dejo un enlace que lo explica mucho mejor:
http://es.wikipedia.org/wiki/Revoluci%C3%B3n_por_minuto
Dedicado a esos físicos que nos enseñaron a pensar como resolver problemas físicos, desde lo más simple hasta lo que cada uno da de sí.
Un cordial saludo
[…] ¿Qué es un radián?: El pasado mes de mayo de 2014, durante el evento que sirvió como celebración … http://t.co/OgjH89jCax #matematicas […]
[…] Bueno, pues ya sabemos lo que es un radián y la forma de convertir radianes en grados y viceversa. Por tanto ya sabemos expresar en radianes ciertos ángulos que suelen aparecernos en grados en muchas ocasiones, como pueden ser ó . Creo que entonces es el momento de recordar cómo calcular las razones trigonométricas de algunos de estos ángulos del primer cuadrante y también cómo usar esa información para calcular dichas razones trigonométricas para algunos ángulos importantes del resto de cuadrantes. […]
Dado Tau=6,28… y Pi=Tau/2, la expesión « » es más sencilla que «
» es más sencilla que « » (véase el «-«). La manera popular de expresar la identidad de Euler («
» (véase el «-«). La manera popular de expresar la identidad de Euler (« «) se debe en realidad a un capricho estético de los matemáticos, que introduce unos pasos de más, convirtiendo al «horrible número negativo» en un número positivo. (Este comentario es una réplica al comentario del señor krollspell)
«) se debe en realidad a un capricho estético de los matemáticos, que introduce unos pasos de más, convirtiendo al «horrible número negativo» en un número positivo. (Este comentario es una réplica al comentario del señor krollspell)
[…] El pasado mes de mayo de 2014, durante el evento que sirvió como celebración del 50 aniversario de los estudios de Matemáticas en la Universidad de Granada, Juan Medina (uno de los integrantes de l… […]
[…] ¿Qué es un radián? […]
Apreciado Derkcopyleft, también soy fan de , pero creo que en este caso no es un capricho la expresión con el uno positivo. Más bien se trata de incluir al cero para que aparezcan los cinco números más importantes relacionados de una forma sencilla; así, además de la base de los logaritmos naturales, pi y la «unidad» de los imaginarios, también tenemos a los neutros de las operaciones fundamentales: El uno para el producto y el cero para la suma.
, pero creo que en este caso no es un capricho la expresión con el uno positivo. Más bien se trata de incluir al cero para que aparezcan los cinco números más importantes relacionados de una forma sencilla; así, además de la base de los logaritmos naturales, pi y la «unidad» de los imaginarios, también tenemos a los neutros de las operaciones fundamentales: El uno para el producto y el cero para la suma.
Saludos.
Más de «Tau versus Pi». Deducción de la Identidad de Euler a partir de la Fórmula de Euler: 1. Con Tau=6,28…=c/(r); «6» y «28» son los primeros números perfectos; véase tauday.com : a) b) c) d) 2. Con Pi=Tau/2=c/(2r); «d» siempre desterrado: a) b) c) d) Este es el curso natural de estas expresiones. Pero Pi (con «P» de «parásito»; Parásito del 2) conduce a encontrarnos con un «-1» que no quieren que veamos. Entonces incluyen un nuevo paso, pero innecesario para relacionar los cinco elementos matemáticos: e) Por lo tanto, el «0» se incluye de manera sencilla sin incluir… Lee más »
Honestamente no creo que eso del Tau pegue, es como una moda hipster: No está mal pero realmente no hay un argumento real para cambiar. Suerte a los seguidores del Tau… yo mientras seguiré usando Pi cuando doy clases, nada más porque me gusta más.
mi duda es si es una unidad de medida, ¿como entender por ejemplo una expresión tipo x + sen x, cuando el sen x no tiene unidad y x si (en radianes)?
En grados sexagesimales la veo absurda, pero en radianes tampoco la veo bien. Podríais ayudarme?
Radianes no es una unidad. Es un número real más al que se le pone un nombre para que que pienses en él como ángulo.
Piensa en la definición de radian: es un arco de circunferencia de longitud igual al radio dividido por la longitud del radio. O sea m/m ó cm/cm ó km/km …
¿ves como el radián no es una unidad de nada sino un simple número real?
Saludos.
Vaya, Albert. Cuidado con los conceptos elementales de secundaria.
El radián no es un arco de circunferencia. Es un ángulo.
Seguro? En el círculo unitario las longitudes de arco son iguales al ángulo en radianes, es este hecho el que ha hecho útiles a los radianes pues son usados para modelar funciones trigonométricas que tienen aplicaciones de situaciones que se repiten una y otra vez. Si te fijas, al modelar funciones trigonométricas como f(x)=asen(bx+c)+d , x no es precisamente un ángulo, puede ser tiempo, posición, etc.
Hola, María. (Aunque no sé si tu nombre es maria o María) La expresión x+senx no la veas como una incongruencia en la x ya sea como grados o radianes. ¡No… sí hay congruencia en la expresión! Simplemente considérala como una función Y= Ax +Bsenx ,así como por ejemplo Y=A+Bt^2, donde si Y es en metros, los coeficientes A y B deben tener en tu caso el valor de 1, pero respectivamente con unidades de metros y metros/seg^2 (para el tiempo t en segundos). Es decir que para tu expresión, A podría ser 1 metro/rad y B podría ser simplemente… Lee más »
[…] la trigonometría se suelen utilizar tres unidades para medir ángulos, la primera de ellas es el radián, la cual es considerada la unidad natural para medir ángulos, esta unidad indica que una […]
Por favor quien me puede ayudar con esta actividad de matemáticas, para el lunes de ante mano gracias transforma las siguientes medidas de grados a radianes :
A. 45°radianes
B. 90° radianes
C. 180 °radianes
D. 270 ° radianes
¡Hola! Alguien me podría explicar de dónde sale o se deduce la fórmula para calcular la medida de un ángulo cualquiera en el sistema radial:
«La medida en radianes de un ángulo en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia».
No fue James Thompson, el fue poeta no matemático