Symmetrieoperationen mit Strecken

Zusammenfassung

Meist sind Industrieregelrecken allein aus technologischen Gründen stabil. Jedoch kann eine interne Rückführung einer Strecke zur Instabilität führen. Auch sind zwei oder mehr in Reihe geschalteten I-Glieder instabil. In diesem Kapitel sind instabile Strecken 1. und 2. Ordnung betrachtet bzw. die instabilen P-T1- und P-T2-Glieder. Die Polstellen instabiler Strecken sind positiv und sind gegenüber Polstellen stabiler Strecken an die Imaginärachse der s-Ebene gespiegelt. Es sind also die Symmetrien zwischen stabilen und instabilen Strecken auch in anderen Bereichen, wie Sprungantworten und Bode-Diagramme, zu erwarten. Somit das Ziel dieses Kapitels ist es, die Symmetrien zwischen stabilen und instabilen Strecken zu finden. Das kommt bei den nachfolgenden Kapiteln zum Nutzen, wenn die Stabilität von Regelkreisen mit instabilen Strecken geprüft wird. Auch die Herleitung von Symmetrieoperationen für Standardregler wird damit erleichtert. Zu allen theoretischen Ergebnissen sind Beispiele oder Übungsaufgaben vorgesehen, die mit MATLAB^®-Skripten begleitet sind.

„Symmetrie schafft eine zugleich wundervolle und lächerliche Verwandtschaft zwischen Objekten, Phänomenen und Theorien.“ Zitat: Herrmann Weyl (2017) Symmetrie. Springer Verlag Berlin Heidelberg

6.1 Stabile und instabile Regelstrecken

Lineare Übertragungsglieder werden meist mittels Differentialgleichungen mit konstanten Koeffizienten, z. B.

$$a_{2} \ddot {x}_{a} (t) + a_{1} \dot{x}_{a} (t) + a_{0} x_{a} (t) = b_{0} x_{e} (t)$$

oder mit einem oder anderen zeitabhängigen Koeffizient

$$a_{2} \ddot {x}_{\text{a}} (t) + a_{1} (t)\dot{x}_{\text{a}} (t) + a_{0} x_{\text{a}} (t) = b_{0} x_{\text{e}} (t)$$

beschrieben. Die Übertragungsglieder mit konstanten Koeffizienten bezeichnet man als LZI-Glieder (lineare zeitinvariante). Dagegen werden die Übertragungsglieder mit zeitabhängigen Koeffizienten LZV-Glieder (lineare zeitvariante) genannt. Die LZV-Glieder wurden in [1] behandelt und kommen in diesem Buch nicht in Betracht.

6.1.1 Polstellen, Sprungantworten

Stabile Strecken haben negative Polstellen. Beispielsweise eine P-T1-Strecke

$$G_{\text{S}} (s) = \frac{K}{{sT_{1} + 1}}$$

(6.1)

hat die Polstelle

$$s_{1} = - \frac{1}{{T_{1} }}$$

(6.2)

mit negativer Realteil und ist somit stabil. Die Sprungantworten von stabilen Strecken erreichen einen bestimmten Beharrungszustand ohne Regelung und werden deswegen auch „Strecken mit Ausgleich“ genannt.

Wird jedoch aus irgendwelchen Gründen die Polstelle Gl. 6.2 an die Imaginärachse der s-Ebene gespiegelt und wird positiv

$$s_{1} = + \frac{1}{{T_{1} }},$$

ändert sich die Übertragungsfunktion Gl. 6.1 zu

$$G_{\text{S}} (s) = \frac{K}{{sT_{1} - 1}}.$$

Solche Strecken haben keinen Ausgleich mehr, erreicht keinen bestimmen Beharrungszustand und werden instabile P-T1-Strecken genannt (siehe z. B. [1]).

Die Sprungantworten von stabilen und instabilen P-T1-Strecken sind die Lösungen von entsprechenden Differentialgleichungen, bei denen auch bestimmte Symmetrie zu merken ist.

$$T_{1} \dot{x}(t) + x(t) = K \cdot y(t) \to x(t) = K \cdot (1 - e^{{ - \frac{t}{{T_{1} }}}} ) \cdot \hat{y}$$

$$T_{1} \, \dot{x}(t) - x(t) = K \cdot \, y(t) \to x(t) = K \cdot (e^{{\frac{t}{{T_{1} }}}} - 1) \cdot \hat{y}$$

Die Sprungantworten von stabilen und instabilen P-T1-Strecken sind in Abb. 6.1 gezeigt.

Abb. 6.1

Sprungantworten eines stabilen (links) und instabilen P-T1-Gliedes

6.1.2 Beispiele von stabilen und instabilen Strecken

Die Instabilität einer Regelstrecke entsteht in der Regel aus zwei Gründen:

• wegen zwei oder mehr in Reihe geschalteten I-Gliedern

• wegen Mitkopplung im Wirkungsplan der Strecke.

Die Mehrheit der Industrieregelrecken ist allein aus technologischen Gründen stabil. Die klassischen Beispiele von instabilen Strecken sind:

• Invertiertes Pendel (Abb. 6.2)

  Abb. 6.2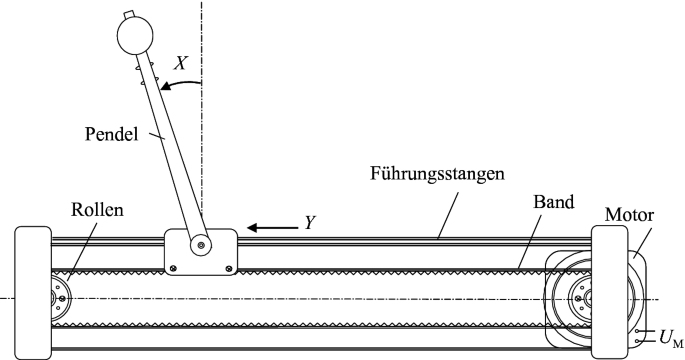

  

  (Quelle [3], Seite 23)

  Invertiertes Pendel.

• Magnetschwebekörper (Abb. 6.3)

  Abb. 6.3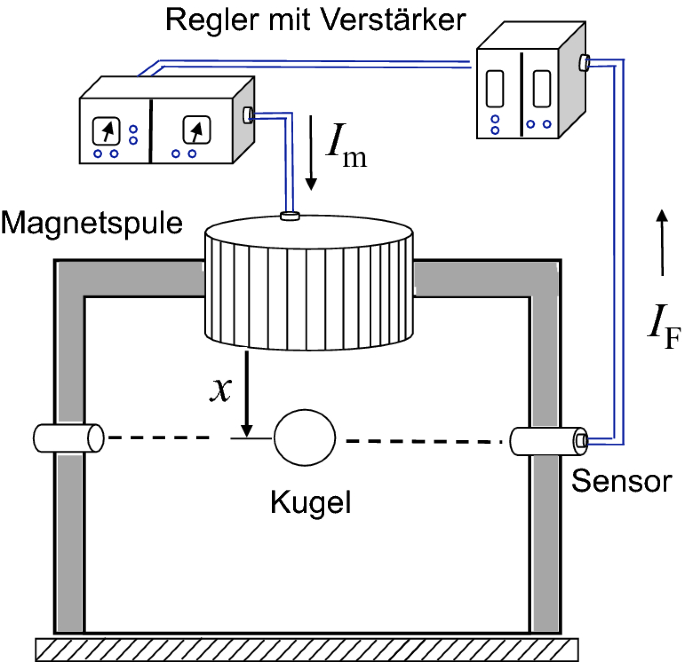

  

  (Quelle [4], Seite 18)

  Magnetschwebekörper.

• Ladebrücke (Abb. 6.4)

  Abb. 6.4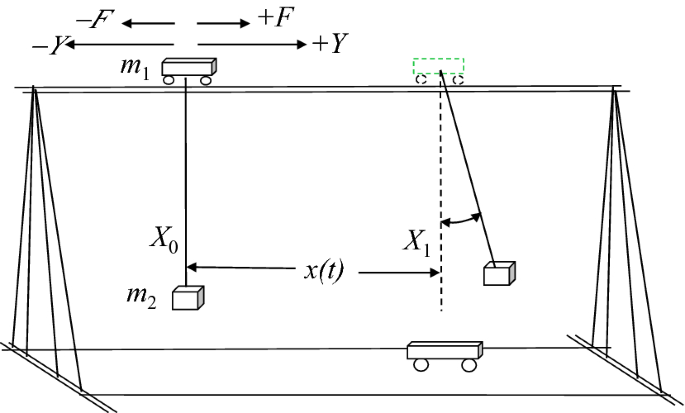

  

  (Quelle [2], Seite 252)

  Ladebrücke.

Invertiertes Pendel

Ein senkrecht stehender Stab befindet sich auf einer Plattform, die fest auf einem Förderband gebunden ist (Abb. 6.2). Durch die horizontalen Bewegungen des Bandes nach links und nach rechts wird der Stab stabilisiert. Regelgröße ist der Winkel X, der mit einem Sensor erfasst wird. Stellgröße Y ist die auf die Plattform wirkende Kraft.

Magnetschwebekörper

Eine Eisenkugel mit der Masse m soll durch die Magnetkraft eines Elektromagneten in einer gewünschten Position X gehalten werden (Abb. 6.3).

Die Position der Kugel wird mithilfe einer Infrarot-Diode und eines Fotoelementes gemessen. Der vom Fotoelement erzeugte Lichtstrom wird mit einem Operationsverstärker in eine Spannung umgeformt.

Der Strom des Permanentmagneten wird von einem Leistungsverstärker erzeugt, der durch das Stellsignal des Reglers angesteuert wird.

Im stationären Schwebezustand befindet sich die Magnetkraft F_m im Gleichgewicht mit der Gewichtskraft P_m:

$$F_{m0} = P_{m} = m \cdot g,$$

wobei g die Erdbeschleunigung ist. Das dynamische Verhalten der Kugel entspricht dem Newton’schen Gesetz und hat im Magnetfeld ein instabiles Verhalten.

Ladebrücke

Stellgröße ist die Kraft F auf die Laufkatze des Kranes bzw. die Beschleunigung Y. Regelgröße ist die Lage X(t) der Last (Abb. 6.4).

Die Ermittlung von Zeitkonstanten der instabilen Regelstrecken ist in [2], Seiten 253, 254, beschrieben.

6.2 Bode-Diagramme von instabilen Strecken

6.2.1 Instabile P-T1-Glieder

Um das Bode-Diagramm eines instabilen P-T₁-Gliedes zu zeichnen, bestimmen wir zunächst aus dem Frequenzgang des Gliedes

$$G(j\omega ) = \frac{K}{{j\omega T_{1} - 1}}$$

seinen Amplitudengang:

$$\left| {G(j\omega )} \right| = \frac{K}{{\sqrt {(\omega T_{1} )^{2} + 1} }}$$

Ein instabiles P-T₁-Glied hat gleicher Amplitudengang, wie ein stabiles P-T₁-Glied.

Der Phasengang ergibt sich bekanntlich als Differenz zwischen Phasen des Zählers und des Nenners:

$$\varphi (\omega ) = \arctan 0 - \arctan \frac{{\omega T_{1} }}{ - 1} = - \arctan \frac{{\omega T_{1} }}{ - 1}$$

$$\varphi (\omega ) = - \pi + \arctan \omega T_{1}$$

Gegenüber einem stabilen P-T₁-Glied mit

$$\varphi (\omega ) = - \arctan \omega T_{1}$$

ist der Phasengang des instabilen P-T1-Gliedes an der (−90°)-Linie gespiegelt und um einen Phasenwinkel von (−π) verschoben, wie in Abb. 6.5 gezeigt ist.

Abb. 6.5

Bode-Diagramme eines stabilen (links) und instabilen P-T1-Gliedes

6.2.2 Instabile P-T2-Glieder

Ein instabiles P-T2-Glied kann aus zwei instabilen P-T1-Gliedern oder aus einer Kombination jeweils eines stabilen und instabilen Gliedes bestehen. In Abb. 6.6 links ist das Bode-Diagramm einer Reihenschaltung von einem stabilen und einem instabilen P-T1-Glied mit unterschiedlichen Zeitkonstanten T₁ und T₂ gezeigt:

Abb. 6.6

Bode-Diagramme von instabilen P-T2-Gliedern

$$G(s) = \frac{K}{{(sT_{1} + 1)(sT_{2} - 1)}}$$

In Abb. 6.6 rechts ist das Bode-Diagramm einer Reihenschaltung von zwei instabilen P-T₁-Gliedern mit gleichen Zeitkonstanten T₁ = T₂ gegeben:

$$G(s) = \frac{K}{{(sT_{1} + 1)(sT_{1} - 1)}} = \frac{K}{{s^{2} T_{1}^{2} - 1}}$$

Wenn T₁ = T₂ ist, dann kompensieren sich die Phasengänge φ₁(ω) und φ₂(ω), sodass die resultierende Kennlinie einem doppelten I-Glied entspricht.

Man erkennt aus Abb. 6.6, dass sich die Asymptote des Amplitudengangs bei der Eckfrequenz, die der rechten Polstelle entspricht, um (−40) dB/Dek ändert, während sich die Asymptote bei der Eckfrequenz der linken Polstellen nur um (−20) dB/Dek ändert.

Auch bei den Phasengängen merkt man die Unterschiede, z. B. im Fall T₁ = T₂ die Phase des instabilen Gliedes ändert sich nicht bei der Eckfrequenz. Eine Phase von (−π) soll jedoch gleich am Anfang zugewiesen werden.

6.2.3 Rezepte für Bode-Diagramme instabiler P-T2-Glieder

Für Bode-Diagramm instabiler P-T2-Glieder gelten folgende Regeln:

Anfangsteil

Der Anfangsteil des Phasengangs liegt bei (−180°), da eine Polstelle mit positivem Realteil in der rechten s-Ebene eine Phasenverschiebung von (−π) mitbringt.

Phasenänderung bei rechten Polstellen

Bei den Eckfrequenzen der rechten Polstellen beträgt die Phasenänderung + 90°, wie beim D-Verhalten.

Amplitudenänderung bei rechten Polstellen

Bei den Eckfrequenzen der rechten Polstellen ändern sich die Asymptoten des Amplitudenganges um (−40) dB/Dek, wie bei einer doppelten linken Polstelle.

6.2.4 Beispiel: instabiles P-T4-Glied

Die Übertragungsfunktion des aufgeschnittenen Kreises ist gegeben:

$$G(s) = \frac{K}{{(sT_{1} + 1)(s^{2} T_{ 2}^{2} - 1)(sT_{3} + 1)}}$$

$$K = 10\quad T_{1} = 0{,}5{\text{ s}}\quad T_{2} = 1{\text{ s}} \quad T_{3} = 5{\text{ s}}$$

Um das Bode-Diagramm zu zeichnen, bestimmen wir die Eckfrequenzen:

$$\omega_{ 1} = \frac{1}{{T_{ 1} }}{\text{ = 2 s}}^{ - 1}$$

$$\omega_{ 2} = \frac{1}{{T_{ 2} }} = 1{\text{ s}}^{ - 1}$$

$$\omega_{\text{3}} = \frac{1}{{T_{3} }} = 0{,}2{\text{ s}}^{ - 1}$$

Anfangsteil

Da kein I-Glied vorhanden ist, verläuft die Asymptote mit der Steigung 0 dB/Dek durch die Ordinate

$$20\lg (K ) = 20\lg (10) = 20{\text{ dB}}.$$

Der Phasengang fängt wegen einer Polstelle mit positivem Realteil nicht bei 0° an, wie es bei stabilen Systemen der Fall wäre, sondern bei (−180°).

Phasenänderung

Die Phase wird bei Eckfrequenzen ω₁ und ω₃ um (−90°) geändert. Bei der Eckfrequenz ω₂, die der Polstelle mit positivem Realteil entspricht, gibt es keine Phasendrehung.

Amplitudenänderung

Die Amplitude wird bei allen Eckfrequenzen um (−20) dB/Dek geändert. Außer der Eckfrequenz ω₂, die der Polstelle mit positivem Realteil entspricht. Bei positiver Polstelle gibt es Steigungsänderung (−40) dB/Dek.

Das Bode-Diagramm ist in Abb. 6.7 gezeigt. Auch das mit dem MATLAB® ermittelte Bode-Diagramm ist in Abb. 6.7 eingetragen.

Abb. 6.7

Bode Diagramm eines instabilen P-T4-Gliedes

s=tf(‘s’); K=10;T1=0.5; T2=1; T3=5; G0=K/((1+s*T1)*(s*T2-1)*(s*T2+1)*(s*T3+1)); bode(G0); grid

6.3 Übungsaufgaben mit Lösungen

6.3.1 Aufgaben

Aufgabe 6.1

In Abb. 6.8 sind zwei Bode-Diagramme von jeweils zwei P-T3-Gliedern gezeigt. Welches Glied ist instabil?

Abb. 6.8

Bode-Diagramme von P-T3-Gliedern zu Aufgabe 6.1

Aufgabe 6.2

In Abb. 6.9 sind drei Bode-Diagramme von jeweils drei P-T2-Gliedern gezeigt. Welche Glieder sind instabil?

Abb. 6.9

Bode-Diagramme von P-T2-Gliedern zu Aufgabe 6.2

6.3.2 Lösungen

Lösung zu Aufgabe 6.1

Das Glied G₂(s) ist instabil, da der Phasengang bei φ = −180° beginnt.

Zur Lösungskontrolle:

$$G_{1} (s) = \frac{3{,}2}{(0{,}5s + 1)(s + 1)(1{,}5s + 1)}$$

$$G_{2} (s) = \frac{3{,}2}{(0{,}5s + 1)(s + 1)(1{,}5s - 1)}$$

Lösung zu Aufgabe 6.2

Die Eckfrequenz bei allen drei Bode-Plots ist ω = 1 s⁻¹, d. h. bei allen Gliedern gilt T₁ = T₂.

Das Glied G₁(s) ist stabil, da der Phasengang bei φ = 0° beginnt und sich bis φ = −180° ändert. Die Amplitudenänderung beträgt (−40)  dB/Dek bei der Eckfrequenz, was auch auf einen stabilen P-T2-Glied mit T₁ = T₂ deutet.

Das Glied G₂(s) ist instabil. Es besteht aus einem stabilen und einem instabilen P-T1-Glied, dessen Phasengänge sich gegenseitig kompensieren, sodass der resultierende Phasengang eine Gerade bei φ = −180° ist.

Das Glied G₃(s) ist instabil und besteht aus zwei instabilen P-T1-Gliedern. Sein Phasengang wiederholt sich den Phasengang des stabilen P-T2-Gliedes, ist jedoch an der (−180°)-Linie gespiegelt und um einen Phasenwinkel (−n · π) verschoben (hier ist n = 2).

Zur Lösungskontrolle:

$$G_{1} (s) = \frac{0{,}5}{{(s + 1)^{2} }}$$

$$G_{2} (s) = \frac{0{,}5}{{(s^{2} - 1)}}$$

$$G_{3} (s) = \frac{0{,}5}{{(s - 1)^{2} }}$$