Propositional logic is a branch of mathematics that studies the logical relationships between propositions (or statements, sentences, assertions) taken as a whole, and connected via logical connectives.
In this article, we have covered in detail about propositional logic and related topics.
What is Logic?
Logic is the basis of all mathematical reasoning and all automated reasoning. The rules of logic specify the meaning of mathematical statements. These rules help us understand and reason with statements such as –
[Tex]\exists~x~such~that~x~\neq~a^2~+~b^2,~where~\:x,~a,~b\in~Z[/Tex]
Which in Simple English means “There exists an integer that is not the sum of two squares“.
Importance of Mathematical Logic
The rules of logic give precise meaning to mathematical statements. These rules are used to distinguish between valid and invalid mathematical arguments. Apart from its importance in understanding mathematical reasoning, logic has numerous applications in Computer Science, varying from the design of digital circuits to the construction of computer programs and verification of the correctness of programs.
Propositional Logic
What is a Proposition? A proposition is the basic building block of logic. It is defined as a declarative sentence that is either True or False, but not both. The Truth Value of a proposition is True(denoted as T) if it is a true statement, and False(denoted as F) if it is a false statement. For Example,
- The sun rises in the East and sets in the West.
- 1 + 1 = 2
- ‘b’ is a vowel.
All of the above sentences are propositions, where the first two are Valid(True) and the third one is Invalid(False). Some sentences that do not have a truth value or may have more than one truth value are not propositions. For Example,
- What time is it?
- Go out and Play
- x + 1 = 2
The above sentences are not propositions as the first two do not have a truth value, and the third one may be true or false. To represent propositions, propositional variables are used. By Convention, these variables are represented by small alphabets such as [Tex]p,\:q,\:r,\:s [/Tex]. The area of logic which deals with propositions is called propositional calculus or propositional logic. It also includes producing new propositions using existing ones. Propositions constructed using one or more propositions are called compound propositions. The propositions are combined together using Logical Connectives or Logical Operators.
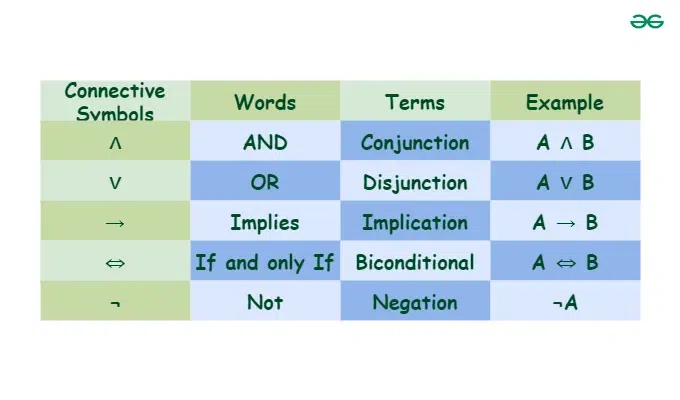
Propositional Logic
Truth Table
Since we need to know the truth value of a proposition in all possible scenarios, we consider all the possible combinations of the propositions which are joined together by Logical Connectives to form the given compound proposition. This compilation of all possible scenarios in a tabular format is called a truth table. Most Common Logical Connectives-
1. Negation
If [Tex]p [/Tex]is a proposition, then the negation of [Tex]p [/Tex]is denoted by [Tex]\neg p [/Tex], which when translated to simple English means- “It is not the case that p” or simply “not p“. The truth value of -p is the opposite of the truth value of p. The truth table of -p is:
Example, Negation of “It is raining today”, is “It is not the case that is raining today” or simply “It is not raining today”.
2. Conjunction
For any two propositions [Tex]p [/Tex]and [Tex]q [/Tex], their conjunction is denoted by [Tex]p\wedge q [/Tex], which means “[Tex]p [/Tex]and [Tex]q [/Tex]“. The conjunction [Tex]p\wedge q [/Tex]is True when both [Tex]p [/Tex]and [Tex]q [/Tex]are True, otherwise False. The truth table of [Tex]p\wedge q [/Tex]is:
Example, Conjunction of the propositions [Tex]p [/Tex]– “Today is Friday” and [Tex]q [/Tex]– “It is raining today”, [Tex]p\wedge q [/Tex]is “Today is Friday and it is raining today”. This proposition is true only on rainy Fridays and is false on any other rainy day or on Fridays when it does not rain.
3. Disjunction
For any two propositions [Tex]p [/Tex]and [Tex]q [/Tex], their disjunction is denoted by [Tex]p\vee q [/Tex], which means “[Tex]p [/Tex]or [Tex]q [/Tex]“. The disjunction [Tex]p\vee q [/Tex]is True when either [Tex]p [/Tex]or [Tex]q [/Tex]is True, otherwise False. The truth table of [Tex]p\vee q [/Tex]is:
Example, Disjunction of the propositions [Tex]p [/Tex]– “Today is Friday” and [Tex]q [/Tex]– “It is raining today”, [Tex]p\vee q [/Tex]is “Today is Friday or it is raining today”. This proposition is true on any day that is a Friday or a rainy day(including rainy Fridays) and is false on any day other than Friday when it also does not rain.
4. Exclusive Or
For any two propositions [Tex]p [/Tex]and [Tex]q [/Tex], their exclusive or is denoted by [Tex]p\oplus q [/Tex], which means “either [Tex]p [/Tex]or [Tex]q [/Tex]but not both”. The exclusive or [Tex]p\oplus q [/Tex]is True when either [Tex]p [/Tex]or [Tex]q [/Tex]is True, and False when both are true or both are false. The truth table of [Tex]p\oplus q [/Tex]is:
Example, Exclusive or of the propositions [Tex]p [/Tex]– “Today is Friday” and [Tex]q [/Tex]– “It is raining today”, [Tex]p\oplus q [/Tex]is “Either today is Friday or it is raining today, but not both”. This proposition is true on any day that is a Friday or a rainy day(not including rainy Fridays) and is false on any day other than Friday when it does not rain or rainy Fridays.
5. Implication
For any two propositions [Tex]p [/Tex]and [Tex]q [/Tex], the statement “if [Tex]p [/Tex]then [Tex]q [/Tex]” is called an implication and it is denoted by [Tex]p\rightarrow q [/Tex]. In the implication [Tex]p\rightarrow q [/Tex], [Tex]p [/Tex]is called the hypothesis or antecedent or premise and [Tex]q [/Tex]is called the conclusion or consequence. The implication is [Tex]p\rightarrow q [/Tex]is also called a conditional statement. The implication is false when [Tex]p [/Tex]is true and [Tex]q [/Tex]is false otherwise it is true. The truth table of [Tex]p\rightarrow q [/Tex]is:
One might wonder that why is [Tex]p\rightarrow q [/Tex]true when [Tex]p [/Tex]is false. This is because the implication guarantees that when [Tex]p [/Tex]and [Tex]q [/Tex]are true then the implication is true. But the implication does not guarantee anything when the premise [Tex]p [/Tex]is false. There is no way of knowing whether or not the implication is false since [Tex]p [/Tex]did not happen. This situation is similar to the “Innocent until proven Guilty” stance, which means that the implication [Tex]p\rightarrow q [/Tex]is considered true until proven false. Since we cannot call the implication [Tex]p\rightarrow q [/Tex]false when [Tex]p [/Tex]is false, our only alternative is to call it true.
This follows from the Explosion Principle which says: “A False statement implies anything” Conditional statements play a very important role in mathematical reasoning, thus a variety of terminology is used to express [Tex]p\rightarrow q [/Tex], some of which are listed below.
“If p, then “q”p is sufficient for q””q when p””a necessary condition for p is q””p only if q””q unless ≠p””q follows from p”
Example, “If it is Friday then it is raining today” is a proposition which is of the form [Tex]p\rightarrow q [/Tex]. The above proposition is true if it is not Friday(premise is false) or if it is Friday and it is raining, and it is false when it is Friday but it is not raining.
6. Biconditional or Double Implication
For any two propositions [Tex]p [/Tex]and [Tex]q [/Tex], the statement “[Tex]p [/Tex]if and only if(iff) [Tex]q [/Tex]” is called a biconditional and it is denoted by [Tex]p\leftrightarrow q [/Tex]. The statement [Tex]p\leftrightarrow q [/Tex]is also called a bi-implication. [Tex]p\leftrightarrow q [/Tex]has the same truth value as [Tex](p\rightarrow q) \wedge (q\rightarrow p) [/Tex]The implication is true when [Tex]p [/Tex]and [Tex]q [/Tex]have same truth values, and is false otherwise. The truth table of [Tex]p\leftrightarrow q [/Tex]is:
Some other common ways of expressing [Tex]p\leftrightarrow q [/Tex]are:
“p is necessary and sufficient for q””if p then q, and conversely””p if q”
Example, “It is raining today if and only if it is Friday today.” is a proposition which is of the form [Tex]p\leftrightarrow q [/Tex]. The above proposition is true if it is not Friday and it is not raining or if it is Friday and it is raining, and it is false when it is not Friday or it is not raining. Exercise:
1) Consider the following statements:
- P: Good mobile phones are not cheap.
- Q: Cheap mobile phones are not good.
- L: P implies Q
- M: Q implies P
- N: P is equivalent to Q
Which one of the following about L, M, and N is CORRECT?(Gate 2014)
(A) Only L is TRUE.
(B) Only M is TRUE.
(C) Only N is TRUE.
(D) L, M and N are TRUE.
For solution, see GATE | GATE-CS-2014-(Set-3) | Question 11
2) Which one of the following is not equivalent to p?q (Gate 2015)
[Tex](A)(\neg p \vee q)\wedge(p \vee \neg q ) (B)(\neg p \vee q)\wedge(q \rightarrow p ) (C)(\neg p \wedge q)\vee(p \wedge \neg q ) (D)(\neg p \wedge \neg q)\vee(p \wedge q ) [/Tex]
For solution, see GATE | GATE-CS-2015 (Set 1) | Question 65
Please Login to comment...