Introductory Remarks About the Mémoire (1761/1768)

Abstract

The historical importance of Lambert’s Mémoire turns out evident as soon as one realizes the issues tackled by the Swiss. There is little doubt that fame goes to the first part of the article, in which Lambert, showing a high level of skill with such then-recent analytic tools like continued fractions, demonstrates with unusual rigour for the 18th century standards the irrationality of $\pi$. The issue of the nature of this constant had taken a new impulse since the herculean efforts by Ludolph van Ceulen at the end of the 16th century with the use of new analytic tools and their application to some geometric problems. Authors like Gregory, Huygens, Mengoli, Leibniz or Wallis faced these issues, and in particular, the circle-squaring problem, in which $\pi$ played a central role. Lambert takes up the baton of this analytic tradition —enriched by Euler with his first systematic study of continued fractions— and settles the question of its irrationality.

Therefore the circumference of the circle is not to the diameter as an integer number to an integer number.

—J. H. Lambert Mémoire.

1 Introduction and Context

The historical importance of Lambert’s Mémoire turns out evident as soon as one realizes the issues tackled by the Swiss.¹ There is little doubt that fame goes to the first part of the article, in which Lambert, showing a high level of skill with such then-recent analytic tools like continued fractions, demonstrates with unusual rigour for the 18th century standards the irrationality of $\pi$. The issue of the nature of this constant had taken a new impulse since the herculean efforts by Ludolph van Ceulen at the end of the 16th century with the use of new analytic tools and their application to some geometric problems. Authors like Gregory, Huygens, Mengoli, Leibnizor Wallis faced these issues, and in particular, the circle-squaring problem, in which $\pi$ played a central role. Lambert takes up the baton of this analytic tradition —enriched by Euler with his first systematic study of continued fractions— and settles the question of its irrationality.

In any case, it may be necessary to clarify this last statement, since doubts have arisen around Lambert’s proof. Such is the case of Ferdinand Rudio or Felix Klein (following the former), who refered to Lambert’s proof as incomplete in contrast to authors like Alfred Pringsheim or J. W. L. Glaisher.² Pringsheim wrote that Lambert’s work is «highly ingenious and flawlessly in essence»,³ whereas Glaisher in his article On Lambert’s Proof of the Irrationality of $\pi$, and on the Irrationality of certain other Quantities, compared his proof with that by Legendre —a proof that filled in the gaps of Lambert’s according to some interpretations— in the following terms:⁴

Although Legendre’s method is quite as rigorous as that on which it is founded, still, on the whole, the demonstration of Lambert seems to afford a more striking and convincing proof of the truth of the proposition.

And he added up, after his presentation, that:

That Lambert’s proof is perfectly rigorous and places the fact of the irrationality of $\pi$ beyond all doubts, is evident to every one who examines it carefully; and considering the small attention that had been paid to continued fractions previously to the time at which it was written, it cannot but be regarded as a very admirable work.

As will be seen later, the interpretation given in our analysis of Lambert’s proof will show basically one single conflicting point in his demonstration; one step taken by Lambert that is not obvious and needs proof, but that would not deserve to be the source of criticism considering the epoch in which it was elaborated (1761/1768).

Although it is difficult to advance this claim with absolute certainty, it could have ocurred with Lambert and his proof what allegedly happened to Euler in connection with his proof of the irrationality of e. Some historians consider Euler’s «proof» to be the statement included in the last chapter of the first volume of his Introductio. There,⁵ Euler presented an infinite regular continued fraction for $\frac{e-1}{2}$, which ensures its irrationality, but did not provide any justification, limiting himself to comment: «This result can be confirmed by infinitesimal calculus». But what really happened is that Euler had already published a rigorous proof in a much less known work.⁶

Lambert could be in the same situation: on the one hand he published an article whose title clearly indicates the topic to be covered, and the content of which is aimed at a more general audience —this is part V of his (Lambert 1766/1770), entitled⁷ Preliminary knowledge for those who seek to square and rectify the circle—, therefore an accessible work in which he made some claims about the nature of $\pi$; and on the other hand we have a more academic work without a direct reference in its title to the circle-squaring problem or $\pi$, and directed to a smaller audience —his (Lambert 1761/1768)— and therefore a much less known work that, on the contrary, does include a rigorous proof of the irrationality of $\pi$.

An example of this interpretation could be the case of A. L. Crelle, who in his translation of Legendre’s work (German 3rd edition, 1837) noted, in reference to (Lambert 1766/1770), that Lambert’s proof of the irrationality of $\pi$ is less rigorous than Legendre’s.⁸ In more recent literature, we have an example in [Beckmann 1971, pp. 170, 171], where it is said —also making reference to (Lambert 1766/1770)— that:

Lambert investigated certain continued fractions and proved the following theorem:

If x is a rational number other than zero, then $\tan x$ cannot be rational.

adding that «Legendre, in his Elementes de Géometrie (1794) proved the irrationality of $\pi$ more rigorously [...]».⁹ Exactly in the same vein is [Ebbinghaus et al. 1988, p. 149], where the authors, making reference to (Lambert 1766/1770), mention that «Lambert’s proof is not completely rigorous because it lacks a lemma on the irrationality of certain continued fractions», lemma that would later be proven by Legendre.

Perhaps, we should say that Lambert is partly to blame for propagating this view, since in [Lambert 1766/1770, p. 167] he expressed himself in the following terms:

Since, therefore, the tangent of every rational arc is irrational, then, conversely, the arc of every rational tangent is irrational. For, if one were to assume the arc to be rational, then, contrary to the assumption, the tangent would be irrational by virtue of what was initially proven.¹⁰

In any case, this interpretation may partially account for this type of statements, although it should not be taken as a definitive explanation. For instance, we have already mentioned the case of Rudio, who in (Rudio 1892) seems to make explicit reference to Lambert’s Mémoire when he talks about the fact that there is a gap in his proof, and that this gap would be eventually filled in by Legendre in his aforementioned note. Unfortunately, he does not indicate the specific place in Lambert’s reasoning where he considers the problem to be at. In any case, Pringsheim in his Ueber die ersten Beweise der Irrationalität von e und $\pi$, comments, referring among others to Rudio and Klein, that from his point of view the interpretation according to which Legendre completed Lambert’s proof is not well founded, and that Lambert proved this (and other facts¹¹) «with a rigor that is truly exceptional for his time», bringing out the fact that Lambert included a proof of convergence whilst Legendre did not.

The general impression is that mathematicians in this period were heavily oriented towards problems and methods of calculation, general formulas and numerical approximation, while the orientation taken by Lambert in 1761/1768 was of a clearly more theoretical and/or logical tendency.¹² We are dealing in some sense with a pioneering result, a little too early for this time, falling more squarely within the general orientation of mathematics from approximately 1825 onwards. In this respect, it is insightful what A. von Braunmühl writes in [Cantor 1908, pp. 447–448] after naming some authors and their connection with $\pi$:

Lambert’s contemporaries however seem either to have missed his work, or to have ignored the significance of the step that he made by establishing the knowledge of the nature of number $\pi$ by means of this exact proof [...] The whole nature of Lambert’s proof procedure, with its goal of absolute exactness, remained thus quite outside of the sphere of activity of their contemporaries, directed almost exclusively to the formal expansion of mathematics, and so it becomes understandable that it could be ignored.¹³

Leaving aside the irrationality of $\pi$, it is specially interesting that Lambert in this paper makes one of the first modern uses of hyperbolic functions, although the terminology he uses is not that which we currently use (he speaks of «logarithmic transcendent quantities»). After noting the similarity between the series representation of the circular and hyperbolic trigonometric functions, he looks into the reason behind that similarity, a reason that he finds in the fact that while the former parameterizes the circumference, the latter parameterizes the hyperbola.

Lastly and near the end of the work, Lambert makes the first modern distinction between algebraic and transcendental irrationals. Throughout the paper, it is possible to grasp how the modern meaning of the term «transcendent» emerges, going from representing non-finitely expressible irrational quantities, that is to say, irrational quantities that cannot be finitely expressed by means of usual algebraic operations (addition, subtraction, multiplication, division and extraction of roots), to quantities that are not roots of algebraic equations. In any case, this use did not become standard until new results in the field of algebra and number theory —Abel-Ruffini’s theorem and Liouville’s theorem— motivated the change from the old theoretical framework («to be expressible») to the new one («to be root»). The final part of the work culminates concretely and notably with the conjecture of the transcendence of $\pi$ and the impossibility of squaring the circle.

In general, the Mémoire is not a self-contained work, in the sense that it does not allow a gentle and easy reading. It is enough to make this clear by bringing up what Legendre says in Note VI of his Elements of Geometry —entitled Where it is shown that the ratio of the circumference to the diameter and its square are irrational numbers, and in which he gives a new, much shorter and simpler proof of this fact— about (only) the part dedicated to the proof of the irrationality of $\pi$:

We already know one proof of this proposition that has been given by Lambert in the Memoirs of Berlin, year 1761; but, as this proof is long and difficult to follow, we have tried to shorten and simplify it.¹⁴

That is why a guide is useful and even necessary for those who want to read and understand this important work without falling into the temptation to abandon and go directly to simpler demonstrations of irrationality, such as the one by Legendre, or the more modern by Ivan Niven; needless to say for those who wants to delve into the reading of the entire article. A summary of what one could find —and indeed what the author of these lines found— in the search for such a guide would be the following.

To begin with, this is the first definitive English translation to be published.¹⁵ The works that are constantly referred to are commentaries or translations of certain parts of the Mémoire. What there is is an annotation in French of the complete work in its original language; it is (Speiser 1946–1948). This work by Andreas Speiser, who edited Lambert’s mathematical work, is the classic work to which historians often referred —for example [Serfati 1992, p. 75]— but the ten footnotes that accompany the edition of the Mémoire are far from solving all the obstacles one would face when reading it. It has been decided to also include Speiser’s annotations (see Appendix C) due to the classic nature of his work, so that in any case the reader will be able to judge for himself.¹⁶ What is undeniable is the meticulousness of his analysis, as Speiser corrects every single of Lambert’s errors or misprints, even when some of them are not easy to locate. Sometimes he includes the correction in a footnote, other times he introduces it directly in the main body of the text, including the original in a footnote, and some other times he corrects the text without mentioning it.

Further comments on this work,¹⁷ especially regarding the demonstration of the irrationality of $\pi$, can be found in [Struik 1969, pp. 369–374] and [Berggren 1997, pp. 369–374], although both of them contain the same material: only points 37–51 of the Mémoire (with no extensive analysis). The first 37 points and points from 51 to 91 are missing and they are not of little interest as we have already mentioned briefly.

One of the most relevant works that addresses Lambert’s Mémoire is [Serfati 1992, pp. 62–83], which, however, does not focus on technical details but offers a more global approach to the work, in particular about the points where Lambert touches on issues of irrationality and transcendence; in his more recent work ([Serfati 2018, pp. 179–184]), one finds basically the same material. On the other hand, for more technical details readers are referred to the important contribution by (Baltus 2003), who addresses therein the main problematic part of Lambert’s proof.

On the other hand, Martin Mattmüller and Franz Lemmermeyer in their edition of the correspondence between Euler and Goldbach, mention an article by Bruce J. Petrie (Petrie 2009) «for a modern exposition of Lambert’s proof».¹⁸ Certainly this is a helpful work containing detailed explanations —based in part (Struik 1969)—, but for most of Lambert’s proof (points 1–37) Petrie simply refers to [Chrystal 1906, pp. 517–523], who does not follow it literally but makes a modern and very technical approach, and to the work by [Brezinski 1991, 109–111], who only makes a few comments on the three pages he devotes to Lambert’s proof. In fact, Brezinski refers to (Struik 1969) for an English translation.

A bit out of the «most typical», and regarding Lambert’s treatment of the hyperbolic functions contained in the Mémoire (Lambert is a pioneer in this), there is a valuable work —(Barnett 2004)— which analyzes the role played by Lambert in this issue, although there are things that the author leaves behind and that Lambert does include and use (such as the curious concept of «prime tangent»). Also in (Juhel 2009) one can find a useful analysis of both this issue and the parts of the Mémoire devoted to the irrationality of $\pi$ and the conjecture launched by Lambert about the transcendence of $\pi$.

Although this brief summary does not cover all the material on the subject, what has been said should help to get an idea of the gaps surrounding this important work and justify the suitability of the publication of an annotated translation of Mémoire sur quelques propriétés remarquables des quantités transcendentes circulares et logarithmiques (1761/1768).

By the way, this double dating may require an explanation. The years 1761/1768 probably refer to the delivery period of the different works included in this issue of the Memoirs of the Berlin Academy. In the particular case of Lambert’s Mémoire, we know that it was written a few months after his (Lambert 1766/1770), something he did in 1766.¹⁹ Karl Bopp indicates that Lambert wrote the Mémoire in 1767, and that it was published in 1768, as the Academy’s own volume indicates. In fact, Lambert made an annotation in his Monatsbuch, dated July 1767, which begins as follows:

Sur une proprieté remarquable des quantités transcendentes

circulaires et Logarithmiques. Diss[ertatio] acad[emica].

In addition, the minutes reported on the Academy had established the holding of weekly plenary sessions every Thursday. They were attended by ordinary members and works pending publication were read out. In the plenary session of Thursday, September 17, 1767, the reading of Lambert’s Mémoire is registered.²⁰

2 Outline

What follows is a brief outline of the Mémoire. It is just intended to provide a general idea of Lambert’s paper.

• §.  1.–§.  3. (pp. 265–267)

  • $*$ Brief historical introduction on $\pi$.

  • $*$ Intuitive explanation of the reasons to expect the irrationality of $\pi$.

  • $*$ What is intended to demonstrate:

    

    (4.1)

    and how to do it: by using Euclid’s Algorithm for the calculation of the greatest common divisor.

• §.  4.–§.  15. (pp. 267–275)

  • $*$ Continued fraction expression for the tangent.

  • $*$ Proof by induction of said expression.

  • $*$ Particular cases in which (4.1) can be proved.

• §.  16.–§.  30. (pp. 276–286)

  • $*$ Search and proof by induction for the general term by recurrence of thesuccession of the convergents $\{\frac{p_{n}}{q_{n}}\}$ of the continued fraction of $\tan v$.

  • $*$ Search and proof by induction —on the basis on this general term byrecurrence— of the general term of this very sequence dependent only on n.

  • $*$ Proof that this sequence actually converges to $\tan v$.

• §.  31.–§.  51. (pp. 286–297)

  • $*$ Series expression for the tangent from the convergents.

  • $*$ Proof by Reductio Ad Absurdum of (4.1).

  • $*$ As an immediate consequence, 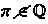since $\tan \frac{\pi }{4}=0\;\in \;\mathbb {Q}$.

• §.  52.–§.  71. (pp. 297–304)

  • $*$ Results that motivate the introduction of the concept of «prime tangent».

  • $*$ The case of $\tan 45^{\circ }$.

  • $*$ Results on prime tangents.

  • $*$ The similarity with the cosine (completely analogous to the tangent, we wouldhave the concept of prime cosine with similar results) and the differencewith the sine (not in this case).

• §.  72.–§.  88. (pp. 304–320)

  • $*$ Search for fractions that approximate the continued fraction both by defaultand by excess. Continued fraction expression of the cotangent.

  • $*$ Similarity between the infinite series of the «circular transcendentquantities» (sine and cosine) and the «logarithmic transcendentquantities» (hyperbolic sine and cosine). Continued fraction expression ofsome rational expressions of $e^x$. New irrationality result:

    

  • $*$ Link between the «logarithmic transcendent quantities» and the hyperbolaequilateral, in the same way that this link occurs between the «circulartranscendent quantities» and the circumference.

  • $*$ New irrationality results: hyperbolic tangent and natural logarithms.

  • $*$ What appears to be an affirmation of the transcendence —no longer in theclassical sense of the term, but in its modern sense— of the number e.Irrationality results for hyperbolic logarithms.

  • $*$ How the concept of «prime tangent» applies equally to the hyperbolic case.

  • $*$ One last look at the analogy between «circular transcendent quantities» and«logarithmic transcendent quantities».

• §.  89.–§.  91. (pp. 320–322)

  • $*$ First modern differentiation between irrational in terms of algebraic andtranscendental.

  • $*$ Conjecture of the transcendence of the «logarithmic transcendentquantities» and the «circular transcendent quantities».

  • $*$ Conjecture of the significance of $\pi$ and therefore of the impossibility ofsquaring the circle.