Introduction

Structural engineers are usually interested in using simplified methods in modeling and design of structures. Over recent decades, one of the research interests in the area of infilled frame has been to replace the infill panel with an equivalent diagonal strut in framed structures. Using the “compression strut” concept, the effect of infills on the global and local behavior of buildings subjected to seismic loads can be achieved through nonlinear analysis. Nowadays, this simplified technique has widespread application in seismic design verification, vulnerability or damage assessment of existing infilled frames, strengthening, and/or risk analysis (d’Aragona et al., 2018; Di Sarno & Wu, 2020; Furtado et al., 2015; Pradhan et al., 2021; Risi et al., 2018).

The approach was initially introduced by Polyakov (1960) and later developed by Holmes (1961) and Smith (1962). Further studies by Smith and Carter (1969), Mainstone and Weeks (1970), and Mainstone (1972) led to the use of the diagonal strut model in design codes, for assessment and strengthening purposes. Nowadays, this method is considered by a number of design codes and standards, e.g., ASCE/SEI 41-17 (2017), NZSEE 2017 (New Zealand Seismic Code) (2017), Eurocode 8 (2004), and FEMA 306 (2000), as a simple and effective technique to calculate the in-plane stiffness and lateral strength of infilled frames. Over the past 3 decades, researchers have proposed more complex macro-models, known as multi-strut models, to study local effects of the infill wall on the surrounding frame. This approach was followed in addition to the general behavior of the system along with the position of plastic hinges formed in a column or a beam as well as the distribution of internal forces in frame members (Chrysostomou, 1991; Chrysostomou et al., 2002; El-Dakhakhni et al., 2003; Pashaie & Mohammadi, 2019; Yekrangnia & Mohammadi, 2017).

In different countries, the infill walls are built with a variety of materials and with different construction techniques. Although masonry is the oldest and most widespread material used as infills, the application of a sandwich panel in framed structures has grown in recent years, particularly in regions with high seismic activities (Hashemi et al., 2018a). The concrete sandwich panel (CSP), also known as 3D-panel, has been one of the infills that needs further study due to its recency in the field of “infilled frame” and its considerable influence on the in-plane behavior of combined panel-frame systems. A concrete sandwich panel comprises a polystyrene sheet placed between two layers of a galvanized steel wire mesh. These two layers of the steel wire mesh are connected together using shear connectors, which lead to the out-of-plane stability of the panel (Fig. 1). Once the panel is placed in the right position, a shotcrete layer is applied on both sides of the panel. Using this prefabricated system, structural and architectural advantages such as excellent thermal and acoustic efficiency, and good out-of-plane performance can be expected. In addition to the stiffening and strengthening effects of the CSPs on the frame structures, saving materials and labor costs and reducing construction time can be obtained toward improved on-site productivity. These advantages have led to the use of CSP infills, over recent years, especially in mid- and high-rise buildings with a high level of seismic importance factor (Hashemi et al., 2018a, 2018b; Teeuwen et al., 2010).

Fig. 1
figure 1

3D view of concrete sandwich panel

Full size image

There are a limited number of studies working on the seismic behavior of Concrete Sandwich Panel-Infilled Steel Frames (CSP-ISF). The available studies on the concrete sandwich panels have mainly focused on load-bearing wall structures (Hou et al., 2019; Palermo et al., 2013; Pavese & Bournas, 2011; Rezaifar et al., 2008; Ricci et al., 2013a). Kabir et al. (2006) used a quasi-static cyclic testing approach to explore the seismic response of CSPs bounded by steel frames. They found that CSPs can be used as a strengthening method for existing steel frame buildings and the feasibility resistance of such combined systems was confirmed. Design rules for hybrid infilled frames, i.e., steel frames separated from precast concrete infill panels, having different geometries for window opening were developed by Teeuwen et al. (2010) through experimental and numerical investigations. Hoenderkamp et al. (2010) reported the results of experimental and finite-element studies on the lateral stiffness and strength of steel frames infilled with precast concrete panels having a discrete panel-to-frame interface connection. The specimens included two full-scale, one-story, and one-bay infilled frames. A significant increase in the lateral stiffness of infilled frames, nearly 12 and 10 times more than that of the corresponding bare frame, was achieved. Hou et al. (2012) conducted a number of cyclic tests on the full-scale one-story and one-bay specimens to study the hysteretic behavior of CSP-ISFs. The effect of six parameters including the panel-frame connection method, beam-to-column connection type, panel’s type, position and thickness, and column’s orientation were considered. The composite panels used as infills exhibited a better integration in comparison to the traditional panels. Several damage modes including concrete spalling around the embedded parts, local buckling of beam flange, and beam’s weld fracture were observed as the main failure modes of CSP-ISF specimens.

In 2018, a research program was conducted by Hashemi et al. (2018a, 2018b), both experimentally and numerically, to investigate the influence of two main factors on the in-plane lateral behavior of CSP-ISFs. These factors were the aspect ratio and frame-to-panel interface conditions. Based on the results presented in these studies, the addition of CSP led to a significant increase in the initial stiffness and lateral strength, equivalent viscous damping ratio, as well as energy dissipation capacity of the steel frames. Moreover, with separating the CSP infill from the surrounding frame, it was found that the isolated infilled frame behaves differently compared to the infilled frame with a full (panel-to-frame) connection. Abbas et al. (2019) carried out an experimental test on CSP subjected to blast load. The precast reinforced concrete wall panels showed greater capability of absorbing and dissipating energy compared to other common building systems.

As mentioned earlier, the seismic behavior of CSP-ISF is a common concern, due to the novelty of the subject. The study presented here attempts to provide suggestions for macro-modeling of CSP-ISFs for nonlinear analysis of these structures. The main objective of the present study is to model concrete sandwich infill panels using a simplified micro-modeling approach by taking CSP infill as a diagonal compressive strut form. First, the most common strut models available in the literature were reviewed. A brief description of the experimental work exploring the in-plane lateral behavior of CSP-ISFs, carried out by the authors, was subsequently presented. Next, a 2D finite-element (FE) micro-model was developed through DIANA software. Then, using the validated material properties in FE models against experimental data, a comparison was made for several macro-modeling approaches of CSP-ISF. Finally, modified formulas including reduction factors of the lateral stiffness and ultimate strength were proposed as a practical method to estimate the in-plane behavior of CSP-ISFs with a central opening.

Background of strut models for infill walls

In the early 1960s, it was found that the infill can be replaced by a pin-jointed diagonal compressive strut with the same thickness and same material as the infill wall. Over the past few decades, various investigators have focused on the subject to calculate: (i) the equivalent strut width, and (ii) the number of struts used in the macro-model, i.e., single or multiple struts. In this section, the most commonly referenced strut models in the literature are briefly reviewed.

In 1961, Holmes proposed a simplified equation to calculate the width of diagonal structure (Holmes, 1961)

$$W = {d/3},$$
(1)

where d is the diameter of the infill panel as shown in Fig. 2. In 1962, Smith found that based on experimental data of masonry-infilled steel frames, W/d varies from 0.1 to 0.25 (Smith, 1962). As such, the proposed equation was modified as Eq. (2)

$$W = {d/4}.$$
(2)
Fig. 2
figure 2

Strut model for infill panel in framed structures

Full size image

In 1972, Mainstone proposed Eq. (3) to calculate the width of the diagonal strut, which was obtained based on experimental and analytical results and also was defined as the equivalent diagonal strut (Mainstone, 1972)

$$W = 0.16\left( {\lambda_{1} h_{{{\text{col}}}} } \right)^{ - 0.3} d.$$
(3)

In this equation, hcol is the height of the column and λ1 is defined as Eq. (4)

$$\lambda_{1} = \sqrt[4]{{\frac{{E_{\inf } t_{\inf } \sin 2\theta }}{{4E_{{{\text{fr}}}} I_{{{\text{col}}}} h_{\inf } }}}},$$
(4)

where Einf and Efr are the moduli of elasticity for infill and frame materials, respectively. Icol denotes the second moment of area of the column. tinf and hinf are the thickness of the infill panel or equivalent strut and height of the infill, respectively. θ is the angle shown in Fig. 2.

Liauw and Kwan proposed Eq. (5) as an updated version of Eq. (3) (Liauw & Kwan, 1984):

$$W = 0.95h_{{{\text{col}}}} \cos \theta \left( {\lambda_{1} h_{{{\text{col}}}} } \right)^{ - 0.5} .$$
(5)

As an important source for masonry walls, FEMA 306 (2000) introduced Eq. (6) to calculate the width of the diagonal strut, based on available data in the literature at the time of the study

$$W = 0.175\left( {\lambda_{1} h_{{{\text{col}}}} } \right)^{ - 0.4} d.$$
(6)

In the early 2000s, El-Dakhakhni et al. developed a three-strut macro-model for infilled steel frames (El-Dakhakhni et al., 2003), which resulted in Eq. (7) providing estimation for diagonal struts

$$W = {{\left( {1 - \alpha_{{\text{c}}} } \right)\alpha_{{\text{c}}} h}/{\cos \theta }}.$$
(7)

The parameters of this equation are given in Fig. 3, where in addition to a major diagonal member, two off-diagonal struts were also taken into account to model the behavior of the infill. This simplified model was able to properly predict the inelastic behavior of the frame (due to the development of plastic hinges), and the infill (considering the corner crushing model). Moreover, employing three compressive diagonal struts with the proposed arrangement led to a real distribution of bending moments in analyzing structural members of the infilled frames.

Fig. 3
figure 3

Three-strut macro-model proposed by El-Dakhakhni et al. (2003)

Full size image

Chrysostomou and Asteris studied the in-plane response of infills in 2012 (Chrysostomou & Asteris, 2012). To this end, the required expressions to calculate the stiffness, strength, and deformational capacity of the infills were evaluated for different failure modes using parametric studies. The researchers also proposed a simplified approach to predict the in-plane failure modes of these structures. They calculated the width using Eq. (8)—the parameters of which were already defined—as follows Chrysostomou and Asteris (2012):

$$W = 0.270\left( {\lambda_{1} h_{{{\text{col}}}} } \right)^{ - 0.4} d.$$
(8)

A brief overview of the experimental study

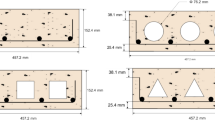
The authors of the present paper published the results of their experimental work on CSP-ISF specimens with various geometrical features and panel-to-frame connections (Hashemi et al., 2018a, 2018b). The large-scale specimens were tested under in-plane lateral cyclic loading according to ATC-24 (1992). The steel frames in the form of intermediate moment-resisting frames were designed in accordance with US national standards AISC 360-10 (2010a) and AISC 341-10 (2010b). Figure 4 shows the beam and column sections and the connection details used in the experimental work with the scale ratio of unity. Figure 5 illustrates the geometric features of the infills as given earlier in Fig. 1. The connection between the infill and the main frame was conducted using L-shaped steel bars (Φ8) spaced at 60 cm. A rigid connection was designed and implemented for the columns’ connections to the base plates, with the rigid connection to the reaction frame having no slippage in any direction. While the cyclic testing, a proper bracing system was in operation to avoid any out-of-plane instability.

Fig. 4
figure 4

a Geometry and dimensions of a CSP-ISF with an aspect ratio of 1.0; b detail of beam-to-column connection for test specimens (dimensions in mm)

Full size image
Fig. 5
figure 5

Detail of CSP used as infill

Full size image

Modeling strategy

DIANA software package (2014) was utilized for finite-element (FE) modeling in this paper. To achieve the designated aims of the study, two models were developed: (i) models using triangular and quadrilateral elements, e.g., using plane stress (micro-model), and (ii) models using line elements, e.g., truss and beam (macro-models). Since the in-plane behavior of the structures was aimed in this study, the two models above were investigated in a 2D design. For the micro-models, the experimental data were used to verify the numerical models. Since it is assumed that the diagonal strut model is evaluated for CSP-ISFs, the macro-models with different diagonal struts, studied in Sec. 2, were evaluated against the experimental and FE results to achieve optimal strut model for CSP infill.

FE modeling using plane stress element

A 4-node quadrilateral isoparametric plane stress element (Q8MEM) was utilized to simulate the frames and the infill. Details of the CSP infill are shown in Fig. 1. In the connection area of the frame to the infill, the boundary conditions were provided through a zero-thickness and 2 + 2 nodes line-interface element (L8IF). An embedded reinforcement element was used in the concrete as steel wire mesh. Since the middle core of the sandwich panel (polystyrene layer) does not affect the structural behavior of the infilled frame, it was excluded from modeling the infill.

To simulate the nonlinear behavior of the shotcrete, a total-strain crack model was employed, which is grounded upon the rotating smeared crack concept available in DIANA. The stress–strain relationship for the compression and tension zones of concrete was assumed as parabolic and exponential functions, respectively (Fig. 6). Based on the theory of Von Mises plasticity, the material behavior of the steel frame was developed as a bilinear stress–strain graph with strain hardening. A combined cracking, shearing, and crushing model—developed by Lourenço and Rots and pre-defined through the software—was determined as an interface element. The input values of the material properties are tabulated in Table 1. The geometry and specifications of the frames are given in Table 2. All details of the models are similar (according to Figs. 4 and 5), except for their aspect ratios.

Fig. 6
figure 6

Stress–strain relationship for shotcrete: a tensile behavior and b compression behavior

Full size image
Table 1 Material properties of CSP-ISF models
Full size table
Table 2 Characteristics of the test specimens and FE models
Full size table

The verification of the models was carried out according to: (i) the consistency of load–displacement graphs (experiments versus numerical results), and (ii) comparative evaluation of the cracking pattern, and stress distribution within the infill panel. One of the objectives of this study is to propose a simplified and practical model for CSP infills; thus, the infilled frame models with different aspect ratios were evaluated under monotonic loading. As presented in Fig. 7, the load–displacement graphs of the FE models are consistent with the experiments in terms of the initial stiffness as well as maximum lateral strength. The Test (+) and Test (−) graphs are associated with the tested specimens in tensile and compressive directions, respectively. Figure 8a shows that the deformation of the frame and the detachment of the infill from the frame for model M (with the aspect ratio of 1.0) subjected to loading were in close agreement with the experimental results. Moreover, the deformed mesh of the infill panel at the compression areas, i.e., upper left and bottom-right corners, is seen in Fig. 8a. This indicates the proper performance of the interface element utilized in the model, which simulated the interaction between the frame and the infill. The cracking pattern and the stress distribution of the infill shown in Fig. 8b, again indicate close consistency between the two methodologies and the diagonal compressive strut formed at the CSP infill is plainly seen.

Fig. 7
figure 7

Load–displacement pushover curves for experimental and FE models

Full size image
Fig. 8
figure 8

Comparison of experimental and numerical results: a deformation of the test specimen and FE model; b cracking pattern (right) and stress distribution (left) within the panel

Full size image

To confirm the robustness and the accuracy of the modeling procedure, the FE model of this study was evaluated against the experimental results of (concrete) sandwich walls available in the literature (Pavese & Bournas, 2011; Ricci et al., 2013b). The walls in these studies had the same specifications as the infill models in the present study (see Fig. 1). Table 3 lists the specifications of the sandwich wall specimens. Two CSP walls (out of four) had a central opening in the form of windows. The reason why the authors decided this was to address the other aim of the study to propose reduction factors used to calculate the initial stiffness and the ultimate strength of the CSP infills with a central opening (see Sec. 5 for more details). The results of the load–displacement curves are shown in Fig. 9, which compares the experimental results to the numerical data. The crack propagation for one of the walls is given in Fig. 10 comparing to the test results, which verifies the numerical results of this research.

Table 3 Description of CSP wall specimens for validation of FE model
Full size table
Fig. 9
figure 9

Load–displacement curves comparing the experimental results to the numerical data

Full size image
Fig. 10
figure 10

Damage pattern of CSP wall (Test 3); distribution of minimum principal stresses (left), crack propagation (mid), and test results (Ricci et al., 2013b) (right)

Full size image

Strut model using line elements

This section addresses the equivalent diagonal strut model—also known as macro-model—in the infilled frames. Comparing the results of the macro-models with existing experiments, the optimal strut model for CSP infills was selected. As listed in Table 4, the cross-section of the struts was calculated based on the existing relations for CSP-ISFs of this study. Through this method, beams and columns are modeled using a ‘beam’ element (CL9BE), while the diagonal struts were modeled through a ‘truss’ element (L2TRU), as shown in Fig. 11. The material properties of the diagonal struts were adopted the same as CSP panels. The thickness of the struts was adopted equal to the thickness of the panels, as described in the FE section above. Prior to modeling the infill, the results of modeling the bare frame, using the ‘beam’ element, were compared with the test results (Fig. 12 shows the load–displacement graph). This assured the authors that the modeling was accurate.

Table 4 Different expressions of the strut model considered in this study
Full size table
Fig. 11
figure 11

Macro-modeling of CSP-ISFs using line elements; a single strut and b three-strut

Full size image
Fig. 12
figure 12

Verification of the bare frame macro-model

Full size image

The results of the macro-modeling of CSP-ISFs with different aspect ratios are shown in Figs. 13, 14 and 15. Having compared the results, it is generally found that three models including Stafford Smith (1962), Liauw and Kwan (1984), and El-Dakhakhni et al. (2003) have a relatively good agreement with experimental results. Among them, the relationship proposed by Liauw and Kwan (1984) gives a more accurate estimate for the stiffness and the strength of all other available formulas. Although the equations given by Mainstone (1972) or FEMA 306 (2000) are mostly used by researchers in the field of masonry-infilled frames, these equations appeared to be not of high accuracy for CSP infills.

Fig. 13
figure 13

Comparison between the test results and strut models for model S (aspect ratio of 0.6)

Full size image
Fig. 14
figure 14

Comparison between the test results and strut models for model M (aspect ratio of 1.0)

Full size image
Fig. 15
figure 15

Comparison between the test results and strut models for model L (aspect ratio of 1.4)

Full size image

It should be noted that, in addition to the method used here, the nonlinear behavior of the infill panel can be simulated by assigning a nonlinear hinge to the diagonal strut, which has been considered by various researchers (Ahmad et al., 2014; Kareem & Pantò, 2019; Van et al., 2022).

Proposed reduction factors for CSP infills with a central opening

According to FE results, a simple analytical method previously proposed to estimate the lateral stiffness and strength of the masonry-infilled frames with a central opening is modified here for the CSP infill. To consider the effect of opening, the effective width of the single strut (We) is modified by multiplying a reduction factor, RF, to the diagonal strut width of a corresponding solid (fully) infilled frame (W) as follows:

$$W_{{\text{e}}} = R_{{\text{F}}} \times W.$$
(9)

There are empirical relationships in the literature to calculate the reduction factor of perforated masonry infill panels. Mohammadi and Nikfar examined their accuracy by collecting the most relevant empirical relationships (Mohammadi & Nikfar, 2013). According to their study, the equation proposed by Al-Chaar et al. (2003) given by Eq. (10) has higher accuracy than other relationships

$$R_{{\text{F}}} = 0.6\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right)^{2} - 1.6\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right) + 1,$$
(10)

where Ao and Ap are, respectively, the opening’s area and the area of the panel.

Based on experimental results available in the literature, Mohammadi and Nikfar (2013) also found that the strength reduction factor is strongly dependent on the frame material (steel or RC), even if previous researchers did not consider it. For this reason, the following two modified formulas were proposed in Mohammadi and Nikfar (2013) as the stiffness and strength reduction factors of the infilled frame with window opening:

$$R_{{\text{K}}} = 1.1859\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right)^{2} - 1.6781\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right) + 1,\;{\text{for}} \frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }} \le 0.40$$
(11)
$$R_{{\text{F}}} = \left\{ \begin{gathered} - 1.085\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right) + 1,\quad {\text{for}}_{{}} \frac{{A_{{\text{o}}} }}{{A_{p} }} \le 0.40\quad {\text{RC frame}} \hfill \\ - 2.122\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right) + 1,\quad {\text{for}}_{{}} \frac{{A_{{\text{o}}} }}{{A_{p} }} \le 0.25\quad {\text{Steel frame}}, \hfill \\ \end{gathered} \right.$$
(12)

where RK and RF are the stiffness and strength reduction factors, respectively.

Based on the numerical method presented in Sect. 4, some CSP-ISF models were developed including central opening with different opening areas (Fig. 16). The lateral stiffness and strength of the models were also calculated using relationships proposed in Mohammadi and Nikfar (2013), Al-Chaar et al., (2003) and their results are given in Fig. 17. As shown, the relationships do not have sufficient accuracy for the CSP infill. Hence, for CSP-ISF with the central window opening, the reduction factors of the stiffness and strength are modified as

$$R_{{\text{K}}} = 1.7\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right)^{2} - 2.3\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right) + 1,\quad {\text{for}}\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }} \le 0.50$$
(13)
$$R_{F} = 1.1\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right)^{2} - 1.15\left( {\frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }}} \right) + 1,\quad {\text{for}} \frac{{A_{{\text{o}}} }}{{A_{{\text{p}}} }} \le 0.50,$$
(14)
Fig. 16
figure 16

Crack propagation (left) and distribution of minimum principal stress (right) in the CSP infill with opening

Full size image
Fig. 17
figure 17

Comparison between the results of the numerical study and the analytical procedures presented in Mohammadi and Nikfar (2013), Al-Chaar et al. (2003)

Full size image

where the parameters are the same as the previous equations. A comparison of the analysis and proposed relationships shows that Eqs. (13) and (14) have an acceptable accuracy in the estimation of the stiffness and strength of the CSP-ISFs with a central opening, as shown in Fig. 18.

Fig. 18
figure 18

Comparison of the results obtained from FE analysis and proposed reduction factor for prediction of lateral stiffness and strength

Full size image

Conclusion

This research aimed to achieve an optimal strut model for concrete sandwich infill panels through finite-element analysis. First, a 2D model was developed using plane stress elements through DIANA software, and the validation of the models was conducted comparing the obtained results with the existing test results. Then, the equivalent diagonal strut model was employed, which is a widely used method in this area for masonry-infilled frames.

The results showed that compared with the other equations, the equation proposed by Liauw and Kwan (1984) provides a closer estimate for stiffness and strength of infilled frames with CSP infills.

A simplified analytical method was proposed to calculate the in-plane stiffness and strength of the CSP-ISFs with a central opening. Reduction factors were proposed, which after multiplying the factors by the width of the equivalent diagonal struts, the initial stiffness and ultimate strength of CSP-ISFs were calculable. It was found that the modified equations used in this study give results with higher accuracy compared to the existing equations in the literature.

As a final remark, due to a limited number of experimental studies on CSP-ISF systems relative to the masonry-infilled, further tests are required especially on (concrete) sandwich panels with an opening. A sizable dataset in this area can definitely help improve the equations and the accuracy of the analytical procedure proposed in this study. In the case of pre-damaged infilled frames, more studies are also required to be conducted on the equivalent strut modeling due to the presence of cracks and changing the mechanical properties of the system (Khan et al., 2020).