Was bedeutet Wachstum? Das ist eine einfache Frage mit einer sehr komplizierten Antwort. Je nach Art des Naturphänomens, das wir modellieren möchten, gibt es verschiedene Möglichkeiten, Wachstum zu beschreiben. Eine sehr mächtige Theorie, die den Wachstumsmechanismus vieler biologischer Systeme (wie die Bildung von Hörnern, Zähnen und Muscheln, das sekundäre Wachstum von Bäumen oder die Zellmotilität aufgrund von Aktin-Wachstum) umfasst, ist die des akkretiven Wachstums, bei dem Körper durch Hinzufügen von Masse an ihren Grenzen wachsen. Akkretives Wachstum ist auch für technologische Anwendungen, wie zum Beispiel Metallbefestigung, Kristallwachstum, 3D-Druck und additive Fertigung, von großer Bedeutung.

Stellen wir uns vor, wir würden eine Muschel über Hunderte oder vielleicht sogar Tausende von Jahren beobachten: Wie könnten wir die Art und Weise, wie die Muschel wächst, mathematisch beschreiben?

Die erste Beobachtung ist, dass die Muschelschale ihre Form während des Wachstums ständig verändert, indem sie weitere Schichten hinzufügt. Eine Strategie zur Beschreibung des zugrundeliegenden Mechanismus besteht darin, jeden Punkt der Muschel zu betrachten, ihre normale Richtung (das heißt die Richtung, die orthogonal zur Oberfläche ist) zu betrachten und im Laufe der Zeit zu prüfen, wie viele neue Schichten dort nacheinander erscheinen. Eine andere ergänzende Möglichkeit, dieses Problem zu betrachten, ist folgende: Wir wählen einen beliebigen Punkt im Raum um die Muschel herum, betrachten ihn über einen sehr langen Zeitraum und verfolgen den genauen Zeitpunkt (falls es einen gibt), an dem der Punkt schließlich Teil der Muschel selbst ist, weil die Muschel so stark gewachsen ist, dass sie diesen Punkt schließlich erreicht und aufgenommen hat.

Kontinuierliche Funktion

Mit anderen (mathematischeren) Worten beschreiben wir das Wachstum eines Festkörpers mithilfe einer sogenannten kontinuierlichen Funktion ϑ, deren Wert an jedem Punkt x die Zeit angibt, an dem der Punkt x dem Festkörper hinzugefügt wird. Dementsprechend können wir folgende Objekte beschreiben:

Wir nennen Ω(0), die Menge der Punkte, die unserem Festkörper zum Zeitpunkt 0 gehören, und Ω(t), die Menge aller Punkte, die unserem Festkörper zum Zeitpunkt t gehören. Der mechanische Zustand des Festkörpers wird dann durch seine Verschiebung u(x,t) beschrieben, die uns sagt, wie jeder Punkt x, der zu Ω(t) gehört, zum Zeitpunkt t im mechanischen Gleichgewicht ist.

Um die Tatsache zu modellieren, dass die Akkretion aus der Ablagerung von neuem Material an der Grenze resultiert, wird für jeden Punkt x(t) auf der Grenze von Ω(t) angenommen, dass er einem normalen Akkretionsgesetz folgt, das heißt, dass sich x(t) immer in seiner normalen Richtung entwickelt. Aus mathematischer Sicht führt dies zur Untersuchung eines Systems von zwei Gleichungen: Eine ist die sogenannte Eikonalgleichung, die uns sagt, wie sich ϑ und damit Ω(t) in der Zeit verändern. Die zweite ist eine Gleichung über u(x,t), die sagt uns, wie sich unser sich entwickelnder Körper mechanisch verhält.

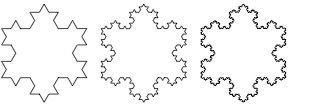
Das Problem besteht darin, dass diese zweite Gleichung sehr schwer zu behandeln ist, da sie auf der Menge Ω(t) basiert, die sich im Laufe der Zeit entwickelt und im Prinzip eine sehr komplizierte Geometrie haben könnte. Eines der ersten Resultate, das zusammen mit dem Mathematiker Ulisse Stefanelli von der Universität Wien bewiesen wurde, ist, dass die Form von Ω(t) zwar kompliziert, aber nicht "super schlecht" sein kann. Tatsächlich haben wir bewiesen, dass der akkretive Wachstumsmechanismus auch keine externen Spitzen erzeugt, wenn wir von einem Satz ausgehen, der keine externen Spitzen aufweist. Mathematisch ausgedrückt haben wir bewiesen, dass unsere Ω(t) sogenannte "John Domains" sind. Andererseits können, selbst wenn unser ursprüngliches Ω(0) relativ schön war und glatte Grenzen hatte, seltsame Dinge passieren und es könnte im Laufe der Zeit eine fraktale Grenze (wie eine Koch-Schneeflocke) entstehen.

Korn-Ungleichung

In der Mathematik gibt es ein sehr leistungsfähiges Werkzeug namens Korn-Ungleichung, das folgendes gewährleistet: Wenn die Menge, in der wir arbeiten, "schön genug" ist, und wenn wir sicher sind, dass Verformungen einen Festkörper nicht zu stark verzerren, dann können diese Verformungen nicht "zu groß" sein und ihre Amplitude wird durch eine Konstante K gesteuert, die von der Form der Menge abhängt. Als wir jedoch versuchten, das steigende Wachstum zu modellieren, mussten wir uns zwei Herausforderungen stellen:

Zusammen mit einem internationalen Team bestehend aus Katerina Nik von der TU Delft, Ulisse Stefanelli von der Universität Wien und Giuseppe Tomassetti von der Universität Rom La Sapienza haben wir bewiesen, dass die oben erwähnte Korn-Ungleichung einheitlich für alle unsere Mengen Ω(t) gilt, und wir haben die Existenz von Lösungen für die mathematische Kopplung von Wachstum und Elastizität nachgewiesen.

Diese Arbeit ist der erste Schritt, um viele weitere komplizierte und interessante Fragen anzugehen: Was wäre, wenn sich ein Material beim Wachsen nicht nur elastisch verformen, sondern auch brechen würde? Könnten wir das Wachstum eines Systems steuern, indem wir beispielsweise bestimmte Parameter vorschreiben, um zum Zeitpunkt t eine bestimmte Konfiguration zu erreichen? Die Beantwortung dieser Fragen könnte nicht nur aus mathematischen Gründen von grundlegender Bedeutung sein, sondern auch für ein besseres Verständnis biologischer und industrieller Wachstumsmechanismen. (Elisa Davoli, 16.5.2024)